| Казахстан |
Опубликован: 23.04.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова
Лекция 3:
Алгоритмы растеризации отрезков, окружностей и эллипсов
3.3. Изображение отрезка с нецелочисленными координатами концов
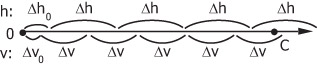
Для отрезка с нецелочисленными координатами концов будем строить соответствующую 4-связную линию на растре.
Существует два подхода.
- Округлить координаты концов до целочисленных и воспользоваться алгоритмом для целочисленного случая. Недостаток: может вызывать существенные искажения (особенно в случае отрезков небольшой длины).
- Перейдем к нашему каноническому случаю, который теперь характеризуется тем, что отрезок лежит в первом октанте, но координаты
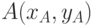 в этом случае:
в этом случае: 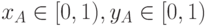 . Параметризуем наш отрезок стандартным образом:
. Параметризуем наш отрезок стандартным образом:![(x, y) = A + t \cdot \frac{B-A}{c}, t \in [0, c],](/sites/default/files/tex_cache/e4f56777a050179d0abb579613b47839.png)
где A и B - концевые точки, c > 0 - некий масштабный коэффициент. Сделаем c достаточно большим целым числом, чтобы уменьшить ошибки округления. Тогда рассмотрим
- приращение t, при сдвиге на 1 пиксель по x ;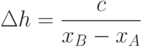 - приращение t, при сдвиге на 1 пиксель по y.
- приращение t, при сдвиге на 1 пиксель по y.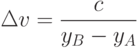
Будем сравнивать текущие значения h и v, а затем, в зависимости от этого, делать шаг по x или y и придавать соответствующие приращения h и v. Алгоритм закончится, когда h или v превысит c.
x = 0; y = 0; // Канонический случай: начальная точка
// лежит в [0, 1) (+) [0, 1)
/* Приращения t, соответствующие смещениям от начальной
точки до границ первого пикселя. */
h = delta_h * (1 - xA); // delta_h0
v = delta_v * (1 - yA); // delta_v0
while( (h < c) AND (v < c) )
{
plot(x, y);
if( h < v )
{
// Сдвиг по горизонтали
x++; h += delta_h;
}
else if( h > v )
{
// Сдвиг по вертикали
y++; v += delta_v;
}
else
{
// h = v : Вырожденный случай (см. рис. 3.5)
// рисуем произвольный из двух возможных пикселей,
// например, верхний:
plot(x,y+1);
x++; y++;
h += delta_h; v += delta_v;
}
}
Листинг
3.4.
Алгоритм отображения отрезка с нецелочисленными координатами концов
Замечание. Приведенный выше алгоритм легко обобщается на n -мерный случай.