Рекурсия

5.2. Функции

В языке Visual Prolog наряду с предикатным стилем можно использовать функции и функциональный стиль программирования. Функции объявляются следующим образом:

class predicates
    имя_функции: (домен1, домен2, …) -> домен_значений.

Например:

class predicates
    f: (real, real) -> real.
clauses
    f(X, Y) = X + Y.

После знака -> стоит имя домена, которому принадлежит значение функции. В правиле это значение определяется после знака равенства. Аргументы функции могут быть как входными, так и выходными. Функция может иметь любой режим детерминизма.

Аналогичное определение функции f из приведенного выше примера в предикатном стиле имеет вид:

class predicates
    f: (real, real, real [out]).
clauses
    f(X, Y, X + Y).

Предикатный домен — это домен, элементами которого являются предикаты. Имена этих предикатов могут быть аргументами предикатов высшего порядка. В объявлении предикатных доменов указываются типы предикатов вместе с режимами детерминизма и потоками параметров. Предикатный домен функций объявляется и используется, например, следующим образом:

domains
    fun = (real, real) -> real.

class predicates
    f : fun.
    g : fun.
clauses
    f(X, Y) = X + Y.
    g(X, Y) = X * Y.

    run():-
        (F = f; F = g),
            R = F(2, 3),
            write(R), nl,
        fail;
        _ = readLine().

В следующих двух программах генерируются натуральные числа в порядке убывания, от заданного числа n до единицы включительно. Например, цель

number(3, X)

имеет следующий набор решений:

X = 3
X = 2
X = 1

Используется сначала предикатный стиль, а затем, для сравнения, функциональный.

class predicates
    number: (positive Граница, positive Число) multi (i,o).
clauses
    number(X, X).
    number(N, X):-
        N > 1,
        number(N - 1, X).

    run():-
        number(3, X),
            write(X), nl,
        fail;
        _ = readLine().

class predicates
    number: (positive) -> positive multi.
clauses
    number(N) = N.
    number(N) = number(N - 1):-
        N > 1.

    run():-
        write(number(3)), nl,
        fail;
        _ = readLine().

Упражнение 2. Напишите генератор натуральных чисел по возрастанию от 1 до заданного числа N.

В следующей программе факториал целых неотрицательных чисел определяется в виде функции, с помощью хвостовой рекурсии.

class predicates
    fact: (positive) -> unsigned64.
    fact: (positive, unsigned64) -> unsigned64.
clauses
    fact(N) = fact(N, 1).

    fact(0, X) = X:- !.
    fact(N, X) = fact(N - 1, N * X).

    run():-
        write(fact(5)),
        _ = readLine().

Используем функции для вычисления чисел Фибоначчи. Последовательность Фибоначчи — это последовательность натуральных чисел, которая определяется следующим образом:

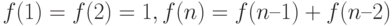для .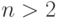

Это определение можно буквально перенести в программу:

class predicates 
    f: (positive) -> unsigned64.
clauses
    f(N) = 1:- N < 3, !.
    f(N) = f(N - 1) + f(N - 2).

Но эта программа уже при n = 40 требует для поиска решения нескольких секунд. Поэтому используем для вычисления n-го числа Фибоначчи хвостовую рекурсию. Для этого будем хранить на каждом шаге рекурсии два соседних элемента последовательности.

class predicates
    fib: (positive) -> unsigned64.
    fib: (positive, unsigned64, unsigned64) -> unsigned64.
clauses
    fib(0) = 0:- !.
    fib(N) = fib(N, 0, 1).

    fib(1, _, Y) = Y:- !.
    fib(N, X, Y) = fib(N - 1, Y, X + Y).

    run():-
        write(fib(70)),
        _ = readLine().

Упражнение 2. Напишите программу, которая по заданному натуральному числу определяет номер наибольшего элемента последовательности Фибоначчи, не превосходящего этого числа.