|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Инструментальные платформы МКМД-бит-потоковых вычислительных технологий
Инструментальное средство MatrixDesigner реализовано в среде Microsoft Visual Studio 2005 и написано на языке C#.
На выбор типа преобразований, обеспечивающих в квазиреальном масштабе времени парирование действующей в бит-матрице карты отказов, решающее влияние оказывают два фактора:
- МКМД-бит-потоковая технология, как и любая синхронная конвейерная или систолическая технология, критична к нарушениям даже на 1 такт требуемых фазовых соотношений между потоками данных, поступающими на входы каждого бит-процессора из сверх- или гипербольшого коллектива;
- централизованная система резервирования обеспечивает максимальное использование структурно-функциональных возможностей всей системы, если средства коммутации и средства управления коммутацией обеспечивают дифференцированное, полнодоступное "перемещение" по всей рабочей области матрицы любого бит-процессора из существенно меньшего по площади "горячего" аппаратного резерва. При наличии отказов формализованный синтез критичной к фазовым сдвигам топологической схемы поток-оператора пользователя усугубляется еще и тем, что в этом случае приходится искать практически индивидуальное решение на каждую систему ограничений из гиперкомбинаторного пространства, генерируемого допустимыми в бит-матрице картами частичных или полных отказов бит-процессоров.
В технике подобного рода задачи обычно решаются адаптивными методами, по максимуму сохраняющими критичные характеристики исходной "сложной" системы, затрагиваемые используемыми в процессе адаптации преобразованиями.
Описанным условиям и динамическим требованиям в достаточной мере удовлетворяют локальные и глобальные аффинные преобразования "рабочего тела" тестовых или пользовательских микропрограмм. В этом случае:
- исходным объектом преобразований служит топологическая схема микропрограммы, полученная дорогостоящим эмпирическим путем;
- полностью сохраняются фазовые соотношения между пространственно-временными потоками данных внутри преобразуемых микропрограммных модулей;
- для восстановления информационных связей и фазовых соотношений по потокам данных между перемещаемыми и неподвижными микропрограммными модулями используются бит-процессоры, способные выполнить требуемые коммутационные функции. Аффинные преобразования в геометрии сохраняют линейные соотношения между объектами преобразований, а при их использовании в системе парирования отказов и при проектировании МКМД-бит-процессорных матриц, кроме преобразования координат, размещения бит-операций на матрице, в ряде случаев требуют еще и преобразования содержимого адресной части перемещаемых по бит-матрице микропрограммных модулей.
Рассмотрим преобразования координат размещения бит-команд в поток-операторе пользователя (бит-процессорном устройстве). Здесь  и
и  - координаты бит-процессора. В общем случае его координаты после проведения аффинных преобразований изменятся на
- координаты бит-процессора. В общем случае его координаты после проведения аффинных преобразований изменятся на 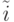 и
и 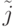 ,
, 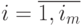 ,
, 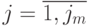 . Алгоритмы вычисления нового положения каждого бит-процессора:
. Алгоритмы вычисления нового положения каждого бит-процессора:
- Поворот на +90o:
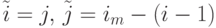 .
. - Поворот на -90o:
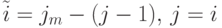 .
. - Вращение вдоль оси Х:
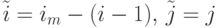 .
. - Вращение вдоль оси Y:
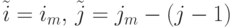 .
. - Вращение вдоль главной диагонали:

- Вращение вдоль побочной диагонали:
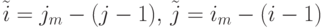 .
.
В каждом из рассмотренных выше случаев аффинных преобразований есть необходимость изменения содержимого регистра каждого бит-процессора. Преобразование кодов бит-команд производится следующим образом (  - регистр бит-процессора,
- регистр бит-процессора,  - значение регистра бит-процессора после преобразования):
- значение регистра бит-процессора после преобразования):
- Поворот на +90o:
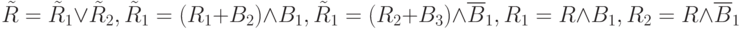
где
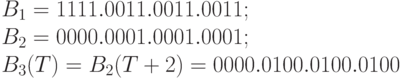 .
. -
2. Поворот на -90o: то же, что и на +90o, только
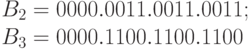 .
. - Вращение вдоль оси Х:
 ,
где
,
где 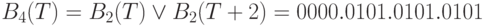 .
. - Вращение вдоль оси Y:
 .
. - Вращение вдоль главной диагонали:
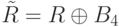 .
. - Вращение вдоль побочной диагонали:
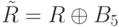 , где
, где 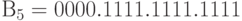 .
.
Входы и выходы устройства в нотации MatrixDesigner изображаются в виде треугольников. Порт устройства является объектом, свойство которого пользователь может увидеть в таблице свойств выбранного объекта. Чтобы обеспечить эту возможность, необходим алгоритм определения принадлежности точки треугольнику. На вход такого алгоритма подаются координаты вершин треугольника в прямоугольной системе координат и координаты точки, а выходом алгоритма является логическое значение true, если точка принадлежит треугольнику, и false, если точка лежит за пределами треугольника. Эту проверку осуществляет метод Triangle::IsPointInTriangle. Алгоритм следующий:
- Если тестируемая точка совпадает с одной из вершин треугольника, вернуть true, иначе перейти к пункту 2.
- Найти уравнение прямой для произвольной стороны треугольника (вершины P 1 и P 2) L 1.
- Найти уравнение прямой для отрезка между вершиной треугольника, которая не принадлежит L 1 ( P 3), и точкой, где щелкнула мышь ( P 4)( L 2).
- Найти точку пересечения L 1 и L 2 ( P 5). Если прямые параллельны, вернуть false, иначе перейти к пункту 5.
- Найти расстояния между P 1 и P 2, между P 1 и P 5 и между P 2 и P 5 и, используя неравенство треугольника, проверить, что точка P 5 лежит на отрезке от P 1 до P 2. Если проверка успешна, перейти к пункту 6, иначе вернуть false.
- Найти расстояния между P 3 и P 5, между P 3 и P 4 и между P 5 и P 4. Аналогично, используя неравенство треугольника, проверить, что проверяемая точка лежит на отрезке от P 3 до P 5. Если это условие выполняется, то точка лежит внутри треугольника (вернуть true ), иначе вернуть false.
Одной из наиболее сложных задач в плане программной реализации является создание пользовательского интерфейса, особенно той его части, которая отвечает за визуальное отображение данных проекта (бит-матрица и находящиеся на ней операционные устройства) и работу с ним. Чтобы отделить реализацию этого элемента пользовательского интерфейса от создания других частей программы, модуль рисования и работы над бит-матрицей оформлен в виде пользовательского элемента управления ( UserControl ) и реализован в классе MatrixDirectDrawView. Именно в нем реализованы методы копирования и вставки объектов, методы рисования данных проекта на экране, а также методы взаимодействия программы с пользователем посредством клавиатуры и мыши. Особого внимания заслуживает алгоритм перерисовки проекта. Входными данными здесь являются процессорная матрица, ее размер, находящиеся на ней операционные устройства, текущий масштаб, положение полос прокрутки. Алгоритм рисования проекта в любой момент времени:
- 1 Рассчитать, какие бит-процессоры из бит-матрицы будут видны на экране.
- Заполнить матрицу цветом фона.
- Найти смещение сетки бит-процессоров от левого верхнего угла элемента управления.
- С помощью данных, полученных на шаге 1, найти список операционных устройств, которые видны на экране.
- Для каждого устройства из списка выполнить процедуру рисования. Она заключается в изображении прямоугольника (цвет которого определяется устройством), и рисовании портов (входов и выходов).
- Нарисовать сетку бит-процессоров.
- Если есть устройства, выбранные пользователем, то нарисовать рамку выделения вокруг них.
- Нарисовать курсор вставки.
Важным является алгоритм определения номера устройства, на которое щелкнула мышь. Чтобы реализовать эту задачу наиболее просто
и быстро, применен следующий подход. Создается таблица размещения устройств ( Location Table ), которая представляет собой двумерный массив целых чисел, размер которого равен размеру бит-матрицы в бит-процессорах. Значение каждого элемента массива с координатами [i, j] равно номеру процессорного устройства в списке процессорных устройств матрицы, которое "перекрывает" позицию [i, j]. Если несколько устройств перекрывают позицию [i, j] (то есть устройства накладываются друг на друга), то значение элемента таблицы размещения устройств равно большему номеру устройства. Если ни одно устройство не находится в указанной позиции, то Location Table[i, j] равно минус один. Таким образом, когда пользователь щелкает мышью, программа определяет позицию бит-процессора, на который указал пользователь, и по значению элемента из таблицы размещения устройств находит номер выбранного устройства (или определяет факт того, что щелчок пришелся по "незанятой" части бит-матрицы).
