Самостоятельная работа 7: Оптимизация и распараллеливание вычислений в задаче детектирования объектов на изображениях с использованием алгоритма Latent SVM

12. Приложения

12.1. Приложение А. Обобщенный метод преобразования расстояний для решения задачи оптимизации

12.1.1. Постановка задачи

В некоторых случаях полезно иметь карту свойств, которая определяет вес (стоимость) свойства для пикселя, а не отсутствие или наличие этого свойства в каждом пикселе. Как следствие, преобразование расстояний должно зависеть от расстояния между пикселями и веса свойства.

Пусть – регулярная решетка, а 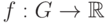- функция, заданная на этой решетке и определяющая вес свойства. Определим преобразование расстояний следующим образом:

где 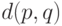– расстояние между точками p и q (расстояние, в частности, может выражаться евклидовой метрикой). Таким образом, данное преобразование для каждой точки p определяет ближайшую точку q , в которой функция f принимает достаточно маленькое значение (очевидно, что оно не обязательно является минимальным).

В большинстве алгоритмов преобразования расстояний функция весов f вводится как индикаторная функция :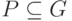

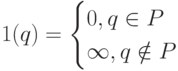
Как следствие, минимизация проводится не на всей сетке, а некотором выделенном подмножестве .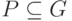

12.1.2. Решение задачи в случае евклидова расстояния на одномерной сетке

Предположим, что построена одномерная сетка 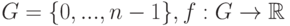- произвольная функция, заданная на этой сетке. Тогда задача преобразования расстояний имеет вид:

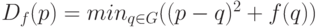
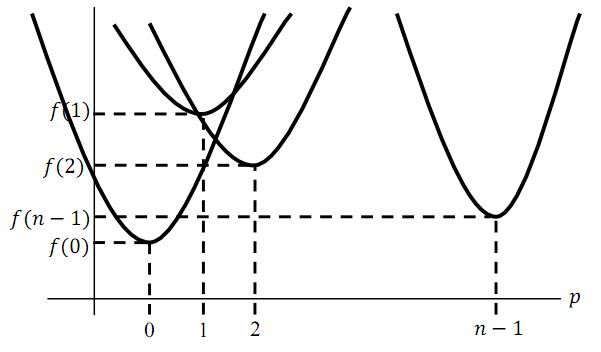
Необходимо отметить, что минимизируемая функция представляет собой параболу с вершиной в точке 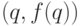при всех значениях q, ветви которой направлены вверх. Поэтому при всех значениях 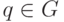получаем совокупность таких парабол. Как следствие, преобразование расстояний – это высота нижней огибающей указанного множества парабол.

Рис. 14.3.

Алгоритм вычисления преобразования состоит из двух этапов:

1. Построение нижней огибающей для парабол, соответствующих каждой точке регулярной сетки.

Замечания к алгоритму:

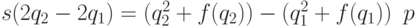
• Любые две параболы из построенной совокупности пересекаются ровно в одной точке. Пусть и – пара точек, принадлежащих сетке . Рассмотрим точку пересечения s парабол, абсциссы вершин которых совпадают с указанными точкам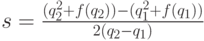и: Если 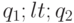, то точка лежит левее точки пересечения.
• На каждой итерации алгоритма рассматривается очередная парабола и строится огибающая для расширенного множества парабол.

Обозначения:

k – количество парабол, которые включены в состав огибающей на текущем шаге алгоритма.

– значение абсциссы вершины k-ой параболы,

– отрезок, в котором ая парабола лежит ниже -ой и некоторой текущей параболы.

Описание алгоритма:

Для каждой параболы с абсциссой вершины q из множества, заданного на сетке, выполняется следующая последовательность действий:

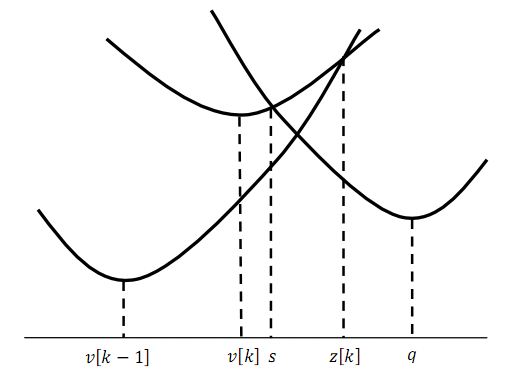
• Определяется абсцисса s точки пересечения текущей параболы и k-ой параболы, которая была последней включена во множество, образующее огибающую.
• Если точка пересечения оказалась меньше (или равна) левой границы , то последняя парабола не принадлежит огибающей и ее необходимо исключить из множества.
  

  
  Рис. 14.4.
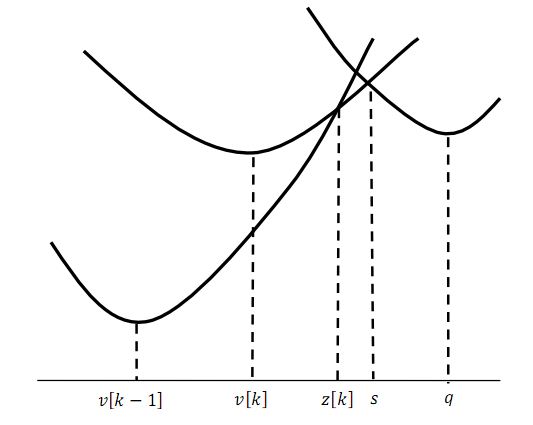
• В противном случае, текущую параболу необходимо включить во множество (запомнить абсциссу вершины этой параболы и левую границу отрезка, на котором она ниже предшествующей параболы, т.е. вычисленную точку пересечения).
  

  
  Рис. 14.5.

2. Определение значений 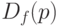в каждом положении p, принадлежащем сетке:

• Определение номера отрезка, которому принадлежит точка p.
• Вычисление значения преобразования:

Рис. 14.6.

12.1.3. Решение задачи в случае евклидова расстояния на двумерной сетке

Предположим, что построена двумерная сетка 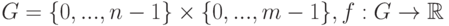– произвольная функция, заданная на этой сетке. Тогда преобразование расстояний имеет вид:

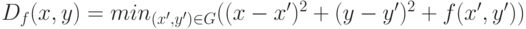
Данная задача приводится к более простой, т.к. первое слагаемое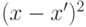 минимизируемой функции не зависит от :

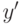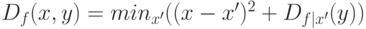
где 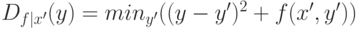– задача преобразования расстояний на одномерной сетке при каждом фиксированном . Таким образом, необходимо решить n задач на одномерной сетке.

В случае произвольного вектора 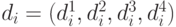получаем квадратичную функцию:

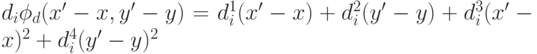
Решение такой задачи отличается от рассмотренной только способом вычисления вершины параболы и точки пересечения пары парабол.