Проективная геометрия в компьютерном зрении

1.7. Стерео-зрение

До сих пор мы в основном обсуждали, что у нас получается, если есть только одно изображение. Сейчас мы детально поговорим о математических моделях для случая, когда у нас есть два изображения одной и той же сцены: какая здесь есть геометрия и что нам это дает. На самом деле получается, что если у нас есть два изображения сцены, то мы сможем восстановить трехмерную структуру. Имея только одно изображение, мы можем сказать лишь, что пиксель соответствует какой-то трехмерной точке на луче, проходящем через этот пиксель. Если же у нас есть второе изображение, то мы сможем точно установить трехмерные координаты этой точки.

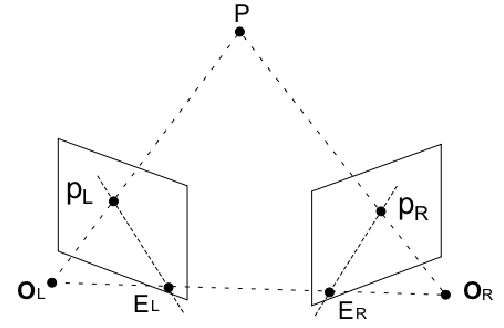
Пусть у нас есть две камеры:

Рис. 5.17. Epipolar Geometry, Wikipedia

левая и правая, при этом они немного повернуты друг относительно друга. Пусть мы знаем плоскости первой и второй камер. Пусть есть какая-то трехмерная точка, которую мы наблюдаем. Тогда для первой камеры она спроецируется по лучу, как и было раньше, а для второй камеры она спроецируется по другому лучу. Мы знаем координаты 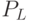– на левом изображении, и нас интересует вопрос, где на правом изображении может располагаться проекция этой точки, то есть вопрос о нахождении соответствующей точки. Легко сообразить, что здесь получается. По 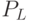мы понимаем, на каком луче она находится, соответственно на правом изображении она находится на проекции этого луча. Проецируем луч на правое изображение и получаем некую прямую. И на этой прямой находится искомая проекция точки P. Мы получили эпиполярную линию – это та линия, на которой может находиться соответствующая точка. Раньше, когда мы рассматривали соответствия, мы брали точку на одном изображении, брали второе изображение и искали по всему изображению, где же может находиться соответствующая точка. Когда у нас две камеры смотрят на одну и ту же сцену, у нас получается, что соответствующая точка будет находиться не на всем изображении – она находится всего лишь на одной линии – эпиполярной линии. Понятно, что всегда есть шумы, поэтому точка будет не в точности на этой линии, а на небольшом расстоянии. Заметим, что если мы рассмотрим какую-то другую точку и опять спроецируем луч, то проекция вновь пройдет через точку 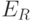. Все лучи проходят через эту точку – проекция центра другой камеры (левой). Соответственно все прямые, при проекции, будут проходить через проекцию центра левой камеры на правом изображении. Такая же ситуация будет при проецировании точек с правой камеры на левую. Тоже будут свои эпиполярные линии, и тоже будет общая точка всех эпиполярных линий – она называется эпиполь.

Это преобразование (закон) можно записать с помощью фундаментальной матрицы:

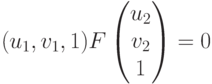
Здесь 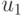, 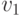– координаты точки на одном изображении: 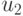, 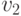– проекции той же трехмерной точки, но на другое изображение.

Если нам удобно работать не в координатах-пикселях, а в трехмерных координатах – (X,Y,Z), то вводится так называемая существенная матрица:

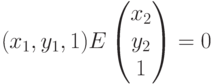
где 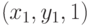– нормированные трехмерные координаты, то есть , .

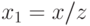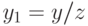Возникает вопрос, как находить фундаментальную матрицу? Ответ следующий: если у нас есть много соответствий между двумя изображениями, то фундаментальная матрица – это такая матрица размерности , которая удовлетворяет соотношению

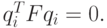
Если мы запишем несколько таких уравнений и решим систему, то мы найдем фундаментальную матрицу. Поскольку фундаментальная матрица определена с точностью до умножения на константу, то восьми соответствий будет достаточно.

Есть еще несколько деталей – ранг матрицы F равен двум. Поэтому чтобы получить матрицу ранга 2, мы заменяем полученное решение на сингулярную матрицу, используя SVD.

Если в уравнении мы зафиксируем u2, v2 и матрицу F, то получим уравнение эпиполярной линии. Если же в уравнение подставить координаты эпиполя – то это будет как раз вырожденный случай.

Если мы знаем, как именно в пространстве расположены камеры относительно друг друга и если мы знаем, как они откалиброваны, то есть мы знаем их внутренние параметры, тогда мы можем написать формулу, по которой матрица F будет вычисляться. Если же камеры не откалиброваны, у нас просто есть изображения с камеры, то по этому пути мы уже не сможем пойти, и фундаментальную матрицу нужно находить через соответствия, как описывалось раньше.

По соответствиям мы можем вычислить фундаментальную матрицу и, как и раньше, мы можем использовать это для геометрической валидации. Как в случае на плоскости, когда мы хотели найти плоский объект, мы пользовались матрицей гомографии. Но если мы хотим найти неплоский объект, то матрица гомографии нам уже не поможет. Но нам поможет фундаментальная матрица. Когда у нас получается много соответствий по дескрипторам и, в том числе, ложных, мы можем проверить для соответствия выполнение уравнения с фундаментальной матрицей. Если для соответствия произведение не обращается в ноль, то следовательно, оно является ложным. И запуская геометрическую валидацию, мы сможем отбросить ложные соответствия и найти произвольный жeсткий объект.

Обсудим, как по двум изображениям можно восстанавливать трехмерные координаты точек. Примерно также работает человеческое зрение: у нас есть два глаза, соответственно, у нас есть два изображения одной и той же сцены. И используя два изображения одной и той же сцены, мы можем восстановить трехмерную структуру. Рассмотрим, в чем состоит идея. Вот у нас есть две камеры, которые смотрят на одну и ту же точку. Мы знаем пиксель проекции с первой камеры и пиксель проекции со второй камеры. Если мы пересечем лучи, на которых эти пиксели лежат, то их пересечение и является рассматриваемой трехмерной точкой. Проблема в том, что когда мы будем искать соответствия, то нам нужно искать соответствия вдоль эпиполярных линий. Эти эпиполярные линии, вообще говоря, расположены как-то под углом, что не очень удобно. Но есть особый случай. Если у нас камеры параллельны друг другу, то эпиполярные линии будут горизонтальные. Если мы попытаемся в таком расположении спроецировать центр второй камеры на изображение, то он у нас не спроецируется, потому что у нас луч из первой камеры и из второй камеры – не пересекутся - так как они параллельны. То есть, по сути точка проецируется в бесконечность, эпиполь у нас находится в бесконечности и эпиполярные линии пересекаются в бесконечности. То есть они все параллельны друг другу, и можно сообразить, что они будут именно горизонтальны. Поэтому для восстановления трехмерной структуры сцены мы будем применять такое преобразование, которое сведет нашу произвольную задачу к этому особому случаю и переведет произвольные эпиполярные линии в горизонтальные.

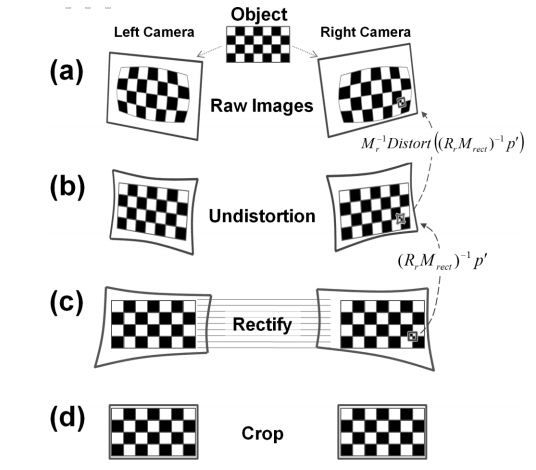
Итак, у нас есть камеры в произвольном положении, которые могут быть повернуты относительно друг друга. Сначала мы строим преобразование обратное к преобразованию дисторсии. То есть из искривленного изображения получаем неискривленное.

Рис. 5.18. Stereo rectification (G. Bradski, A. Kaehler, Learning OpenCV)

Прямые линии они слева в b изогнуты, а после преобразования становятся действительно прямыми. И теперь для неискаженного изображения мы поворачиваем камеры таким образом, чтобы они стали параллельны друг другу – выполняем стерео-ректификацию. После этого соответствующие друг другу точки (в ректифицированном изображении) теперь находятся на одной линии.

Рис. 5.19. Stereo rectification (G. Bradski, A. Kaehler, Learning OpenCV)

И теперь прямые линии соответствуют в точности прямым. И находить соответствия теперь гораздо проще.

Теперь, когда есть два выровненных изображения, полученных относительно друг друга просто сдвигом, можно находить соответствия.

Рис. 5.20. Example of stereo data (University of Tsukuba)

Пусть есть точка на изображении, у нее есть какая-то окрестность. И нам нужно найти соответствующую точку на другом изображении, причем уже не на всем изображении, а просто на горизонтальной линии.

Рис. 5.21.

То есть мы получаем какую-то полоску пикселей и находим такое место, которое наиболее похоже на то, что было у нас раньше:

Рис. 5.22.

Для этого можно просто посчитать евклидово расстояние – сумму квадратов ошибок в каждом пикселе – для какого-то текущего положения. Потому что мы взяли участок – положили его в какое-то место на нашей полоске, посчитали ошибку, запомнили, сдвинули – посчитали следующую ошибку и так далее. В результате мы найдем то место, где ошибка достигает минимума. Таким образом, мы найдем, так называемое, смещение (disparity) для этой точки. И зная смещение, мы уже сможем восстановить трехмерные координаты. Шаблон – это некоторая окрестность 8*8 или 16*16.

Получается, что для точек, которые расположены близко к камерам, это смещение будет большое. Вы рассмотрели изображение с одного места, потом передвинулись, рассматриваете изображение из другого места. Если объект у вас располагался близко, то его координаты сместятся очень сильно. А тот объект, который был у вас далеко – например, гора на заднем фоне – он останется примерно на том же самом месте. Соответственно, это смещение как раз показывает, насколько близко расположен объект. Из подобия треугольников можно вывести формулу. Если известно расстояние между камерами - D, известны внутренние параметры fx, то можно найти уже трехмерную координату Z:

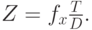
Формула показывает следующее: чем больше смещение, тем ближе точка к нам находится.

Рассмотрим изображение.

Рис. 5.23.

И карта смещения для него

Рис. 5.24.

Светлым показаны области с большим смещением, а темным – со смещением поменьше. И видим, что лампа к нам ближе всех, за ней голова, и потом уже идет какой-то фон.

Используя этот принцип и карту смещения, мы можем корректно восстановить трехмерную структуру нашей сцены. По этому же принципу работает и наше зрение.

1.8. Функции в OpenCV

Все, что мы обсуждали – все это есть в OpenCV в модуле calib3d.

Если у вас есть трехмерные точки, параметры камеры и поза объекта, то используя функцию projectPoints вы можете получить точки на изображении в пикселях.

solvePnP – это решение проблемы PnP – по заданным соответствиям и параметрам камеры найти позу объекта.

calibrateCamera – Калибрация камеры – если у вас есть много изображений шахматной доски, то вы сможете найти ее и откалибровать камеру по найденному шаблону.

Также есть функции для работы с двумя камерами. Эти функции позволяют находить гомографию, фундаментальную матрицу, калибровать две камеры вместе, делать ректификацию и т.п.