|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Основы теории измерений
Средние величины в порядковой шкале
Рассмотрим обработку мнений экспертов, измеренных в порядковой шкале. Справедливо следующее утверждение.
Теорема 1. Из всех средних по Коши допустимыми средними в порядковой шкале являются только члены вариационного ряда (порядковые статистики) .
Теорема 1 справедлива при условии, что среднее  является непрерывной (по совокупности переменных) и симметрической функцией. Последнее означает, что при перестановке аргументов значение функции
является непрерывной (по совокупности переменных) и симметрической функцией. Последнее означает, что при перестановке аргументов значение функции  не меняется. Это условие является вполне естественным, ибо среднюю величину мы находим для совокупности (множества) , а не для последовательности. Множество не меняется в зависимости от того, в какой последовательности мы перечисляем его элементы.
не меняется. Это условие является вполне естественным, ибо среднюю величину мы находим для совокупности (множества) , а не для последовательности. Множество не меняется в зависимости от того, в какой последовательности мы перечисляем его элементы.
Согласно теореме 1 в качестве среднего для данных, измеренных в порядковой шкале, можно использовать, в частности, медиану (при нечетном объеме выборки). При четном же объеме целесообразно применять один из двух центральных членов вариационного ряда - как их иногда называют, левую медиану или правую медиану. Моду, максимум, минимум, квартили тоже можно использовать - они всегда являются членами вариационного ряда. Но никогда нельзя разрабатывать управленческое решение на основе среднего арифметического или среднего геометрического.
Приведем численный пример, показывающий некорректность использования среднего арифметического  в порядковой шкале. Пусть
в порядковой шкале. Пусть 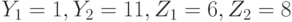 . Тогда
. Тогда 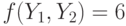 , что меньше, чем
, что меньше, чем  . Пусть строго возрастающее преобразование g таково, что
. Пусть строго возрастающее преобразование g таково, что 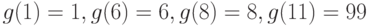 . Таких преобразований много. Например, можно положить
. Таких преобразований много. Например, можно положить 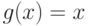 при
при 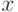 , не превосходящих 8, и
, не превосходящих 8, и 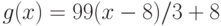 для
для  , больших 8. Тогда
, больших 8. Тогда 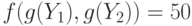 , что больше, чем
, что больше, чем 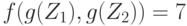 . Как видим, в результате допустимого, т.е. строго возрастающего преобразования шкалы упорядоченность средних величин изменилась.
. Как видим, в результате допустимого, т.е. строго возрастающего преобразования шкалы упорядоченность средних величин изменилась.
Таким образом, теория измерений выносит жесткий приговор среднему арифметическому - использовать его в порядковой шкале нельзя. Однако же те, кто не знает теории измерений, используют его. Всегда ли они ошибаются? Оказывается, можно в какой-то мере (но отнюдь не полностью!) реабилитировать среднее арифметическое, если перейти к вероятностной постановке и к тому же удовлетвориться результатами для больших объемов выборок. В монографии получено также следующее утверждение.
Теорема 2. Пусть  - независимые одинаково распределенные случайные величины с функцией распределения
- независимые одинаково распределенные случайные величины с функцией распределения 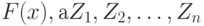 - независимые одинаково распределенные случайные величины с функцией распределения
- независимые одинаково распределенные случайные величины с функцией распределения 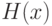 , причем выборки
, причем выборки 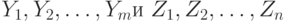 независимы между собой и
независимы между собой и 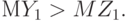 Для того, чтобы вероятность события
Для того, чтобы вероятность события
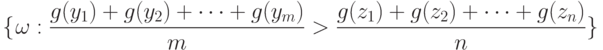
стремилась к 1 при 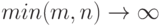 для любой строго возрастающей непрерывной функции g, удовлетворяющей условию
для любой строго возрастающей непрерывной функции g, удовлетворяющей условию
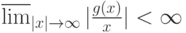
необходимо и достаточно, чтобы при всех x выполнялось неравенство  , причем существовало число x0, для которого
, причем существовало число x0, для которого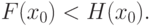
Примечание. Условие с верхним пределом носит чисто внутриматематический характер. Фактически функция  - произвольное допустимое преобразование в порядковой шкале.
- произвольное допустимое преобразование в порядковой шкале.
Согласно теореме 2 средним арифметическим можно пользоваться и в порядковой шкале, если сравниваются выборки из двух распределений, удовлетворяющих приведенному в теореме неравенству. Проще говоря, одна из функций распределения должна всегда лежать над другой. Функции распределения не могут пересекаться, им разрешается только касаться друг друга. Это условие выполнено, например, если функции распределения отличаются только сдвигом, т.е.

при некотором 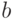 . Последнее условие выполняется, если два значения некоторой величины измеряются с помощью одного и того же средства измерения, у которого распределение погрешностей не меняется при переходе от измерения одного значения рассматриваемой величины к измерению другого.
. Последнее условие выполняется, если два значения некоторой величины измеряются с помощью одного и того же средства измерения, у которого распределение погрешностей не меняется при переходе от измерения одного значения рассматриваемой величины к измерению другого.
Средние по Колмогорову
Естественная система аксиом (требований к средним величинам) приводит к так называемым ассоциативным средним. Их общий вид нашел в 1930 г. А.Н.Колмогоров. Теперь их называют "средними по Колмогорову".
Для чисел 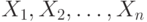 среднее по Колмогорову вычисляется по формуле
среднее по Колмогорову вычисляется по формуле
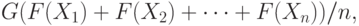
где F - строго монотонная функция (т.е. строго возрастающая или строго убывающая), G - функция, обратная к F.
Среди средних по Колмогорову - много хорошо известных персонажей. Так, если 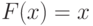 , то среднее по Колмогорову - это среднее арифметическое, если
, то среднее по Колмогорову - это среднее арифметическое, если  , то среднее геометрическое, если
, то среднее геометрическое, если  , то среднее гармоническое, если
, то среднее гармоническое, если 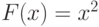 , то среднее квадратическое, и т.д. (в последних трех случаях усредняются положительные величины).
, то среднее квадратическое, и т.д. (в последних трех случаях усредняются положительные величины).
Среднее по Колмогорову - частный случай среднего по Коши. С другой стороны, такие популярные средние, как медиана и мода, нельзя представить в виде средних по Колмогорову. В монографии доказаны следующие утверждения.
Теорема 3. При справедливости некоторых внутриматематических условий регулярности в шкале интервалов из всех средних по Колмогорову допустимым является только среднее арифметическое.
Таким образом, среднее геометрическое или среднее квадратическое температур (в шкале Цельсия), потенциальных энергий или координат точек не имеют смысла. В качестве среднего надо применять среднее арифметическое. А также можно использовать медиану или моду - они не входят в число средних по Колмогорову.
Теорема 4. При справедливости некоторых внутриматематических условий регулярности в шкале отношений из всех средних по Колмогорову допустимыми являются только степенные средние с 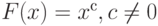 , и среднее геометрическое.
, и среднее геометрическое.
Есть ли средние по Колмогорову, которыми нельзя пользоваться в шкале отношений? Конечно, есть. Например, с 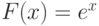 .
.
Замечание 1. Среднее геометрическое является пределом степенных средних при 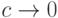
Аналогично средним величинам могут быть изучены и другие статистические характеристики - показатели разброса, связи, расстояния и др. Нетрудно показать, например, что коэффициент корреляции не меняется при любом допустимом преобразовании в шкале интервалов, как и отношение дисперсий. Дисперсия не меняется в шкале разностей, коэффициент вариации - в шкале отношений, и т.д.
Приведенные выше результаты о средних величинах широко применяются, причем не только в теории принятия решений, но и в экономике, менеджменте, экспертных исследованиях, социологии, инженерном деле. Например, для анализа методов агрегирования датчиков в АСУ ТП (автоматизированных системах управления технологическими процессами) доменных печей. Велико прикладное значение теории измерений в задачах стандартизации и управления качеством, в частности, в квалиметрии. Здесь есть и интересные теоретические результаты. Так, например, любое изменение коэффициентов весомости единичных показателей качества продукции приводит к изменению упорядочения изделий по средневзвешенному показателю (эта теорема доказана проф. В.В. Подиновским).
При подготовке и принятии решений необходимо использовать только инвариантные алгоритмы обработки данных. В настоящей главе показано, что требование инвариантности выделяет из многих алгоритмов усреднения лишь некоторые, соответствующие используемым шкалам измерения. Инвариантные алгоритмы в общем случае рассматриваются в математической теории измерений. Нацеленное на прикладные исследования изложение теории измерений дается в монографиях .
Контрольные вопросы
- Всегда ли имеет смысл складывать числа, используемые в той или иной области человеческой деятельности?
- Приведите примеры величин, измеренных в шкале наименований.
- Приведите примеры величин, измеренных в порядковой шкале.
- Приведите примеры величин, измеренных в шкале интервалов.
- Приведите примеры величин, измеренных в шкале отношений.
- Постройте пример, показывающий некорректность использования среднего арифметического
 в порядковой шкале, используя допустимое преобразование
в порядковой шкале, используя допустимое преобразование  (при положительных усредняемых величинах
(при положительных усредняемых величинах  ).
). - Постройте пример, показывающий некорректность использования среднего геометрического в порядковой шкале.
- Какие средние величины целесообразно использовать при расчете средней заработной платы (или среднего дохода)?
Темы докладов, рефератов, исследовательских работ
- Теория измерений как научная дисциплина, посвященная гомоморфизмам эмпирических систем с отношениями в числовые системы с отношениями.
- Показатели разброса, связи, показатели различия (в том числе метрики) в порядковой шкале.
- Ранговые методы математической статистики как инвариантные методы анализа порядковых данных.
- Показатели разброса, связи, показатели различия (в том числе метрики) в шкале интервалов.
- Показатели разброса, связи, показатели различия (в том числе метрики) в шкале отношений.
- Теорема В.В. Подиновского: любое изменение коэффициентов весомости единичных показателей качества продукции приводит к изменению упорядочения изделий по средневзвешенному показателю (доказательство и прикладное значение)

