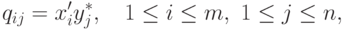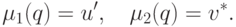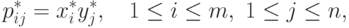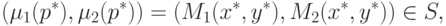Принципы формирования сделки (аксиомы Нэша)
Перейдем к обсуждению условий, определяющих выбор сторонами конкретного
варианта сделки (u,v) из множества S (или выбор
рулетки p из (14.2),
порождающей этот вариант). Конкретные условия, которые мы рассмотрим, были
предложены Дж.Нэшем (см.
"Устойчивость и эффективность поведения сторон: совместимость свойств устойчивости и эффективности"
).
Поэтому их обычно называют аксиомами
Нэша.
При всей специфике взаимодействий участников конкретной операции,
согласующих взаимоприемлемый вариант сделки, можно выделить некоторые
общие моменты, обычно присущие таким взаимодействиям. Согласно Нэшу,
они состоят в следующем.
Участник P1 своими односторонними действиями (т.е. без
кооперации с участником P2 ) может гарантировать себе
математическое ожидание выигрыша, равное величине
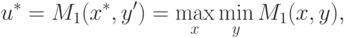 |
(
14.7)
|
где
M1(x,y) из (11.16), (11.17),
а
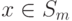
и
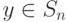
есть смешанные стратегии,
независимо используемые сторонами. Т.е. при оценке гарантированного
уровня мы исходим из того, что сторона
P2 может вести себя как
противник стороны
P1 в антагонистической игре
с матрицей
A, характеризующей интересы
P1. При
таком поведении стороны
P2 ее ожидаемый выигрыш есть величина
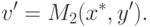 |
(
14.8)
|
При этом пара
(u*,v') принадлежит множеству
S,
поскольку рулетка
p из (14.2), имеющая компоненты
обеспечивает выполнение равенств
ср. (11.16) и (14.3), (14.7).
Кроме того, согласно (14.7),
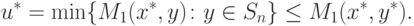 |
(
14.9)
|
Аналогично сторона P2 (также своими односторонними действиями)
может гарантировать себе ожидаемый выигрыш
 |
(
14.10)
|
При этом
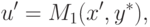 |
(
14.11)
|
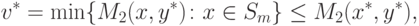 |
(
14.12)
|
и
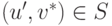
поскольку рулетка с компонентами
обеспечивает выполнение равенств
Далее, рулетка p* с компонентами
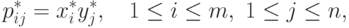 |
(
14.13)
|
также порождает допустимую точку
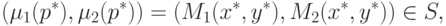 |
(
14.14)
|
которая, согласно (14.9), (14.12),
доминирует пару
(u*,v*). Заметим, что эта
последняя пара может и не быть допустимой.
Таким образом, в допустимом множестве S всегда есть вариант
сделки, превосходящий (возможно, нестрого) пару гарантированных уровней
( u*,v*), что и является основанием, определяющим интерес
сторон к кооперации. Следующий пример иллюстрирует отношения всех рассмотренных пар
выигрышей.
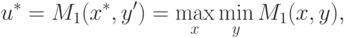
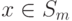 и
и 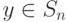 есть смешанные стратегии,
независимо используемые сторонами. Т.е. при оценке гарантированного
уровня мы исходим из того, что сторона P2 может вести себя как
противник стороны P1 в антагонистической игре
с матрицей A, характеризующей интересы P1. При
таком поведении стороны P2 ее ожидаемый выигрыш есть величина
есть смешанные стратегии,
независимо используемые сторонами. Т.е. при оценке гарантированного
уровня мы исходим из того, что сторона P2 может вести себя как
противник стороны P1 в антагонистической игре
с матрицей A, характеризующей интересы P1. При
таком поведении стороны P2 ее ожидаемый выигрыш есть величина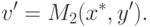
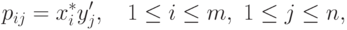
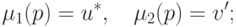
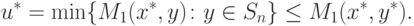

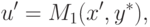
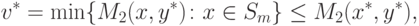
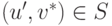 поскольку рулетка с компонентами
поскольку рулетка с компонентами