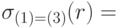Формализация реляционной модели

7.2. Манипулирование данными в реляционной модели

Для манипулирования данными в реляционной модели используются два формальных аппарата:

• реляционная алгебра, основанная на теории множеств;
• реляционное исчисление, базирующееся на исчислении предикатов первого порядка.

Механизмы реляционной алгебры и реляционного исчисления эквивалентны, т.е. для любого допустимого выражения реляционной алгебры можно построить эквивалентную формулу реляционного исчисления и наоборот.

Отличаются два этих формальных аппарата уровнем процедурности. Выражения реляционной алгебры строятся на основе алгебраических операций (высокого уровня), и подобно тому, как интерпретируются арифметические и логические выражения, выражение реляционной алгебры также имеет процедурную интерпретацию. Другими словами, запрос, представленный на языке реляционной алгебры, может быть реализован как последовательность элементарных алгебраических операций с учетом их старшинства и возможного наличия скобок.

Для формулы реляционного исчисления однозначная интерпретация (соответствующая однозначная последовательность действий), вообще говоря, отсутствует. Формула только устанавливает условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются более непроцедурными или декларативными.

Операции, реализуемые с помощью указанных аппаратов, обладают важным свойством: они замкнуты на множестве отношений. Это означает, что выражения реляционной алгебры и формулы реляционного исчисления определяются над отношениями реляционных БД и результатом вычисления также являются отношения. В результате любое выражение или формула могут интерпретироваться как отношение, что позволяет использовать их в других выражениях или формулах.

Как мы увидим, алгебра и исчисление обладают большой выразительной мощностью, очень сложные запросы к базе данных могут быть выражены с помощью одного выражения реляционной алгебры или одной формулы реляционного исчисления. Именно по этой причине такие механизмы включены в реляционную модель данных. Конкретный язык манипулирования реляционными БД называется реляционно полным, если любой запрос, выражаемый с помощью одной операции реляционной алгебры или одной формулы реляционного исчисления, может быть выражен с помощью одного оператора этого языка.

Заметим, что крайне редко алгебра или исчисление принимаются в качестве полной основы какого-либо языка БД. Обычно (как, например, в случае языка SQL) язык основывается на некоторой смеси алгебраических и логических конструкций. Тем не менее знание алгебраических и логических основ языков баз данных часто бывает полезно на практике.

7.3. Операции реляционной алгебры

Операции реляционной алгебры определены на множестве отношений и являются замкнутыми относительно этого множества (образуют алгебру). Оказывается, что любой произвольный запрос к БД можно представить в виде последовательности, составленной из пяти основных операций реляционной алгебры. Рассмотрим эти операции.

Объединение

Объединением отношений r и s называется множество кортежей, которые принадлежат или r, или s, или им обоим. Для операции объединения требуется одинаковая арность отношений.

Для примера, пусть

тогда

a	b	a
d	a	f
c	b	d
b	g	a

Заметим, что с помощью операции объединения может быть реализовано добавление нового кортежа к имеющемуся отношению. В этом случае r – исходное отношение, s – отношение, содержащее один добавляемый кортеж.

Разность r – s

Разностью отношений r и s называется множество кортежей, принадлежащих r, но не принадлежащих s. Для этой операции также требуется одинаковая арность отношений.

Заметим, что с помощью операции разности может быть реализовано удаление кортежа из имеющегося отношения. В этом случае r – исходное отношение, s – отношение, содержащее один удаляемый кортеж.

Декартово произведение r x s

Пусть r и s – отношения арности k1 и k2 соответственно. Декартовым произведением r x s называется множество кортежей длины k1+k2, первые k1 компонентов которых образуют кортежи, принадлежащие r, а последние k2 – кортежи, принадлежащие s.

Проекция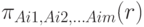

Проекция есть множество кортежей, получаемых из кортежей отношения r выбором столбцов с именами A_i1, A_i2, ..., A_im.

Другими словами, это операция построения "вертикального" подмножества, получаемого путем выбора определенных атрибутов и исключения остальных. Повторяющиеся кортежи исключаются.

a	a
d	f
c	d

Выбор ( селекция )

Пусть F – формула, образованная: операндами, являющимися константами или именами атрибутов, арифметическими операторами сравнения, логическими операторами (и, или, не), тогда выбором (селекцией) 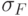называется множество кортежей, компоненты которого удовлетворяют условию, заданному формулой F.

a

b

a

Здесь F:(1)=(3) – содержимое первого столбца равно содержимому третьего столбца.

Приведем ряд примеров представления запросов с помощью формальных операций для реляционной модели (СТУДЕНТ, ФАКУЛЬТЕТ, СПЕЦИАЛЬНОСТЬ), рассмотренной выше.