Методы повышения экономической эффективности ПКС на основе моделирования и оптимизации внутрикорпоративных потоков

Управление рисками.Рассмотрим различные подходы к учету неопределенности при описании рисков. В теории принятия решений в настоящее время при компьютерном и математическом моделировании для описания неопределенностей чаще всего используют вероятностностатистические методы (прежде всего методы статистики нечисловых данных, в том числе интервальной статистики и интервальной математики). Полезны методы теории нечеткости и методы теории конфликтов (теории игр). Математический инструментарий применяется в имитационных, эконометрических, экономико-математических моделях, реализованных обычно в виде программных продуктов.

Некоторые виды неопределенностей связаны с безразличными к организации силами - природными (погодные условия) или общественными (смена правительства). Если явление достаточно часто повторяется, то его естественно описывать в вероятностных терминах. Так, прогноз урожайности зерновых вполне естественно вести в вероятностных терминах. Если же событие единично, то вероятностное описание вызывает внутренний протест, поскольку частотная интерпретация вероятности невозможна. Так, для описания неопределенности, связанной с исходами выборов или со сменой правительства, лучше использовать методы теории нечеткости и интервальной математики (интервал - удобный частный случай описания нечеткого множества). Наконец, если неопределенность связана с активными действиями соперников или партнеров, целесообразно применять методы анализа конфликтных ситуаций, т. е. методы теории игр, прежде всего антагонистических игр, но иногда полезны и более новые методы кооперативных игр, нацеленных на получение устойчивого компромисса.

Подходы к оцениванию рисков.Понятие "риск", как уже отмечалось, многогранно. Например, при использовании статистических методов управления качеством продукции риски (точнее, оценки рисков) - это вероятности некоторых событий. В статистическом приемочном контроле "риск поставщика" - это вероятность забракования партии продукции хорошего качества, а "риск потребителя" - приемки "плохой" партии. При статистическом регулировании технологических процессов рассматривают риск незамеченной разладки и риск излишней наладки.

Тогда оценка риска - это оценка вероятности, точечная или интервальная, по статистическим данным или экспертная. В таком случае для управления риском задают ограничения на вероятности нежелательных событий.

Иногда под уменьшением риска понимают уменьшение дисперсии случайной величины, поскольку при этом уменьшается неопределенность. В теории принятия решений риск - это плата за принятие решения, отличного от оптимального, он обычно выражается как математическое ожидание. В экономике плата измеряется обычно в денежных единицах, т. е. в виде финансового потока (потока платежей и поступлений) в условиях неопределенности.

Методы математического моделирования позволяют предложить и изучить разнообразные методы оценки риска. Широко применяются два вида методов - статистические, основанные на использовании эмпирических данных; экспертные, опирающиеся на мнения и интуицию специалистов.

Чтобы продемонстрировать сложность проблемы оценивания риска и различные существующие подходы, рассмотрим простейший случай. Пусть неопределенность носит вероятностный характер, а потери описываются одномерной случайной величиной (а не случайным вектором и не случайным процессом). Другими словами, ущерб адекватно описывается одним числом, а величина этого числа зависит от случая.

Итак, пусть величина порожденного риском ущерба моделируется случайной величиной Х (в смысле теории вероятностей). Как известно, случайная величина описывается функцией распределения

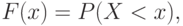
где 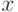- действительное число (т. е., как говорят и пишут математики, любой элемент действительной прямой, традиционно обозначаемой 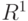). Поскольку 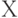обычно интерпретируется как величина ущерба, то 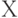- неотрицательная случайная величина.

В зависимости от предположений о свойствах функции распределения вероятностные модели риска делятся на параметрические и непараметрические. В первом случае предполагается, что функция распределения входит в одно из известных семейств распределений - нормальных (т. е. гауссовских), экспоненциальных или иных. Однако обычно подобное предположение является мало обоснованным - реальные данные не хотят "втискиваться" в заранее заданное семейство. Тогда необходимо применять непараметрические статистические методы, не предполагающие, что распределение ущерба взято из того или иного популярного среди математиков семейства. При использовании непараметрических статистических методов обычно принимают лишь, что функция распределения является непрерывной функцией числового аргумента .

Обсудим два распространенных заблуждения.

Во-первых, часто говорят, что поскольку величина ущерба зависит от многих причин, то она должна иметь т. н. нормальное распределение. Это неверно. Все зависит от способа взаимодействия причин. Если причины действуют аддитивно, то, действительно, в силу Центральной Предельной Теоремы теории вероятностей есть основания использовать нормальное (гауссово) распределение. Если же причины действуют мультипликативно, то в силу той же Центральной Предельной Теоремы теории вероятностей следует приближать распределение величины ущерба 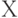с помощью логарифмически нормального распределения. Если же основное влияние оказывает " слабое звено" (где тонко, там и рвется), то согласно теоремам, доказанным академиком Б.В. Гнеденко, следует приближать распределение величины ущерба 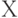с помощью распределения из семейства Вейбулла-Гнеденко. К сожалению, в конкретных практических случаях различить эти варианты обычно не удается.

Во-вторых, неверно традиционное представление о том, что реальные погрешности измерения нормально распределены. Проведенный многими специалистами тщательный анализ погрешностей реальных наблюдений показал, что их распределение в подавляющем большинстве случаев отличается от гауссова. Сводка этих исследований приведена в работе [ 16]. Среди специалистов распространено такое шуточное утверждение: " Прикладники обычно думают, что математики доказали, что погрешности распределены нормально, а математики считают, что прикладники установили это экспериментально".И те, и другие ошибаются. К сожалению, в настоящее время в экологической и экономической литературе имеется масса ошибочных утверждений. Существенная часть ошибок относится к использованию математических методов. Особенно это касается статистики и эконометрики. Причины появления ошибок разнообразны. Некоторые из них подробно обсуждаются в [ 13, 16].

Итак, рассмотрим ситуацию, когда возможная величина ущерба, связанного с риском, описывается функцией распределения 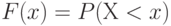.Обычно стараются перейти от функции, описываемой (с точки зрения математики) бесконечно большим числом параметров, к небольшому числу числовых параметров, лучше всего к одному. Для положительной случайной величины (величины ущерба) часто рассматривают такие ее характеристики, как

• математическое ожидание;
• медиана и, более общо, квантили, т. е. значения 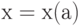, при которых функция распределения достигает определенного значения ; другими словами, значение квантили 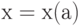находится из уравнения ;
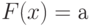• дисперсия (часто обозначаемая как - "сигмаквадрат");
• среднее квадратическое отклонение (квадратный корень из дисперсии, т. е. \sigma - "сигма");
• коэффициент вариации (среднее квадратическое отклонение, деленное на математическое ожидание);
• линейная комбинация математического ожидания и среднего квадратического отклонения (например, типично желание считать, что возможные значения ущерба расположены в таком интервале: математическое ожидание плюсминус три сигма );
• математическое ожидание функции потерь, и т. д. Этот перечень, очевидно, может быть продолжен.

Тогда задача оценки ущерба может пониматься как задача оценки той или иной из перечисленных характеристик. Чаще всего оценку проводят по эмпирическим данным (по выборке величин ущербов, соответствующим происшедшим ранее аналогичным случаям). При отсутствии эмпирического материала остается опираться на экспертные оценки,которым посвящена значительная часть следующей лекции. Наиболее обоснованным является модельнорасчетный метод,опирающийся на модели управленческой, экономической, социальнопсихологической, экологоэкономической ситуации, позволяющие рассчитать характеристики ущерба.

Характеристик случайного ущерба имеется много. Выше перечислено 7 видов; некоторые из них - второй, шестой и седьмой - содержат бесконечно много конкретных характеристик. Нельзя ограничиваться только средним ущербом, под которым обычно понимают математическое ожидание, хотя медиана ущерба не меньше соответствует этому термину. Весьма важны верхние границы для ущерба, т. е. квантили порядка , где близко к 1, например, . 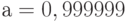При этом с вероятностью, не превосходящей 0,000001, реальный ущерб будет меньше 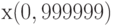. Сложные проблемы состоят в обоснованном вычислении границы 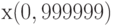, их мы не будем здесь касаться.

Что это такое - минимизация риска?Из предыдущих рассуждений следует, что минимизация риска может состоять:

1. в минимизации математического ожидания (ожидаемых потерь);
2. в минимизации квантиля распределения (например, медианы функции распределения потерь или квантиля порядка 0,99, выше которого располагаются большие потери, встречающиеся крайне редко - в 1 случае из 100);
3. в минимизации дисперсии (т. е. показателя разброса возможных значений потерь);
4. в минимизации суммы математического ожидания и утроенного среднего квадратического отклонения (на основе известного "правила трех сигм"), или иной линейной комбинации математического ожидания и среднего квадратического отклонения. Этот подход используют в случае близости распределения потерь к нормальному как комбинацию подходов, нацеленных на минимизацию средних потерь и разброса возможных значений потерь;
5. в максимизации математического ожидания функции полезности (в случае, когда полезность денежной единицы меняется в зависимости от общей располагаемой суммы, как предполагается в микроэкономике [ 20], когда необходимо исключить возможность разорения экономического агента), и т. д.

Перечень может быть продолжен. Например, не использована такая характеристика случайного ущерба, как коэффициент вариации. Однако целью изложения не является построение всеобъемлющей системы постановок задач минимизации риска, поэтому ограничимся сказанным.

Обсудим пять перечисленных постановок. Первая из них - минимизация средних потерь - представляется вполне естественной, если все возможные потери малы по сравнению с ресурсами предприятия. В противном случае первый подход неразумен. Рассмотрим условный пример. У человека имеется 10000 руб. Ему предлагается подбросить монету. Если выпадает "орел", то он получает 50000 руб. Если же выпадает "цифра", он должен уплатить 20000 руб. Стоит ли данному человеку участвовать в описанном пари? Если подсчитать математическое ожидание дохода, то поскольку каждая сторона монеты имеет одну и ту же вероятность выпасть, равную 0,5, оно равно 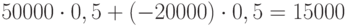. Казалось бы, пари весьма выгодно. Однако большинство людей на него не пойдет, поскольку с вероятностью 0,5 они лишатся всего своего достояния и останутся должны 10000 руб., т. е. разорятся. Здесь проявляется психологическая оценка ценности рубля, зависящая от общей имеющейся суммы - 10000 руб. для человека с обычным доходом значит гораздо больше, чем те же 10000 руб. для миллиардера.

Второй подход нацелен как раз на минимизацию больших потерь, на защиту от разорения. Другое его применение - исключение катастрофических аварий, например, типа чернобыльской. При втором подходе средние потери могут увеличиться (по сравнению с первым), зато максимальные будут контролироваться.

Третий подход нацелен на минимизацию разброса окончательных результатов. Средние потери при этом могут быть выше, чем при первом, но того, кто принимает решение, это не волнует - ему нужна максимальная определенность будущего, пусть даже ценой повышенных затрат.

Четвертый подход сочетает в себе первый и третий, хотя и довольно примитивным образом. Проблема ведь в том, что задача управления риском в рассматриваемом случае - это по крайней мере двухкритериальная задача. Желательно средние потери снизить (другими словами, математическое ожидание доходов повысить), и одновременно уменьшить показатель неопределенности - дисперсию. Хорошо известны проблемы, возникающие при многокритериальной оптимизации [ 17].

Наиболее продвинутый подход - пятый. Но для его применения необходимо построить функцию полезности. Это - большая самостоятельная задача. Обычно ее решают с помощью специально организованного эконометрического исследования.

Если неопределенность носит интервальный характер, т. е. описывается интервалами, то естественно применить методы статистики интервальных данных (как части интервальной математики), рассчитать минимальный и максимальный возможный доходы и потери, и т. д.

Разработаны различные способы уменьшения экономических рисков, связанные с выбором стратегий поведения, в частности, диверсификацией, страхованием и др. Причем эти подходы относятся не только к отдельным организациям. Применительно к системам налогообложения диверсификация означает использование не одного, а системы налогов, чтобы нейтрализовать действия налогоплательщиков, нацеленные на уменьшение своих налоговых платежей. Однако динамика реальных экономических систем такова, что любые формальные модели дают в лучшем случае только качественную картину. Например, не существует математических моделей, позволяющих достаточно точно спрогнозировать инфляцию вообще и даже реакцию экономики на одноразовое решение типа либерализации цен.

Необходимость применения экспертных оценок при оценке и управлении рисками.Из сказанного выше вытекает, что разнообразные формальные методы оценки рисков и управления ими во многих случаях (реально во всех нетривиальных ситуациях) не могут дать однозначных рекомендаций. В конце процесса принятия решения - всегда человек, менеджер, на котором лежит ответственность за принятое решение. Поэтому процедуры экспертного оценивания естественно применять на всех этапах анализа рисков рассматриваемого организацией проекта. При этом нецелесообразно полностью отказываться от использования формальноэкономических методов, например, основанных на вычислении чистых текущих потерь и других характеристик. Использование соответствующих программных продуктов полезно для принятия обоснованных решений. Однако на основные вопросы типа: достаточно ли высоки доходы, чтобы оправдать риск; или: что лучше - быстро, но мало, или долго, но много - ответить могут только менеджеры с помощью экспертов. Поэтому система поддержки принятия решений в организации должна сочетать формальноэкономические и экспертные процедуры.

Разработка системы поддержки принятия решений, нацеленной на оценивание рисков и управление ими, - непростое дело. Укажем несколько проблем, связанных с подобной работой. Совершенно ясно, что система должна быть насыщена конкретными численными данными об экономическом состоянии региона, страны, возможно и мира в целом. Добыть такие данные нелегко. Сводки Российского статистического агентства (ранее - Госкомстата РФ) искажены (подробнее о состоянии теории и практики статистики в России см. [ 13, 16]. В частности, Институт высоких статистических технологий и эконометрики МГТУ им. Н.Э. Баумана занялся изучением инфляции. Наши данные по этому показателю превышали данные Госкомстата РФ примерно в 2 раза (см. [ 16]). Зарубежные источники также содержат неточности. Так, при составлении балансовых соотношений для макроэкономических показателей по данным [8] выяснил ось, что государство должно иметь дополнительный источник доходов в несколько сотен миллиардов долларов, а доходы бизнеса имеют излишек в 30 млрд долл. Другими словами, популярное учебное пособие [ 8] содержит данные, не согласующиеся друг с другом.

Подходы к управлению рисками.При оценке, анализе и управлении рисками могут оказаться полезными известные публикации по методам учета финансового риска [ 1, 5, 19, 30, 32]. При использовании широкого арсенала статистических методов необходимо учитывать особенности их развития в России и СССР, наложившие свой отпечаток на современное состояние в области кадров и литературных источников.

Чтобы управлять, надо знать цель управления и иметь возможность влиять на те характеристики риска, которые определяют степень достижения цели.

Обычно можно выделить множество допустимых управляющих воздействий, описываемое с помощью соответствующего множества параметров управления. Тогда указанная выше возможность влиять на те характеристики риска, которые определяют степень достижения цели, формализуется как выбор значения управляющего параметра. Управляющий параметр может быть числом, вектором, быть элементом конечного множества или иметь более сложную математическую природу.

Основная проблема - корректная формулировка цели управления рисками. Поскольку существует целый спектр различных характеристик риска (например, если потери от риска моделируются случайной величиной), то оптимизация управления риском сводится к решению задачи многокритериальной оптимизации. Например, естественной является задача одновременной минимизации среднего ущерба (математического ожидания ущерба) и разброса ущерба (дисперсии ущерба).

Страхование и диверсификация - распространенные методы уменьшения неопределенности, присущей рискам, за счет повышения среднего уровня затрат. Выплата страховых взносов повышает затраты, но уменьшает неопределенность будущего. Если страховая компания полностью возмещает ущерб при осуществлении страхового случая, то неопределенность будущего полностью исчезает. При диверсификации хозяйственной деятельности упущенная выгода возникает из-за того, что средства вкладываются не только в самый выгодный (и самый рисковый) проект, но и в другие проекты. Если же нежелательные возможности осуществляются, "самый выгодный" проект приносит убытки, то другие проекты позволяют организации "остаться на плаву".

Как известно, для любой многокритериальной задачи целесообразно рассмотреть множество решений (т. е. значений параметра управления), оптимальных по Парето. Эти решения оптимальны в том смысле, что не существует возможных решений, превосходящих Паретооптимальные решения одновременно по всем критериям. Точнее, превосходили бы хотя бы по одному критерию, а по остальным были бы столь же хорошими. Теория Паретооптимальных решений хорошо развита [ 20].

Ясно, что для практической реализации надо выбирать одно из Паретооптимальных решений. Как выбирать? Разработан целый спектр подходов, из которых выбор может быть сделан только субъективным образом. Таким образом, снова возникает необходимость применения методов экспертных оценок.

Эксперты могут выбирать непосредственно из множества Паретооптимальных решений, если оно состоит лишь из нескольких элементов. Или же они могут выбирать ту или иную процедуру сведения многокритериальной задачи к однокритериальной. Один из подходов - выбрать т. н. "главный критерий", по которому проводить оптимизацию, превратив остальные критерии в ограничения. Например, минимизировать средний ущерб, потребовав, чтобы дисперсия ущерба не превосходила заданной величины.

Иногда задача многокритериальной оптимизации допускает декомпозицию. Найдя оптимальное значение для главного критерия, можно рассмотреть область возможных значений для остальных критериев, выбрать из них второй по важности и оптимизировать по нему, и т. д.

Что же делают эксперты? Они выбирают главный критерий (или упорядочивают критерии по степени важности), задают численные значения ограничений, иногда точность или время вычислений.

Второй основной подход - это свертка многих критериев в один интегральный и переход к оптимизации по одному критерию. Например, рассматривают линейную комбинацию критериев. Строго говоря, метод "главного критерия" - один из вариантов свертки. При этом вес главного критерия равен 1, а веса остальных - 0. Построение свертки, в частности, задание весов, целесообразно осуществлять экспертными методами.

Используют также методы, основанные на соображениях устойчивости (наиболее общий подход к изучению устойчивости разработан в [ 11]). При этом рассматривают область значений управляющих параметров, в которых значение оптимизируемого одномерного критерия (главного параметра или свертки) отличается от оптимального не более чем на некоторую заданную малую величину. Такая область может быть достаточно обширной. Например, если в линейном программировании (см., например, [ 15]) одна из граней многогранника, выделенного ограничениями, почти параллельна плоскости равных значений оптимизируемого критерия, то вся эта грань войдет в рассматриваемую область. В выделенной области можно провести оптимизацию другого параметра, и т. д. При таком подходе эксперты выбирают допустимое отклонение для основного критерия, выделяют второй критерий, задают ограничения и т. д.

Рассмотренные выше вероятностностатистические подходы к оцениванию рисков предполагают использование в качестве критериев таких характеристик случайной величины, как математическое ожидание, медиана, квантили, дисперсия и др. Эти характеристики определяются функцией распределения случайного ущерба, соответствующего рассматриваемому риску. При практическом использовании этого подхода перечисленные характеристики оцениваются по статистическим данным. Они оцениваются по выборке, состоящей из наблюденных величин ущерба. При этом необходимо вычислять доверительные интервалы, содержащие оцениваемые теоретические характеристики с заданной доверительной вероятностью [ 16]. Критерий, на использовании которого основана оптимизация, всегда определен лишь с некоторой точностью, а именно, лишь с точностью до полудлины доверительного интервала. Таким образом, приходим к постановке, рассмотренной в предыдущем абзаце.

Необходимо обратить внимание на существенное изменение ситуации в области вычислительной оптимизации за последние 60 лет. Если в 1960-е гг. из-за маломощности тогдашних компьютеров большое значение имела разработка быстрых методов счета, то в настоящее время внимание переносится на постановки задач и интерпретацию результатов. Это объясняется не только наличием различных программных продуктов по оптимизации, но и тем, что почти любую практическую задачу оптимизации можно решить простейшими методами типа переборных (перебирая возможные значения управляющих параметров с маленьким шагом), либо методом случайного поиска, поскольку быстродействие современных компьютеров позволяет это сделать.

В рискменеджменте (т. е. управлении рисками) компании целесообразно выделить оперативное управление рисками и стратегическое управление рисками. Первый вид деятельности - постоянно проводящаяся работа, связанная с обеспечением качества продукции, плановым снижением экологических рисков [ 15], работой с покупателями, поставщиками, персоналом, связанная с повышением лояльности, и т. д.

Стратегический рискменеджмент - составная часть стратегического планирования и управления. Надо оценивать риски высокого уровня, например, прогнозировать наличие в продаже, спрос и цену тех или иных товаров через 10-20 лет, например, нефти и "больших" компьютеров. Большое значение на этом уровне исследований имеют теория прогнозирования и экспертные оценки.