|
Здравствуйте,при покупке печатной формы сертификата,будут ли выданы обе печатные сторны? |
Лекция 7: Формальные спецификации, доказательство и верификация программ
6.1.3. Спецификации задач концепторным языком
Для постановки сложных математических задач (суммирование бесконечных рядов, теоретикомножественных операций с бесконечными множествами, гильбертов оператор и др.) и задач искусственного интеллекта (игры, распознавание образов и др.) предложен общематематический процедурный язык, так называемый концепторный язык - КЯ [6.17]. В этом языке процесс описания сложной задачи проводится путем обоснования решения задачи с математической точки зрения, затем формального описания постановок задач и, наконец, делается переход к алгоритмическому описанию.
Средства спецификации сложных задач.Основу КЯ составляет теоретикомножественный язык, который содержит декларативные и императивные средства теории множеств ЦермелоФренкеля. Ядро содержит набор элементов (типы, выражения, операторы) и средства определения новых типов, выражений и операторов.
Декларативные средства КЯ - это типизированный, многосортный логикоматематический язык задания выражений и структуризации множества значений (денотат). Выражения состоят из термов и формул, термы обозначают объекты ПрО, а формулы - утверждения об объектах и отношениях между ними. К конструкторам составных типов и формул относятся функторы, предикаты, конекторы и субнекторы.
Функтор - это конструктор, преобразующий термы в термы. Предикаты превращают термы в формулы, конекторы включают в себя логические связки и кванторы для преобразования одной формулы в другую. Субнектор (дескриптор) - это конструктор построения термов из выражений и формул. Конструкторы термов - это традиционные арифметические и алгебраические операции над числовыми множествами и вещественными функциями. Конструкторы формул включают в себя предикаты, состоящие из предикатных и числовых символов, а также конекторы, состоящие из логических связок, кванторов и конструкторов теории множеств.
Императивные средства КЯ - это операторы и процедуры для описания объектов ПрО с помощью концепторов, состоящих из разделов для определения объектов решаемой задачи и действий над ними. Каждый концептор - это именованный набор определений и действий со следующей структурой описания:
концептор К (< список параметров >) <список импортных параметров> <определение констант, типов, предикатов> <описание глобальных переменных> <определение процедур> начало К <тело концептора> конец К.
Концептор - это декларативное описание объектов и императивное описание операторов вычисления выражений тела. Рассматривается два случая:
- декларативный концептор состоит из определений параметров и типов;
- императивный концептор - это тело из операторов задач.
Декларативный концептор задает описание объектов и понятий, связанных с математической постановкой задачи, а описание метода ее решения с помощью императивных концепторов. Концепторное описание - это формальная спецификация задачи, которую можно трансформировать до алгоритмического описания и верификации.
Если полученный концептор неэффективен, то для повышения эффективности строится алгоритм, эквивалентный данному концептору. Он строится аппроксимацией концепторного решения путем замены неконструктивных объектов и неэффективных операций конструктивными и более эффективными аналогами.
Формализация КЯ. Общая схема формализации декларативной и императивной частей КЯ расширяется логикоматематическим языком, традиционными структурными операторами (присваивание, последовательность, цикл и т.п.), а также теоретикомодельными (денотационными) и аксиоматическими средствами формализации неконструктивной семантики КЯ.
Денотационный подход состоит в определении семантики языка путем подстановки каждому выражению соответствующего
элемента из множества денотатов функции  интерпретации символов сигнатуры языка.
Каждой константе
интерпретации символов сигнатуры языка.
Каждой константе 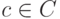 , функциональному символу
, функциональному символу  и предикатному символу
и предикатному символу 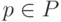 сопоставляется объект из множества денотат.
Этот способ интерпретации семантики выражений и операторов языка аналогичен денотационной семантики ЯП.
Главное отличие семантики КЯ от семантики программ - это ее неконструктивность.
С каждым КЯ можно связать некоторую дедуктивную теорию, которая отражает свойства концепторов.
сопоставляется объект из множества денотат.
Этот способ интерпретации семантики выражений и операторов языка аналогичен денотационной семантики ЯП.
Главное отличие семантики КЯ от семантики программ - это ее неконструктивность.
С каждым КЯ можно связать некоторую дедуктивную теорию, которая отражает свойства концепторов.
Формальная дедуктивная теория строится путем выделения из множества всех формул подмножества аксиом и правил вывода.
Для каждой пары 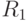 ,
, 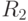 формул дедуктивной теории и каждого оператора
формул дедуктивной теории и каждого оператора 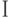 создается операторная формула
создается операторная формула  с утверждением,
что если
с утверждением,
что если 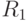 истинно перед выполнением оператора
истинно перед выполнением оператора  , то завершение оператора
, то завершение оператора  обеспечивает истинность
обеспечивает истинность 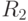 ,
т.е. формула
,
т.е. формула 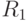 - предусловие, а
- предусловие, а 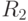 - постусловие оператора
- постусловие оператора  .
С помощью неконструктивных объектов и неразрешимых формул этой теории можно адекватно описывать свойства неэффективных процедур.
.
С помощью неконструктивных объектов и неразрешимых формул этой теории можно адекватно описывать свойства неэффективных процедур.
Аксиоматическое описание КЯ - это аксиомы и утверждения относительно концепторного описания и проведения дедуктивного доказательства и верификации этого описания.
Логико-алгебраические спецификации.При использовании этих спецификаций ПрО представляется в виде алгебраической системы с помощью соответствующих носителей, сигнатуры и трех принципов. Первый принцип - логико-алгебраическая спецификация ПрО и уточнение понятий ПрО, второй принцип - описание свойств ПрО в виде аксиом, которые формулируются в языке предикатов первого порядка и хорновских атомарных формул, и, наконец, третий принцип - это определение термальных моделей из основных термов спецификации. Логико-алгебраические спецификации можно ограничить хорновскими формулами из-за простоты аксиом и для упрощения процесса автоматического доказательства теорем. Отношения в сигнатурах спецификаций заменяются булевыми функциями.
Техника доказательного проектирования. Средства концепторной спецификации сложных, алгоритмически не разрешимых задач положены в основу формализованного описания поведения дискретных систем. Для описания свойств аппаратнопрограммных средств динамических систем применяются логико-алгебраические спецификации КЯ, техника описания которых включает два этапа.
На первом этапе дискретная система  рассматривается как черный ящик с конечным набором входов, выходов и состояний. Области значений входов и выходов - произвольные, а функционирование системы S - это набор частичных отображений и операций алгебраической системы. Они образуют частичную алгебру,формальное описание которой выполняется с помощью алгебраических спецификаций и является программой моделирования состояний дискретной системы.
рассматривается как черный ящик с конечным набором входов, выходов и состояний. Области значений входов и выходов - произвольные, а функционирование системы S - это набор частичных отображений и операций алгебраической системы. Они образуют частичную алгебру,формальное описание которой выполняется с помощью алгебраических спецификаций и является программой моделирования состояний дискретной системы.
На втором этапе система  детализируется в виде совокупности взаимозависимых подсистем
детализируется в виде совокупности взаимозависимых подсистем  , каждая из которой описывается алгебраической спецификацией.
В результате получается спецификация системы
, каждая из которой описывается алгебраической спецификацией.
В результате получается спецификация системы  из функций переходов и выходов, для которых необходимо доказывать корректность. Процесс детализации выполняется на уровне элементной базы или элементарных программ и сопровождается доказательством их корректности. В конечном итоге получается система S, эквивалентная исходной спецификации.
Примеры доказательства систем приведены в [6.17]. Рассмотрим один из них.
из функций переходов и выходов, для которых необходимо доказывать корректность. Процесс детализации выполняется на уровне элементной базы или элементарных программ и сопровождается доказательством их корректности. В конечном итоге получается система S, эквивалентная исходной спецификации.
Примеры доказательства систем приведены в [6.17]. Рассмотрим один из них.
Пусть требуется построить спецификацию натуральных чисел из множества этих чисел с сигнатурой операций  .
При построении используется число
.
При построении используется число  и функция следования
и функция следования 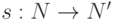 . Спецификация состоит из следующих аксиом:
. Спецификация состоит из следующих аксиом:
-
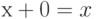 ,
, -
 ,
, -
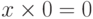 ,
, -
 ,
, -
 ,
, 
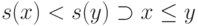
При этом алгебраические системы становятся многоосновными алгебрами, а аксиомы - спецификациями: тождественными и квазитождественными. Алгебраические спецификации - наиболее используемые, поскольку для них существуют эффективные алгоритмы выполнения, которые преобразуют спецификации в ЯП высокого уровня. Поэтому такие языки называют языками выполняемых логико-алгебраических спецификаций. Их операционная семантика основана на переписывании термов, а создаваемая алгебраическая спецификация получает логическую семантику, используемую при доказательстве теорем.
6.2. Методы доказательства правильности программ
Формальные методы тесно связаны с математическими техниками спецификаций, верификацией и доказательством правильности программ. Эти методы содержат математическую символику, формальную нотацию и аппарат вывода. Правила доказательства являются громоздкими и поэтому на практике редко используются рядовыми программистами. Однако с теоретической точки зрения они развивают логику применения математического метода индукции при проверке правильности программ. На основе спецификации программ проводится частичное и полное доказательство правильности программ [6.4, 6.5].
Под доказательством частичной правильности понимается проверка выполнения свойств данных программы с помощью утверждений, которые описывают то, что должна получить эта программа, когда закончится ее выполнение в соответствии с условиями заключительного утверждения. Полностью правильной программой по отношению к ее описанию и заданным утверждениям будет программа, если она частично правильная и заканчивается ее выполнение при всех данных, удовлетворяющих ей.
Для доказательства частичной правильности используется метод индуктивных утверждений, сущность которого состоит в следующем.
Пусть утверждение  связано с началом программы,
связано с началом программы,  - с конечной точкой программы и утверждение
- с конечной точкой программы и утверждение  отражает некоторые закономерности значений переменных,
по крайней мере, в одной из точек каждого замкнутого пути в программе (например, в циклах).
Если при выполнении программа попадает в
отражает некоторые закономерности значений переменных,
по крайней мере, в одной из точек каждого замкнутого пути в программе (например, в циклах).
Если при выполнении программа попадает в  -ю точку и справедливо утверждение
-ю точку и справедливо утверждение 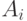 ,
а затем она проходит от точки
,
а затем она проходит от точки  к точке
к точке  , то будет справедливо утверждение
, то будет справедливо утверждение 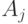 .
.
Теорема 6.1.
Если выполнены все действия метода индуктивных утверждений для программы, то она частично правильна относительно утверждений  ,
,  ,
,  .
.
Требуется доказать что, если выполнение программы закончится, то утверждение  будет справедливым.
По индукции, при прохождении точек программы, в которых утверждение
будет справедливым.
По индукции, при прохождении точек программы, в которых утверждение  будет справедливым,
то и
будет справедливым,
то и  -я точка программы будет такой же.
Таким образом, если программа прошла
-я точка программы будет такой же.
Таким образом, если программа прошла  -точку и утверждения
-точку и утверждения  и
и  справедливы,
то тогда, попадая из
справедливы,
то тогда, попадая из  -ой точки в
-ой точки в  точку, утверждение
точку, утверждение 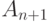 будет справедливым,
что и требовалось доказать.
будет справедливым,
что и требовалось доказать.
6.2.1. Характеристика формальных методов доказательства
Наиболее известными формальными методами доказательства программ являются метод рекурсивной индукции или утверждений Флойда, Наура, метод структурной индукции Хоара и др. [6.4, 6.5, 6.18, 6.19].
Метод Флойда основан на определении условий для входных и выходных данных и в выборе контрольных точек в доказываемой программе так, чтобы путь прохождения по программе пересекал хотя бы одну контрольную точку. Для этих точек формулируются утверждения о состоянии и значениях переменных в них (для циклов эти утверждения должны быть истинными при каждом прохождении циклаинварианта).
Каждая точка рассматривается для индуктивного утверждения того, что формула остается истинной при возвращении в эту точку программы и зависит не только от входных и выходных данных, но и от значений промежуточных переменных. На основе индуктивных утверждений и условий на аргументы создаются утверждения с условиями проверки правильности программы в отдельных ее точках. Для каждого пути программы между двумя точками устанавливается проверка на соответствие условий правильности и определяется истинность этих условий при успешном завершении программы на данных, удовлетворяющих входным условиям.
Формирование таких утверждений - довольно сложная задача, особенно для программ с высокой степенью параллельности и взаимодействия с пользователем. Кроме того, трудно проверить достаточность и правильность самих утверждений.
Доказательство корректности применялось для уже написанных программ и тех, которые разрабатываются методом последовательной декомпозиции задачи на подзадачи, для каждой из них формулируются утверждения с учетом условий ввода и вывода и точек программы, расположенными между входными и выходными утверждениями. Суть доказательства истинности выполнения условий и утверждений относительно заданной программы и составляет основу доказательства ее правильности.
Данный метод доказательства уменьшает число ошибок и время тестирования программы, обеспечивает отработку спецификаций программы на полноту, однозначность и непротиворечивость.
Метод Хоара - это усовершенствованный метод Флойда, основанный на аксиоматическом описании семантики языка программирования исходных программ. Каждая аксиома описывает изменение значений переменных с помощью операторов этого языка. Формализация операторов перехода и вызовов процедур обеспечивается с помощью правил вывода, содержащих индуктивные высказывания для каждой точки и функции исходной программы.
Система правил вывода дополняется механизмом переименования глобальных переменных, условиями на аргументы и результаты, а также на правильность задания данных программы. Оператор перехода трактуется как выход из циклов и аварийных ситуаций.
Описание с помощью системы правил утверждений - громоздкое и отличается неполнотой, поскольку все правила предусмотреть невозможно. Данный метод проверялся экспериментально на множестве программ без применения средств автоматизации из-за их отсутствия.
Метод Маккарти состоит в структурной проверке функций, работающих над структурными типами данных, структур данных и диаграмм перехода во время символьного выполнения программ. Эта техника включает в себя моделирование выполнения кода с использованием символов для изменяемых данных. Тестовая программа имеет входное состояние, данные и условия ее выполнения.
Выполняемая программа рассматривается как серия изменений состояний. Самое последнее состояние программы считается выходным состоянием и если оно получено, то программа считается правильной. Данный метод обеспечивает высокое качество исходного кода.
Метод Дейкстры предлагает два подхода к доказательству правильности программ. Первый подход основан на модели вычислений, оперирующей с историями результатов вычислений программы, анализом путей прохождения и правил обработки большого объема информации. Второй подход базируется на формальном исследовании текста программы с помощью предикатов первого порядка. В процессе выполнения программа получает некоторое состояние, которое запоминается для дальнейших сравнений.
Основу метода составляет математическая индукция, абстрактное описание программы и ее вычисление. Математическая индукция применяется при прохождении циклов и рекурсивных процедур, а также необходимых и достаточных условий утверждений. Абстракция позволяет сформулировать некоторые количественные ограничения. При вычислении на основе инвариантных отношений проверяются на правильность границы вычислений и получаемые результаты.
Процесс формального доказательства правильности программ методом математической индукции зарекомендовал себя как система правил статической проверки
правильности программ за столом для обнаружения в них формальных ошибок.
С помощью этого метода можно доказать истинность некоторого предположения 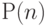 в зависимости
от параметра
в зависимости
от параметра  для всех
для всех  , и тем самым доказать случай
, и тем самым доказать случай 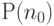 .
Исходя из истинности
.
Исходя из истинности 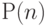 для любого значения
для любого значения  , доказывается
, доказывается 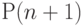 ,
что достаточно для доказательства истинности
,
что достаточно для доказательства истинности 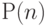 для всех
для всех  .
.
Путь доказательства следующий. Пусть даны описание некоторой правильной программы (ее логики) и
утверждение  относительно этой программы,
которая при выполнении достигает некоторой определенной точки.
Проходя через эту точку
относительно этой программы,
которая при выполнении достигает некоторой определенной точки.
Проходя через эту точку  раз, можно получить справедливость утверждения
раз, можно получить справедливость утверждения 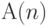 , если индуктивно доказать, что:
, если индуктивно доказать, что:
-
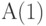 справедливо при первом проходе через заданную точку,
справедливо при первом проходе через заданную точку, - если
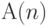 справедливо при
справедливо при  проходах через заданную точку,
то справедливо и
проходах через заданную точку,
то справедливо и 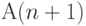 прохождение через заданную точку
прохождение через заданную точку  раз.
раз.
Исходя из предположения, что программа в конце концов успешно завершится, утверждение о ее правильности будет справедливым.

