|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Временная стоимость денег
Сама по себе сложная процентная ставка  ничем не отличается от простой и рассчитывается по такой же формуле (1). Сложная учетная ставка определяется по формуле (2). Так же как и в случае простых процентов возможно применение сложной учетной ставки для начисления процентов (антисипативный метод):
ничем не отличается от простой и рассчитывается по такой же формуле (1). Сложная учетная ставка определяется по формуле (2). Так же как и в случае простых процентов возможно применение сложной учетной ставки для начисления процентов (антисипативный метод):
 |
( 11) |
где 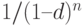 – множитель наращения сложных антисипативных процентов.
– множитель наращения сложных антисипативных процентов.
Однако практическое применение такого способа наращения процентов весьма ограничено и он относится скорее к разряду финансовой экзотики.
Как уже отмечалось, наиболее широко сложные проценты применяются при анализе долгосрочных финансовых операций 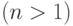 . На большом промежутке времени в полной мере проявляется эффект реинвестирования, начисления "процентов на проценты". В связи с этим вопрос измерения длительности операции и продолжительности года в днях в случае сложных процентов стоит менее остро. Как правило, неполное количество лет выражают дробным числом через количество месяцев (3/12 или 7/12), не вдаваясь в более точные подсчеты дней. Поэтому в формуле начисления сложных процентов число лет практически всегда обозначается буквой
. На большом промежутке времени в полной мере проявляется эффект реинвестирования, начисления "процентов на проценты". В связи с этим вопрос измерения длительности операции и продолжительности года в днях в случае сложных процентов стоит менее остро. Как правило, неполное количество лет выражают дробным числом через количество месяцев (3/12 или 7/12), не вдаваясь в более точные подсчеты дней. Поэтому в формуле начисления сложных процентов число лет практически всегда обозначается буквой  , а не выражением
, а не выражением 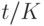 , как это принято для простых процентов. Наиболее щепетильные кредиторы, принимая во внимание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен целому числу лет: сложные проценты начисляются на период, измеренный
целыми годами, а проценты за дробную часть срока начисляются по простой процентной ставке.
, как это принято для простых процентов. Наиболее щепетильные кредиторы, принимая во внимание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен целому числу лет: сложные проценты начисляются на период, измеренный
целыми годами, а проценты за дробную часть срока начисляются по простой процентной ставке.
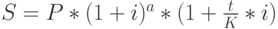 |
( 12) |
где  – число полных лет в составе продолжительности операции,
– число полных лет в составе продолжительности операции,
 – число дней в отрезке времени, приходящемся на неполный год,
– число дней в отрезке времени, приходящемся на неполный год,
 –временная база.
–временная база.
В этом случае вновь возникает необходимость выполнения календарных вычислений по рассмотренным выше правилам. Например, ссуда в 3 млн. рублей выдается 1 января 1997 года по 30 сентября 1999 года под 28% годовых (процентная ставка). В случае начисления сложных процентов за весь срок пользования деньгами наращенная сумма составит:

Если же использовать смешанный способ (например, коммерческие проценты с точным числом дней), то получим:

Таким образом, щепетильность кредитора в данном случае оказалась вовсе не излишней и была вознаграждена дополнительным доходом в сумме 85 тыс. рублей.
Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования начисленных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов. Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 1 тыс. рублей возрастет к концу года до 1,2 тыс. рублей (1 * (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 1,21 тыс. рублей (1 * (1 + 0,1) * (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 1,216 тыс. рублей. По мере увеличения числа начислений (  ) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном
наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой
) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном
наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой  . Формула наращения по сложным процентам при начислении их m раз в году имеет вид:
. Формула наращения по сложным процентам при начислении их m раз в году имеет вид:
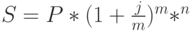 |
( 13) |
Например ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной процентной ставке 35% годовых с начислением процентов 2 раза в год. Будущая сумма к концу срока ссуды составит:
 .
.
При однократном начислении ее величина составила бы лишь 9,113 млн. рублей (5 * (1 + 0,35)^2; зато при ежемесячном начислении возвращать пришлось бы уже 9,968 млн. рублей (5 * 1 + (0,35 / 12)^(12 * 2)).
При начислении антисипативных сложных процентов, номинальная учетная ставка обозначается буквой  , а формула наращения принимает вид:
, а формула наращения принимает вид:
 |
( 14) |
Выражение 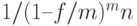 множитель наращения по номинальной учетной ставке.
множитель наращения по номинальной учетной ставке.
Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Последний менее выгоден для кредитора, чем учет по простой учетной ставке, поэтому используется крайне редко. В случае однократного начисления процентов его формула имеет вид:
 |
( 15) |
где 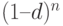 – дисконтный множитель банковского учета по сложной учетной ставке.
– дисконтный множитель банковского учета по сложной учетной ставке.
при  получаем
получаем
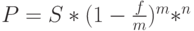 |
( 16) |
где  – номинальная сложная учетная ставка,
– номинальная сложная учетная ставка,
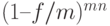 – дисконтный множитель банковского учета по сложной номинальной учетной ставке.
– дисконтный множитель банковского учета по сложной номинальной учетной ставке.
Значительно более широкое распространение имеет математическое дисконтирование по сложной процентной ставке  . Для
. Для 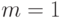 получаем
получаем
 |
( 17) |
где 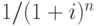 – дисконтный множитель математического дисконтирования по сложной процентной ставке.
– дисконтный множитель математического дисконтирования по сложной процентной ставке.
При неоднократном начислении процентов в течение года формула математического дисконтирования принимает вид:
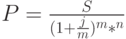 |
( 18) |
где  –номинальная сложная процентная ставка,
–номинальная сложная процентная ставка,
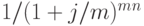 – дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.
– дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.
Например, требуется определить современную стоимость платежа в размере 3 млн. рублей, который должен поступить через 1,5 года, процентная ставка составляет 40%:
при 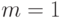
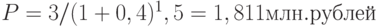
при  (начисление 1 раз в полугодие)
(начисление 1 раз в полугодие) 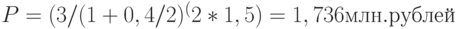
при  (ежемесячное начисление)
(ежемесячное начисление) 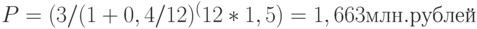 .
.
По мере увеличения числа начислений процентов в течение года (  ) промежуток времени между двумя смежными начислениями уменьшается – при
) промежуток времени между двумя смежными начислениями уменьшается – при  = 1 этот промежуток равен 1 году, а при
= 1 этот промежуток равен 1 году, а при  = 12 – только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бесконечнности, тогда величина промежутка между отдельными начислениями будет приближаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных аналитических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка (очевидно, что при непрерывном начислении речь может идти только о сложных процентах) обозначается буквой
= 12 – только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бесконечнности, тогда величина промежутка между отдельными начислениями будет приближаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных аналитических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка (очевидно, что при непрерывном начислении речь может идти только о сложных процентах) обозначается буквой 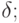 (читается "дельта"), часто этот показатель называют "сила роста". Формула наращения по непрерывной процентной ставке имеет вид:
(читается "дельта"), часто этот показатель называют "сила роста". Формула наращения по непрерывной процентной ставке имеет вид:
 |
( 19) |
где  – основание натурального логарифма (
– основание натурального логарифма ( 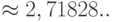 .),
.),
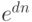 – множитель наращения непрерывных процентов.
– множитель наращения непрерывных процентов.
Например, чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня положить ее на банковский депозит под 15% годовых, начисляемых непрерывно?
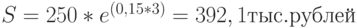 .
.
Для непрерывных процентов не существует различий между процентной и учетной ставками – сила роста является универсальным показателем. Однако, наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции). В этом случае можно строить очень мощные имитационные модели, однако математический аппарат расчета таких моделей достаточно сложен и не рассматривается в настоящем пособии, так же как и начисление процентов по переменной непрерывной процентной ставке.
Непрерывное дисконтирование с использованием постоянной силы роста выполняется по формуле:
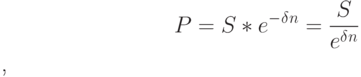 |
( 20) |
где  – дисконтный множитель дисконтирования по силе роста.
– дисконтный множитель дисконтирования по силе роста.
Например, в результате осуществления инвестиционного проекта планируется получить через 2 года доход в размере 15 млн. рублей. Чему будет равна приведенная стоимость этих денег в сегодняшних условиях, если сила роста составляет 22% годовых?
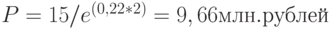 .
.

