Модели вычислений

Нетрадиционные архитектуры

Крутой подумал. Ему понравилось. Он решил когда-нибудь на досуге подумать еще раз. Русский анекдот

Исторический экскурс

Во время Великой французской революции в связи с введением метрической системы мер, да и для улучшения качества артиллерии и флота, возникла необходимость быстро и качественно пересчитать множество таблиц: артиллерийские, навигационные, астрономические, геодезические и т. п.

Решение этой задачи (вдохновителем и организатором работ был выдающийся математик и администратор Л. Карно) было гениально с точки зрения концептуальной и организационной проработки. Вначале с помощью методов интерполяции все функции были заменены их кусочно-полиномиальными приближениями, не имеющими разрывов (современный термин - сплайн). Полиномы могут вычисляться методом конечных разностей, поэтому алгоритм вычисления полинома был распределен на сложения, вычитания и небольшое число умножений на константы. Для организации таких вычислений было использовано две параллельно работающие роты грамотных солдат под руководством математиков. Одни и те же расчеты проводились ротами независимо. Каждый солдат получал аргументы от двух указанных ему товарищей, складывал либо вычитал их (действие было предопределено заранее и не менялось). Самые грамотные солдаты получали аргумент от одного товарища и умножали его на заданную константу. По команде результаты действий передавались далее. Математики-надзиратели проверяли полученные результаты на правдоподобие и пересчитывали их выборочно. В случаях расхождения результатов рот счет производился заново. Таким образом таблицы были пересчитаны практически без ошибок, с минимальными затратами, высокой точностью и в кратчайшее время. В результате артиллерийские таблицы французской армии оставались лучшими более пяти лет, до тех пор, пока русские артиллеристы под руководством гр. Аракчеева не посчитали их еще лучше ^{6Никто не знает, каким способом!}.

Так что в том первом историческом случае, когда значительный объем вычислений был индустриализирован, была весьма квалифицированно выбрана модель вычислений.

Именно этим примером руководствовался при создании первой программно-управляемой механической вычислительной машины Чарльз Бэббидж, поскольку на механических элементах невозможно было добиться приемлемой скорости без распараллеливания вычислений. Быстродействующие, но ненадежные элементы первых ЭВМ практически вынудили отказаться от параллельной модели вычислений и перейти к более примитивной последовательной модели. Все преподавание и математическое обеспечение стало развиваться с ориентацией на последовательные вычисления. И когда появилась возможность электронной реализации параллельных вычислений, к ней оказались не готовы ни математики, ни программисты.

Прежде всего, можно просто иметь несколько процессоров. Многопроцессорность может быть использована несколькими способами.

1. Можно увеличить надежность вычислений. В некоторых бортовых машинах, рассчитанных на длительную работу без обслуживания, три процессора считают каждую очередную команду. Тем самым сбой одного из них не страшен.
2. Можно вычислять одновременно несколько программ. В принципе, наибольшая производительность машины с несколькими процессорами достигается именно тогда, когда каждый из них работает со своей программой, расположенной в своей области памяти. В современных машинах по сути дела именно так совмещается работа центрального процессора и устройств управления вводом, выводом и отображением информации. Но переносу этого принципа на саму архитектуру машины мешает привычка к рассмотрению ее как устройства для выполнения непосредственно нужной в данный момент задачи.
3. В связи с этим имеется, насколько известно автору, ни разу не использованное решение (предложенное автором еще в начале 70-х гг., но тогда отвергнутое). Поскольку каналы связи с памятью являются неустранимым узким местом, можно было бы снабдить процессор несколькими каналами и одновременно выполнять на одном процессоре несколько независимых программ. Вследствие этого можно было бы обойтись маленьким кэшем, состоящим из действительно нужных команд и данных (следующих команд и данных каждого из процессов).
4. И, наконец, можно попытаться использовать несколько процессоров для одного и того же процесса над общей памятью. В этом случае нужны изощренные алгоритмы кэширования и распределения программ между процессорами, а производительность растет всего лишь пропорционально корню квадратному от числа процессоров (и то в лучшем случае!) Получается, как зачастую бывает в современной информатике, круто, но весьма нерационально.

   Прямое развитие данной идеи наталкивается также на массу тонких вопросов синхронизации. Простейший и наиболее очевидный из конфликтов синхронизации - попытка одновременной записи результатов нескольких команд в одну ячейку памяти, поэтому присваивания становятся тормозом на пути программирования.

Рассмотрим теперь те архитектуры, где до известной степени ликвидируется централизованное управление и появляется возможность глубокого распараллеливания вычислений.

Здесь стоит обратить внимание на два взаимосвязанных момента. Во-первых, часто нет нужды в хранении промежуточных результатов счета и, как следствие, потребность в пассивной памяти существенно снижается. Во-вторых, ликвидируется примитивное устройство управления, а его роль принимают на себя элементы оборудования, отвечающие за выяснение готовности команд к выполнению. Это - одна из схем, которая подчиняет управление потокам данных (data flow). Такие схемы противопоставляются управляющим потокам (control flow) традиционных вычислений.

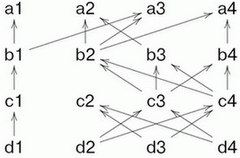
Рассмотрим гипотетическую схему машины, управляемой потоком данных. Каждая команда имеет ссылку на те команды, от которых она зависит ( предпосылки команды). Если выполнены все предпосылки, команда имеет право выполниться. Например, рассмотрим следующую схему.

Рис. 2.4. Поток данных

На схеме вершины означают команды. Каждая команда зависит не более чем от двух, но зависеть от нее может сколько угодно других.

Представленная идея неоднократно воплощалась в оборудовании (так называемые машины потоков данных). Но каждый раз узким местом для подобных машин оказывалось несоответствие стиля программ, требуемого для них, тем стилям, к которым привыкли программисты. Как следствие, в каждом из таких процессоров делались грубые системные ошибки, приводившие к затруднениям в программировании, а также к понижению скорости и гибкости вычислений. Тем не менее поскольку скорость света очень скоро поставит предел механическому увеличению пропускной способности каналов, к подобным схемам придется вернуться на другом уровне.

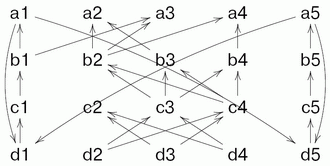
Конечно же, при реализации идеи возникают сложности. Пару из них демонстрирует следующий поток.

Рис. 2.5. Поток данных с взаимодействующими циклами

В потоке имеются два цикла, подготавливающие данные друг для друга. Возникает вопрос, а если один из циклов вторично подошел к точке, где требуются данные из другого, не устарели ли уже имеющиеся данные и не нужно ли подождать, пока они обновятся? Далее, здесь видно, что инициализацию потока данных часто необходимо выделять в самостоятельный блок, поскольку формально вычисление обоих циклов просто не сможет начаться.

Машины потоков данных уже несколько десятилетий используются на практике, так называемые суперЭВМ считают вычислительные задачи колоссальной трудоемкости (например, метеорологические). В подобных задачах, как правило, вычисление может быть записано в матричной алгебре, и новые матрицы строка за строкой вычисляются по старым. Таким образом, можно организовать конвейер, когда элементы целого вектора данных параллельно считаются по элементам предшествующего вектора, а переход к следующему происходит, когда все новые элементы посчитаны (так что вопрос о старении данных решается радикально: все, что использовалось для предыдущего вектора, по умолчанию считается устаревшим для следующего). Особенно хорошо конвейер работает, когда подпрограммы вычисления для каждого из элементов массива практически не изменяются (конечно же, для разных элементов они могут быть разные), поскольку инициализация процесса занимает много времени и сил. Конвейер с 1024 процессорами увеличивает производительность вычислений для некоторых реальных задач примерно в 300 раз, и для многих приблизительно в 100 раз. Первой серийной суперЭВМ, успешно применившей конвейерную организацию, стала система машин Cray.

Одной из особенностей машин потоков данных является повышение активности памяти, в которой размещаются команды и их операнды. По этому пути можно пойти еще дальше, сделав всю память активной. Во избежание полной анархии, память обычно имеет общее устройство управления, задающее одну команду (или несколько команд, в зависимости от какого-то быстро проверяемого условия), которую выполняют все ячейки ( ассоциативная память ). История реализации этой идеи аналогична истории машин потоков данных: аппаратные предпосылки есть, но эффективных способов программирования нет.

Несмотря на очевидные преимущества для отдельных классов задач других моделей вычислений и на очевидную неэффективность классической модели вычислений, не происходит переход к другим, более перспективным с точки зрения ускорения счета, моделям. Почему? Это очень непростой вопрос, связанный как со сложившимися традициями, так и с огромным грузом накопленного программного обеспечения. В частности, другие модели вычислений, очевидно, не универсальны, ориентированы на некоторые классы задач, а иллюзия универсальности, основанная на примитивно истолкованной теореме об универсальном алгоритме, сопутствует традиционной модели вычислений. Но, пожалуй, более всего консерватизм обусловлен тем, что сегодняшняя армия программистов воспитана на традиционной модели, и она уже не в состоянии перестроиться.

Уже в машине потоков данных мы видим, что приказ выполнить следующую команду может быть заменен на разрешение ее выполнить. Таким образом, в программировании имеется возможность перехода от повелительного наклонения к изъявительному. Реализация идеи внедрения изъявительного наклонения в языки программирования возможна по следующим направлениям:

• Системы продукций. Соотношения записываются как правила вывода предложения в некоторой грамматической или логической форме. Обрабатываемые данные сопоставляются с шаблонами, задаваемыми частями правил, отвечающими за распознавание ситуации, когда правило может быть применено. Соответствие данных шаблону трактуется как разрешение применить данное правило. Применение правила состоит в замене выделенного при сопоставлении фрагмента данных на что-то другое. Однократное выполнение такой замены трактуется как атомарный акт вычисления.
• Системы функций. Программа есть соотношение между функциями, связанными между собой аргументами, которые, в свою очередь, могут быть функциями. Таким образом, атомарный акт вычислений - это подготовка аргументов для использующей функции. Готовность аргументов трактуется как разрешение вычисления функции.
• Коммутационные системы. Элемент системы - вершина графа, имеющая входные и выходные места. Входные места служат концами дуг, а выходные, соответственно, их началами. Дуги - это каналы передачи значений. Вершины, в свою очередь, могут иметь внутреннюю графовую структуру, и так далее по рекурсии. Программа есть граф с двумя выделенными вершинами, одна из которых не имеет входных мест ( генератор перерабатываемых данных), а вторая не имеет выходных мест ( получатель результата). Элементарное вычисление на графе может активизироваться, когда ко всем входам вершины поступают значения, и в этом случае либо производятся предопределенные языком действия (когда вершина атомарна), либо значения передаются по внутренней структуре к вложенным вершинам. Результатом вычисления являются значения на выходных местах.

  Способ передачи данных и активизации вычислений в коммутационной системе может рассматриваться как одна из реализаций потока данных в системе функций. В частности, если граф не имеет циклов, то коммутационная система становится формой представления нерекурсивной системы функций. Если граф коммутационной системы содержит циклы, то он может быть интерпретирован как рекурсивная система функций. Такая система может быть теоретически представлена как бесконечный ациклический граф.
• Ассоциативные системы. Элементы системы - активные данные, представляющие собой пары: (значение, ключ) Пары, имеющие одинаковые ключи, соединяются и используются в качестве аргументов действия, закодированного ключом. Алгоритм действия может быть задан в любом стиле (например, в рамках традиционного программирования), его результатом для системы является набор пар, порождаемых в ходе локального действия, а исходные аргументы при этом уничтожаются. Легко заметить, что ассоциативная система может рассматриваться как иная форма коммутационной системы, и с точки зрения возможностей, предоставляемых для программирования, они теоретически эквивалентны. Однако эта форма соответствует иному взгляду на описываемые вычисления, который лучше подходит, в частности, для работы с базами знаний ^{7Теоретическая эквивалентность понятий означает для программиста выбор между двумя формами представления, которые практически неэквивалентны!}.
• Аксиоматические системы. Если система отождествлений и замен фиксирована для целых классов задач и предметных областей, то мы работаем в фиксированном классе исчислений, и на первый план выходит задача описания знаний и предпочтений на фиксированном языке. Знания и предпочтения записываются в виде аксиом. Таким образом, формально аксиоматические системы являются частным случаем сентенциальных, но фиксированные правила замен позволяют перейти от общего пошагового моделирования символьных преобразований к неизмеримо более эффективному выводу, когда планируется сразу целая система преобразований ^{8Говорить о цепочке преобразований здесь слишком скромно, поскольку в развитых аксиоматических системах вывод является сложной иерархической структурой, а алгоритмы поиска вывода сразу планируют эту структуру.}.

  В случае наиболее распространенной классической логики и языка исчисления предикатов либо некоторого его расширения на систему аксиом можно смотреть как на описание предметной области (либо, что то же самое, на задание соотношений между данными). Вычислительные действия в подобной системе активизируются по запросам, целью которых является вывод некоторой формулы (что для классической логики и элементарных формул соответствует выводу истинности либо ложности некоторого факта; такой вывод уже не назовешь проверкой, поскольку он не является элементарной операцией). Программиста в такой системе обычно интересует не способ вывода, а лишь его осуществимость.

Все описанное выше если и может быть сегодня реализовано в оборудовании, то крайне ущербным и частным способом. Но еще в 60-е гг. ХХ века стало видно, что программное обеспечение настолько сильно экранирует физическую структуру компьютера, что для всех пользователей и большинства программистов компьютер вместе с базовым программным обеспечением является единой системой. В связи с этим все чаще говорят о системе программирования как о машине. Например, реализация языка Java определяется через Java-машину, в терминах которой понимаются все вычисления. Достаточно часто такая программная машина, реализующая некоторую модель вычислений, служила основой для аппаратной реализации ключевых особенностей данной модели. Например, Алгол-машина легла в основу компьютеров со стековой архитектурой и тегированием.