|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Хэш-функции и аутентификация сообщений. Часть 2
Хэш-функции SHA-2
В 2001 году NIST принял в качестве стандарта три хэш-функции с существенно большей длиной хэш-кода. Часто эти хэш-функции называют SHA-2 или SHA-256, SHA-384 и SHA-512 (соответственно, в названии указывается длина создаваемого ими хэш-кода). Эти алгоритмы отличаются не только длиной создаваемого хэш-кода, но и длиной обрабатываемого блока, длиной слова и используемыми внутренними функциями. Сравним характеристики этих хэш-функций.
Под безопасностью здесь понимается стойкость к атакам типа "парадокса дня рождения".
В данных алгоритмах размер блока сообщения равен m бит. Для SHA-256 m = 512, для SHA-384 и SHA-512 m = 1024. Каждый алгоритм оперирует с w-битными словами. Для SHA-256 w = 32, для SHA-384 и SHA-512 w = 64. В алгоритмах используются обычные булевские операции над словами, а также сложение по модулю 2w, правый сдвиг на n бит SHRn (x), где х - w-битное слово, и циклические (ротационные) правый и левый сдвиги на n бит ROTRn (x) и ROTLn (x), где х - w-битное слово.
SHA-256 использует шесть логических функций, при этом каждая из них выполняется с 32-битными словами, обозначенными как x, y и z. Результатом каждой функции тоже является 32-битное слово.
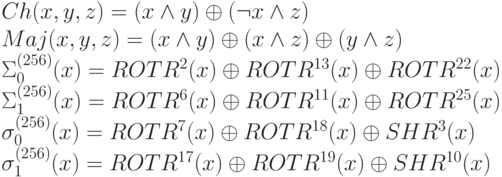
SHA-384 и SHA-512 также используют шесть логических функций, каждая из которых выполняется над 64-битными словами, обозначенными как x, y и z. Результатом каждой функции является 64-битное слово.
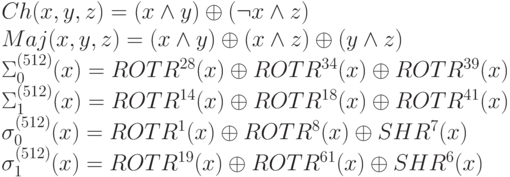
Предварительная подготовка сообщения, т.е. добавление определенных
битов до целого числа блоков и последующее разбиение на блоки
выполняется аналогично тому, как это делалось в SHA-1 (конечно, с
учетом длины блока каждой хэш-функции). После этого каждое сообщение
можно представить в виде последовательности N блоков M(1), M(2), 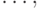 M(N).
M(N).
Рассмотрим SHA-256. В этом случае инициализируются восемь 32-битных переменных, которые послужат промежуточным значением хэш-кода:
a, b, c, d, e, f, g, h
Основой алгоритма является модуль, состоящий из 64 циклических обработок каждого блока M(i):
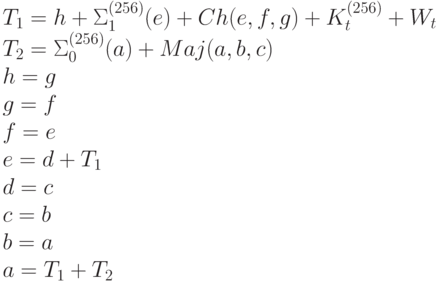
где Ki{256} - шестьдесят четыре 32-битных константы, каждая из которых является первыми 32-мя битами дробной части кубических корней первых 64 простых чисел.
Wt вычисляются из очередного блока сообщения по следующим правилам:
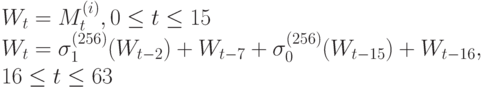
i-ое промежуточное значение хэш-кода H(t) вычисляется следующим образом:
H0(i) = a + H0(i-1) H1(i) = b + H1(i-1) H2(i) = c + H2(i-1) H3(i) = d + H3(i-1) H4(i) = e + H4(i-1) H5(i) = f + H5(i-1) H6(i) = g + H6(i-1) H7(i) = h + H7(i-1)
Теперь рассмотрим SHA-512. В данном случае инициализируются восемь 64-битных переменных, которые будут являться промежуточным значением хэш-кода:
a, b, c, d, e, f, g, h
Основой алгоритма является модуль, состоящий из 80 циклических обработок каждого блока M(i):
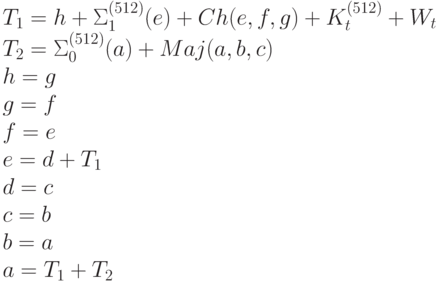
где Ki{512} - восемьдесят 64-битных констант, каждая из которых является первыми 64-мя битами дробной части кубических корней первых восьмидесяти простых чисел.
Wt вычисляются из очередного блока сообщения по следующим правилам:
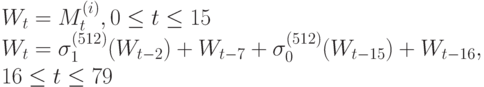
i-ое промежуточное значение хэш-кода H(t) вычисляется следующим образом:
H0(i) = a + H0(i-1) H1(i) = b + H1(i-1) H2(i) = c + H2(i-1) H3(i) = d + H3(i-1) H4(i) = e + H4(i-1) H5(i) = f + H5(i-1) H6(i) = g + H6(i-1) H7(i) = h + H7(i-1)
Рассмотрим SHA-384. Отличия этого алгоритма от SHA-512:
- Другой начальный хэш-код H(0).
- 384-битный дайджест получается из левых 384 битов окончательного хэш-кода H(N):
H0(N) || H1(N) || H2(N) || H3(N) || H4(N) || H5(N).
Хэш-функция ГОСТ 34.11
Алгоритм ГОСТ 34.11 является отечественным стандартом для хэш-функций. Его структура довольно сильно отличается от структуры алгоритмов SHA-1, 2 или MD5, в основе которых лежит алгоритм MD4.
Длина хэш-кода, создаваемого алгоритмом ГОСТ 34.11, равна 256 битам. Алгоритм разбивает сообщение на блоки, длина которых также равна 256 битам. Кроме того, параметром алгоритма является стартовый вектор хэширования Н - произвольное фиксированное значение длиной также 256 бит.
Алгоритм обработки одного блока сообщения
Сообщение обрабатывается блоками по 256 бит справа налево.
Каждый блок сообщения обрабатывается по следующему алгоритму.
- Генерация четырех ключей длиной 256 бит каждый.
- Шифрование 64-битных значений промежуточного хэш-кода H на ключах Ki(i = 1, 2, 3, 4) с использованием алгоритма ГОСТ 28147 в режиме простой замены.
- Перемешивание результата шифрования.
Для генерации ключей используются следующие данные:
- промежуточное значение хэш-кода Н длиной 256 бит;
- текущий обрабатываемый блок сообщения М длиной 256 бит;
- параметры - три значения С2, С3 и С4 длиной 256 бит следующего вида: С2 и С4 состоят из одних нулей, а С3 равно
18 08 116 024 116 08 (08 18)2 18 08 (08 18)4 (18 08)4
где степень обозначает количество повторений 0 или 1.
Используются две формулы, определяющие перестановку и сдвиг.
Перестановка Р битов определяется следующим образом: каждое 256-битное значение рассматривается как последовательность тридцати двух 8-битных значений.
Перестановка Р элементов 256-битной последовательности выполняется по
формуле 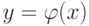 , где x - порядковый номер 8-битного значения в
исходной последовательности; y - порядковый номер 8-битного значения
в результирующей последовательности.
, где x - порядковый номер 8-битного значения в
исходной последовательности; y - порядковый номер 8-битного значения
в результирующей последовательности.

Сдвиг А определяется по формуле

Где
Присваиваются следующие начальные значения:
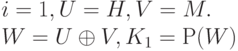
Ключи K2, K3, K4 вычисляются последовательно по следующему алгоритму:
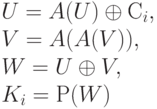
Далее выполняется шифрование 64-битных элементов текущего значения хэш-кода Н с ключами K1, K2, K3 и K4. При этом хэш-код Н рассматривается как последовательность 64-битных значений:
H = h4 || h3 || h2 || h1
Выполняется шифрование алгоритмом ГОСТ 28147:
si = EKi [hi] i = 1, 2, 3, 4 S = s1 || s2 || s3 || s4
Наконец на заключительном этапе обработки очередного блока
выполняется перемешивание полученной последовательности. 256-битное
значение рассматривается как последовательность шестнадцати 16-битных
значений. Сдвиг обозначается  и определяется следующим образом:
и определяется следующим образом:
Результирующее значение хэш-кода определяется следующим образом:
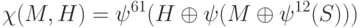
где
Логика выполнения ГОСТ 34.11
Входными параметрами алгоритма являются:
- исходное сообщение М произвольной длины;
- стартовый вектор хэширования Н, длина которого равна 256 битам;
-
контрольная сумма
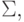 начальное значение которой равно нулю и длина
равна 256 битам;
начальное значение которой равно нулю и длина
равна 256 битам; - переменная L, начальное значение которой равно длине сообщения.
Сообщение М делится на блоки длиной 256 бит и обрабатывается справа налево. Очередной блок i обрабатывается следующим образом:
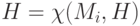
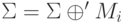
- L рассматривается как неотрицательное целое число, к этому числу прибавляется 256 и вычисляется остаток от деления получившегося числа на 2256. Результат присваивается L.
Где  обозначает следующую операцию:
обозначает следующую операцию:  и Mi рассматриваются как
неотрицательные целые числа длиной 256 бит. Выполняется обычное
сложение этих чисел и находится остаток от деления результата
сложения на 2256. Этот остаток и является результатом операции.
и Mi рассматриваются как
неотрицательные целые числа длиной 256 бит. Выполняется обычное
сложение этих чисел и находится остаток от деления результата
сложения на 2256. Этот остаток и является результатом операции.
Самый левый, т.е. самый последний блок М' обрабатывается следующим образом:
- Блок добавляется слева нулями так, чтобы его длина стала равна 256 битам.
- Вычисляется
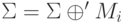 .
. - L рассматривается как неотрицательное целое число, к этому числу прибавляется длина исходного сообщения М и находится остаток от деления результата сложения на 2256.
- Вычисляется
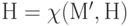 .
. - Вычисляется
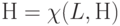 .
. - Вычисляется
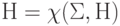 .
.
Значением функции хэширования является Н.


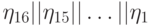 - исходное значение
- исходное значение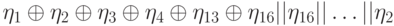 - результирующее
значение
- результирующее
значение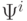 - i-ая степень преобразования
- i-ая степень преобразования