Моделирование процессов управления

О методологии моделирования

Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до теоретической чисто математической задачи. Второй - внутриматематическое изучение и решение этой задачи. Третий - переход от математических выводов обратно к практической проблеме.

В области моделирования процессов управления, как, впрочем, и в иных областях применения математики, целесообразно выделять четверки составляющих:

ЗАДАЧА - МОДЕЛЬ - МЕТОД - УСЛОВИЯ ПРИМЕНИМОСТИ.

Обсудим каждую из только что выделенных составляющих.

Задача, как правило, порождена потребностями той или иной прикладной области. Вполне понятно, что при этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у экономистов - маркетологов возникает вопрос: различаются ли мнения двух групп потребителей. При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин, а вопрос маркетологов переформулируется в рамках этой модели как вопрос о проверке той или иной статистической гипотезы однородности. Речь может идти об однородности характеристик, например, о проверке равенства математических ожиданий, или о полной (абсолютной однородности), т.е. о совпадении функций распределения, соответствующих двух совокупностям.

Задача может быть порождена также обобщением потребностей ряда прикладных областей. Приведенный выше пример иллюстрирует эту ситуацию: к необходимости проверки гипотезы однородности приходят и медики при сравнении двух групп пациентов, и инженеры при сопоставлении результатов обработки деталей двумя способами, и т.д. Таким образом, одна и та же математическая модель может применяться для решения самых разных по своей прикладной сущности задач.

Важно подчеркнуть, что выделение перечня задач находится вне математики. Выражаясь инженерным языком, этот перечень является сутью технического задания, которое специалисты различных областей деятельности дают специалистам по математическому моделированию.

Метод, используемый в рамках определенной математической модели - это уже во многом, если не в основном, дело математиков. В эконометрических моделях речь идет, например, о методе оценивания, о методе проверки гипотезы, о методе доказательства той или иной теоремы, и т.д. В первых двух случаях алгоритмы разрабатываются и исследуются математиками, но используются прикладниками, в то время как метод доказательства касается лишь самих математиков.

Ясно, что для решения той или иной задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. Приведем примеры. Для специалистов по теории вероятностей и математической статистике наиболее хорошо известна история Центральной Предельной Теоремы теории вероятностей. Предельный нормальный закон был получен многими разными методами, из которых напомним теорему Муавра-Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, завершающие эпопею методы, примененные Линдебергом и Феллером. В настоящее время для решения практически важных задач могут быть использованы современные информационные технологии на основе метода статистических испытаний и соответствующих датчиков псевдослучайных чисел. Они уже заметно потеснили асимптотические методы математической статистики. В рассмотренной выше проблеме однородности для проверки одной и той же гипотезы совпадения функций распределения могут быть применены самые разные методы - Смирнова, Лемана - Розенблатта, Ви лкоксона и др.

Наконец, рассмотрим последний элемент четверки - условия применимости. Он - полностью внутриматематический. С точки зрения математика замена условия (кусочной) дифференцируемости некоторой функции на условие ее непрерывности может представляться существенным научным достижением, в то время как прикладник оценить это достижение не сможет. Для него, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от (кусочно) дифференцируемых. Точнее, они одинаково хорошо (или одинаково плохо) могут быть использованы для описания реальной действительности.

Методологический анализ - первый этап моделирования процессов управления, да и вообще любого исследования. Он определяет исходные постановки для теоретической проработки, а потому во многом и успех всего исследования. Анализ динамики развития методов моделирования позволяет выделить наиболее перспективные методы. В частности, при вероятностно-статистическом моделировании наиболее перспективными оказались методы нечисловой статистики.

Модель управления обучением

В качестве примера конкретной модели процесса управления рассмотрим модель распределения времени между овладением знаниями и развитием умений

Любое знание состоит частично из "информации" ("чистое знание") и частично из "умения" ("знаю как"). Умение - это мастерство, это способность использовать имеющиеся у вас сведения для достижения своих целей; умение можно еще охарактеризовать как совокупность определенных навыков, в конечном счете, умение - это способность методически работать.

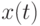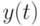Пусть - объем сведений, накопленных учащимся к моменту времени ("чистое знание"), - объем накопленных умений: умений рассуждать, решать задачи, разбираться в излагаемом преподавателем материале; - доля времени, отведенного на накопление знаний в промежутке времени .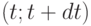

Естественно считать, что увеличение 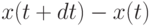объема знаний учащегося пропорционально потраченному на это времени и накопленным умениям 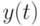. Следовательно,

( 1)

где коэффициент 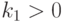зависит от индивидуальных особенностей учащегося.

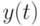Увеличение знаний за то же время пропорционально потраченному на это времени , имеющимся умениям и знаниям 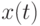. Следовательно,

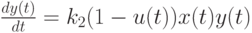( 2)

Коэффициент 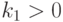также зависит от индивидуальности. Учащийся тем быстрее приобретает умения, чем больше он уже знает и умеет. Тем быстрее усваивает знания, чем больше умеет. Но нельзя считать, что чем больше они запомнил, тем быстрее запоминает. На правую часть уравнения (1) влияют только приобретенные в прошлом активные знания, примененные при решении задач и перешедшие в умения. Отметим, что модель (1) - (2) имеет смысл применять на таких интервалах времени, чтобы, например, пять минут можно было считать бесконечно малой величиной.

Можно управлять процессом обучения, выбирая при каждом значение функции из отрезка . Рассмотрим две задачи.

1. Как возможно быстрее достигнуть заданного уровня знаний и умений 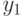? Другими словами, как за кратчайшее время перейти из точки фазовой плоскости 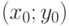в точку ?

2. Как быстрее достичь заданного объема знаний, т.е. выйти на прямую ?

Двойственная задача: за заданное время достигнуть как можно большего объема знаний. Оптимальные траектории движения для второй задачи и двойственной к ней совпадают (двойственность понимается в обычном для математического программирования смысле).

С помощью замены переменных 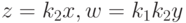перейдем от системы (1) - (2) к более простой системе дифференциальных уравнений, не содержащей неизвестных коэффициентов:

( 3)

(Описанная линейная замена переменных эквивалентна переходу к другим единицам измерения знаний и умений, своим для каждого учащегося.)

Решения задач 1 и 2, т.е. наилучший вид управления , находятся с помощью математических методов оптимального управления, а именно, с помощью принципа максимума Л.С.Понтрягина. В задаче 1 для системы (3) из этого принципа следует, что быстрейшее движение может происходить либо по горизонтальным и вертикальным прямым, либо по особому решению - параболе . При движение начинается по вертикальной прямой, при - по горизонтальной, при - по параболе. По каждой из областей и 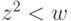проходит не более одного вертикального и одного горизонтального отрезка оптимальной траектории.

Используя теорему о регулярном синтез, можно показать, что оптимальная траектория выглядит следующим образом. Сначала надо выйти на "магистраль" - добраться до параболы по вертикальной или горизонтальной прямой. Затем пройти основную часть пути по магистрали . Если конечная точка лежит под параболой, добраться до нее по горизонтали, сойдя с магистрали. Если она лежит над параболой, заключительный участок траектории является вертикальным отрезком. В частности, в случае оптимальная траектория такова. Сначала надо выйти на магистраль - добраться по вертикальной прямой до параболы. Затем двигаться по магистрали от точки 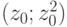до точки . Наконец, по горизонтали выйти в конечную точку.

В задаче 2 из семейства оптимальных траекторий, ведущих из начальной точки 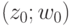в точки луча 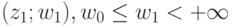, выбирается траектория, требующая минимального времени. При 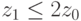оптимально , траектория состоит из вертикального и горизонтального отрезков. При оптимально , траектория проходит по магистрали от точки 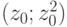до точки . Чем большим объемом знаний 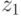надо овладеть, тем большую долю времени надо двигаться по магистрали, отдавая при этом 2/3 времени увеличению умений и 1/3 времени - накоплению знаний.

Полученное для основного участка траектории оптимального обучения значение 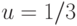можно интерпретировать приблизительно так: на одну лекцию должно приходиться два семинара, на 15 мин. объяснения 30 мин. решения задач. Результаты, полученные в математической модели, вполне соответствуют эмпирическим представлениям об оптимальной организации учебного процесса. Кроме того, модель определяет численные значения доли времени (1/3), идущей на повышение знаний, и доли материала (1/2), излагаемого на заключительных лекциях (без проработки на семинарах).

При движении по магистрали, т.е. в течение основного периода учебного процесса, оптимальное распределение времени между объяснениями и решением задач одно и то же для всех учащихся, независимо от индивидуальных коэффициентов 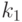и . Этот факт устойчивости оптимального решения показывает возможность организации обучения, оптимального одновременно для всех учащихся. При этом время движения до выхода на магистраль зависит, естественно, от начального положения 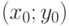и индивидуальных коэффициентов 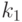и .

Таким образом, модель процесса управления обучением (1) - (2) позволила получить ряд практически полезных рекомендаций, в том числе выраженных в числовой форме. При этом не понадобилось уточнять способы измерения объемов знаний и умений, имеющихся у учащегося. Достаточно было согласиться с тем, что эти величины удовлетворяют качественным соотношениям, приводящим к уравнениям (1) и (2).

Многочисленные модели процессов управления описаны в литературе. Их практическим использованием обычно занимаются информационно-аналитические подразделения, службы контроллинга, качества и надежности, маркетинга и др.

Контрольные вопросы

1. В чем сходство и различие словесных и математических моделей?
2. Согласны ли Вы с моделью лояльности, описанной в подразделе 3.5.1?
3. Опишите основные виды переменных в математических моделях процессов управления.
4. Какие виды математических моделей принятия решений обычно выделяют?
5. В чем суть методологии математического моделирования?

Темы докладов и рефератов

1. Классификация математических моделей процессов управления.
2. Сравнение словесных и математических моделей.
3. Модели процессов управления предприятием.
4. Модели процессов управления качеством.
5. Макроэкономические модели управления.
6. Соотношение задач, моделей, методов и условий применимости.
7. Место принципа максимума Понтрягина среди математических методов оптимального управления.