|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Проблемы устойчивости эконометрических процедур
Робастность статистических процедур
Термин "робастность" (robustness - англ.) образован от robust - крепкий, грубый (англ.). Сравните с названием одного из сортов кофе - robusta. Имеется в виду, что робастные статистические процедуры должны "выдерживать" ошибки, которые теми или иными способами могут попадать в исходные данные или искажать предпосылки используемых вероятностно-статистических моделей.
Термин "робастный" стал популярным в нашей стране в 1970-е годы. Сначала он использовался фактически как сужение термина "устойчивый" на алгоритмы статистического анализа данных классического типа (не включая теорию измерений, статистику нечисловых и интервальных данных). Затем реальная сфера его применения сузилась.
Пусть исходные данные - это выборка, т.е. совокупность независимых одинаково распределенных случайных величин с одной и той же функцией распределения  . Наиболее простая модель изучения устойчивости - это модель засорения
. Наиболее простая модель изучения устойчивости - это модель засорения
 |
( 1) |
Эта модель имеются также моделью Тьюки-Хубера. (Джон Тьюки - американский исследователь, П.Хубер, или Хьюбер - швейцарский ученый) Модель (1) показывает, что с близкой к 1 вероятностью, а именно, с вероятностью 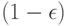 наблюдения берутся из совокупности с функцией распределения
наблюдения берутся из совокупности с функцией распределения  которая предполагается обладающей "хорошими" свойствами. Например, она имеет известный эконометрику вид (хотя бы с точностью до параметров), у нее существуют все моменты, и т.д. Но с малой вероятностью
которая предполагается обладающей "хорошими" свойствами. Например, она имеет известный эконометрику вид (хотя бы с точностью до параметров), у нее существуют все моменты, и т.д. Но с малой вероятностью 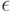 появляются наблюдения из совокупности с "плохим" распределением, например, взятые из распределения Коши, не имеющего математического ожидания, резко выделяющиеся аномальные наблюдения, выбросы.
появляются наблюдения из совокупности с "плохим" распределением, например, взятые из распределения Коши, не имеющего математического ожидания, резко выделяющиеся аномальные наблюдения, выбросы.
Актуальность модели (1) не вызывает сомнений. Наличие засорений (выбросов) может сильно исказить результаты эконометрического анализа данных. Ясно, что если функция распределения элементов выборки имеет вид (1), где первое слагаемое соответствует случайной величине с конечным математическим ожиданием, а второе - такой, для которого математического ожидания не существует (например, если 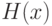 - функция распределения Коши), то для итоговой функций распределения (1) также не существует математического ожидания. Исследователя обычно интересуют характеристики первого слагаемого, но найти их, т.е. освободиться от влияния засорения, не так-то просто. Например, среднее арифметическое результатов наблюдений не будет иметь никакого предела (это - строгое математическое утверждение, вытекающее из того, что математическое ожидание не существует [3]).
- функция распределения Коши), то для итоговой функций распределения (1) также не существует математического ожидания. Исследователя обычно интересуют характеристики первого слагаемого, но найти их, т.е. освободиться от влияния засорения, не так-то просто. Например, среднее арифметическое результатов наблюдений не будет иметь никакого предела (это - строгое математическое утверждение, вытекающее из того, что математическое ожидание не существует [3]).
Существуют различные способы борьбы с засорением. Эмпирическое правило "борьбы с засорениями" при подведении итогов работы команды судей найдено в фигурном катании: наибольшая и наименьшая оценки отбрасываются, а по остальным рассчитывается средняя арифметическая (см. "Эконометрические методы проведения экспертных исследований и анализа оценок экспертов" ). Ясно, что "засорение" окажется среди отброшенных оценок.
Оценивать характеристики и параметры, проверять статистические гипотезы, вообще осуществлять эконометрический анализ данных все чаще рекомендуют на основе эмпирических квантилей (другими словами, порядковых статистик, членов вариационного ряда), отделенных от концов вариационного ряда. Речь идет об использовании статистик типа

Ценой небольшой потери в эффективности избавляемся от засоренности типа описанной в модели (1).
Вариантом этого подхода является переход к сгруппированным данным. Прямая разбивается на интервалы, и вместо количественных значений эконометрик подсчитывает лишь, сколько наблюдений попало в те или иные интервалы. Особое значение приобретают крайние интервалы - к ним относят все наблюдения, которые больше некоторого верхнего порога и меньше некоторого нижнего порога. Любым методам анализа сгруппированных данных резко выделяющиеся наблюдения не страшны.
Можно поставить под сомнение и саму опасность засорения. Дело в том, что практически все реальные величины ограничены. Все лежат на каком-то интервале - от и до. Это совершенно ясно, если речь идет о физическом измерении - все укладывается в шкалу прибора. По-видимому, и для эконометрических измерений наибольшие сложности создают не сверхбольшие помехи, а не засорения, что находятся "на грани" между "интуитивно возможным" и "интуитивно невозможным".
Что же это означает? Если элементы выборки по абсолютной величине не превосходят числа А, то все засорение может сдвинуть среднее арифметическое на величину Если засорение невелико, то и сдвиг мал.
Построена достаточно обширная и развитая теория, посвященная разработке и изучению методов анализа данных в модели (1). С ней можно познакомиться по монографиям [4], [5], [6]. К сожалению, в теории обычно предполагается известной степень засорения , а на практике эта величина неизвестна. Кроме того, теория обычно направлена на защиту от воздействий, якобы угрожающих из бесконечности, а на самом деле реальные данные финитны (сосредоточены на конечных отрезках). Все это объясняет, почему теория робастности, исходящая из модели (1), популярна среди теоретиков, но мало интересна тем, кто анализирует реальные экономические данные.
Рассмотрим несколько более сложную модель. Пусть наблюдаются реализации независимых случайных величин 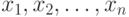 с функциями распределения
с функциями распределения 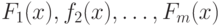 соответственно. Эта модель соответствует гипотезе о том, что в процессе наблюдения (измерения) условия несколько менялись. Естественной представляется модель малых отклонений функций распределений наблюдаемых случайных величин от некоторой "базовой" функции распределения
соответственно. Эта модель соответствует гипотезе о том, что в процессе наблюдения (измерения) условия несколько менялись. Естественной представляется модель малых отклонений функций распределений наблюдаемых случайных величин от некоторой "базовой" функции распределения 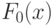 . Множество возможных значений функций распределений наблюдаемых случайных величин описывается следующим образом:
. Множество возможных значений функций распределений наблюдаемых случайных величин описывается следующим образом:
![L((F_1, F_2, \dots, F_n); \epsilon)=\{(F_1, F_2, \dots, F_n): \sup_x |F_i(x)-F_0(x)| < \epsilon, i=1,2, \dots, n]](/sites/default/files/tex_cache/96f9bab58561a8f1b9860fe012c4f6d0.png)
Следующий тип моделей - это введение малой (т.е. слабой) зависимости между рассматриваемыми случайными величинами. Ограничения на взаимную зависимость можно задать разными способами. Пусть 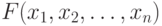 - совместная функция распределения,
- совместная функция распределения,  коэффициент корреляции между
коэффициент корреляции между 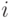 -ой и
-ой и 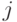 -ой случайными величинами. Множество возможных совместных функций распределения описывается следующим образом:
-ой случайными величинами. Множество возможных совместных функций распределения описывается следующим образом:
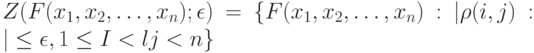
Есть еще целый ряд постановок задач робастности. Если накладывать погрешности непосредственно на результаты наблюдений (измерений), то получаем постановки задач статистики интервальных данных (см. "Эконометрические информационные технологии" ), поскольку каждый результат наблюдения превращается в интервал - исходное значение плюс-минус погрешность.
Разработано много вариантов робастных методов анализа статистических данных (см. монографии [1], [4], [5] [6]). Иногда говорят, что робастные методы позволяют использовать информацию о том, что реальные наблюдения лежат "около" тех или иных параметрических семейств, например, нормальных. В этом, дескать, их преимущество по сравнению с непараметрическими методами, которые предназначены для анализа данных из всех возможных распределений. Однако количественных подтверждений этих уверений любителей робастных методов обычно не удается найти.

