Эллиптические кривые в GF(p)

Наша предыдущая группа эллиптической кривой использовала вещественное поле для вычислений сложения точек. Криптография требует модульной арифметики. Мы определили группу эллиптической кривой с операцией сложения, но операция на координатах с точками в данном случае есть операция в GF(p) с p> 3. В модульной арифметике точки на кривой не представляют графы, как это можно было видеть на предыдущих рисунках, но сохраняются те же самые основные концепции. Мы используем ту же самую операцию сложения, но с вычислением по модулю p. В результате мы получаем эллиптическую кривую E_p (a, b), где p определяет модуль, и b — коэффициент уравнения y² = x³ + ax + b. Обратите внимание, что хотя значение x в этом случае от 0 до p, обычно не все точки находятся на кривой.

Нахождение инверсии

Инверсия точки (x, y) равна (x, – y), где (–y) — аддитивная инверсия y. Например, если p = 13, инверсия (4, 2) равна (4, 11).

Нахождение точек на кривой

Алгоритм 15.7 показывает программу в псевдокоде для нахождения точек на кривой E_p (a, b).

                \[
                \tt\parindent0pt

Elliptic\_points (p, a, b)              // $p$-модуль

\{ 

$x \gets  0$

while ($x < p$)

\{ 

$w \gets  (x^{3} + ax + b) \mod p$\ \ \            //$w$ – это $y^{2}$

if ($w$ – целое значение квадратного корня в $Z_{p}$)  выход $((x, \sqrt w )(x, - \sqrt w ))$

$x \gets  x + 1$

\} 

\}	
                \]
            

Пример 15.6

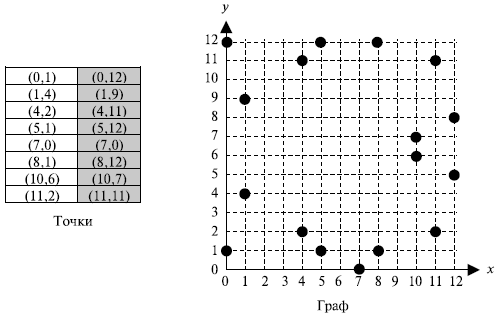
Определите эллиптическую кривую E₁₃ (1, 1) по уравнению y² = x³ + x + 1 и вычислите по модулю 13. Точки на кривой могут быть найдены, как показано на рис. 15.5.

Рис. 15.5. Точки на эллиптической кривой в поле GF (p)

Обратите внимание на следующее:

а. Некоторые значения y² не имеют квадратного корня по модулю 13. Они не являются точками на этой эллиптической кривой. Например, точки x = 2, x = 3, x = 6 и x = 9 не находятся на кривой.

б. Каждая точка, определенная на кривой, имеет инверсию. Инверсии перечислены как пары. Заметим, что (7, 0) — инверсия самой себя.

в. Обратите внимание, что для пары обратных точек значения y — аддитивные инверсии друг друга в Z_p. Например, 4 и 9 — аддитивные инверсии в Z₁₃. Так что мы можем сказать, что если 4 — это значение y, то 9— это значение (–y).

г. Инверсии находятся на тех же самых вертикальных линиях.

Сложение двух точек

Мы используем группу эллиптической кривой, определенную ранее, но вычисления сделаны в GF (p). Вместо вычитания и деления мы применяем аддитивные и мультипликативные инверсии.

Пример 15.7

Сложим две точки в примере 15.6, R = P + Q, где P = (4, 2) и Q = (10,6).

а. X = (6 – 2) x (10 – 4) ^-1 mod 13 = 4 x 6^-1 mod 13 != 5 mod 13.

б. x = (5² – 4 – 10) mod 13 = 11 mod 13.

в. y = [5 (4 – 11) – 2] mod 13 = 2 mod 13.

г . R = (11, 2) является точкой на кривой в примере 15.6.

Умножение точки на константу

В арифметике умножение числа на константу k означает прибавление числа само к себе k раз. Здесь ситуация та же самая. Умножение точки P на эллиптической кривой на константу k означает прибавление точки P к себе k раз. Например, в E₁₃ (1, 1), если точка (1, 4) умножается на 4, результат есть точка (5, 1). Если точка (8,1) умножается на 3, результат — точка (10, 7).

Эллиптические кривые в GF(2 в степени n)

Вычисление в группе эллиптической кривой может быть определено в поле GF(2ⁿ). В соответствии с лекциями 5-6, где мы говорили, что элементы множества в этом поле — n -битовые слова, которые можно интерпретировать как полиномы с коэффициентом в GF(2), сложение и умножение этих элементов такое же, как сложение и умножение полиномов. Для того чтобы определить эллиптическую кривую в GF(2ⁿ), необходимо только изменить кубическое уравнение. Общее уравнение

y² + xy = x³ + ax² + b

где \[ b \ne 0 \] . Обратите внимание, что значение x, y, a и b — полиномы, представляющие n -битовые слова.

Нахождение инверсии

Если P = (x, y), то (–P) = (x, x + y).

Нахождение точек на кривой

Мы можем написать алгоритм для нахождения точек на кривой, используя генераторы для полиномов, которые рассматривали в лекциях 9-10. Но разработку этого алгоритма оставляем как упражнение. Далее следует очень тривиальный пример.

Пример 15.8

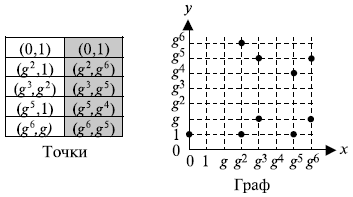
Мы выбираем GF (2 ³) с элементами (0,1, g, g², g³, g ⁴, g⁵, g⁶), использующими неприводимый полином f (x) = x³ + x +1. Этому соответствует полином g³ + g +1 = 0 или g³ = g + 1. Другие степени g могут быть вычислены, как это показано ниже.

Используя эллиптическую кривую y² + xy = x³ + g³x² + 1, a = g³ и b = 1, мы можем найти точки на этой кривой, как это показано на рисунке 15.6.

Рис. 15.6. Точки на эллиптической кривой в GF (2 в степени n)

Сложение двух точек

Правила для сложения точек в GF(2ⁿ) немного отличаются от правил GF(p).

1. Если P = (x₁, y₁), Q = (x₂, y₂), \[ Q \ne -P \] , \[ Q \ne P \] , то R = (x₃, y₃) = P + Q может быть найден как

2.Если Q = P, то R = P + P (или R = 2P ) и может быть найден как

Пример 15.9

Пусть нам надо найти R = P + Q, где P = (0,1) и Q = (g²,1). Мы имеем \[ \lambda = 0 \] и R = (g⁵, g⁴).

Пример 15.10

Пусть нам надо найти R = 2P, где P = (g²,1). Мы имеем \[ \lambda =g^{2} +1 /g^{2} = g^{2}+ g^{5}= g +1 \] и R = (g⁶, g⁵).

Умножение точек на константу

Для того чтобы умножить точку на константу, точки должны складываться непрерывно согласно правилу R = 2P.