|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
Параметры системы управления запасами.Под параметрами системы управления запасами в настоящей работе понимаются все известные характеристики системы, ее окружения, значения внешних и внутренних факторов, которые влияют на выбор стратегии управления запасами и входят в выражения для ограничений или функции затрат. В рассматриваемой нестационарной системе управления запасами имеются как стационарные, так и нестационарные параметры.
Нестационарные параметры зависят от времени и задаются функциональными зависимостями вида 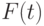 . Так, для исследуемой системы управления запасами нестационарным параметром является величина спроса
. Так, для исследуемой системы управления запасами нестационарным параметром является величина спроса 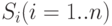 .
.
Стационарные параметры не зависят от времени и задаются константами (например, объем склада  ).
).
Ограничения системы управления запасами.Под ограничениями в рассматриваемой схеме понимаются условия, которым должна удовлетворять система управления запасами в каждый момент времени. Все ограничения задаются в виде неравенств вида:
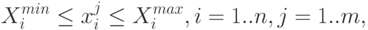
где 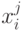 - значение контролируемого показателя системы в момент времени
- значение контролируемого показателя системы в момент времени  при реализации стратегии
при реализации стратегии  ;
;
 - наименьшее допустимое значение контролируемого показателя системы в момент времени
- наименьшее допустимое значение контролируемого показателя системы в момент времени  ;
;
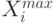 - наибольшее допустимое значение контролируемого показателя системы в момент времени
- наибольшее допустимое значение контролируемого показателя системы в момент времени  .
.
Если параметры  и
и  - стационарны (не зависят от времени), то аналогичное неравенство будет выглядеть так:
- стационарны (не зависят от времени), то аналогичное неравенство будет выглядеть так: 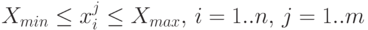 .
.
увеличить изображение
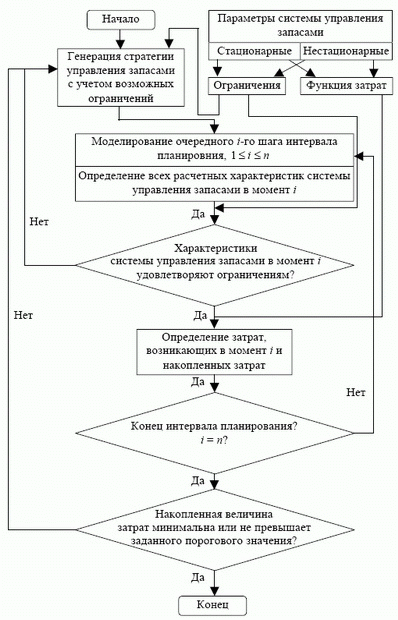
Рис. 4.11. Схема определения оптимальной стратегии управления запасами нестационарной детерминированной системы
Функция затрат.Под функцией затрат в настоящей задаче понимается функция вида:
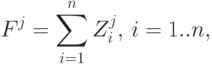
где 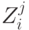 - величина совокупных затрат, возникающих в системе момент времени
- величина совокупных затрат, возникающих в системе момент времени  при реализации стратегии
при реализации стратегии 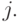
Моделирование очередного i-го шага функционирования складской системы в плановом периоде  представляет собой определение всех необходимых расчетных и контролируемых характеристик складской системы в момент времени
представляет собой определение всех необходимых расчетных и контролируемых характеристик складской системы в момент времени  при реализации стратегии управления запасами
при реализации стратегии управления запасами 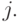
Таким образом, работа схемы определения оптимальной стратегии управления запасами представляет собой моделирование функционирования складской системы предприятия при различных возможных стратегиях управления запасами  . Если при моделировании каждого шага
. Если при моделировании каждого шага 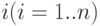 функционирования складской системы предприятия при реализации стратегии
функционирования складской системы предприятия при реализации стратегии  все контролируемые характеристики системы удовлетворяют ограничениям, то такая стратегия является допустимой. Для допустимых стратегий определяется величина функции затрат
все контролируемые характеристики системы удовлетворяют ограничениям, то такая стратегия является допустимой. Для допустимых стратегий определяется величина функции затрат  , которая складывается из сумм затрат, возникающих на каждом шаге моделирования
, которая складывается из сумм затрат, возникающих на каждом шаге моделирования  стратегии
стратегии 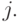 Работа схемы определения оптимальной стратегии управления запасами заканчивается, когда определены функции затрат
Работа схемы определения оптимальной стратегии управления запасами заканчивается, когда определены функции затрат  для всех допустимых стратегий
для всех допустимых стратегий  . Оптимальной стратегией управления запасами на период
. Оптимальной стратегией управления запасами на период  в рассматриваемой складской системе будет та стратегия
в рассматриваемой складской системе будет та стратегия 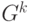 , для которой
, для которой

где  - множество допустимых стратегий управления запасами для рассматриваемой складской системы.
- множество допустимых стратегий управления запасами для рассматриваемой складской системы.
В случаях, когда известна предпочтительная нижняя граница величины затрат  , работа схемы прекращается в тот момент, как только находится допустимая стратегия
, работа схемы прекращается в тот момент, как только находится допустимая стратегия 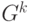 , для которой
, для которой  .
.
Представленная выше схема позволяет из множества возможных стратегий выбрать оптимальную, дающую минимальную величину затрат на создание и поддержание запасов в планируемом периоде  при условии соответствия имеющимся ограничениям.
при условии соответствия имеющимся ограничениям.
Постановка оптимизационной задачи определения оптимальной стратегии управления запасами для нестационарной детерминированной системы.Выше было показано, что общее количество стратегий
( 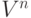 ) при длительном интервале планирования
) при длительном интервале планирования  и большом количестве вариантов объема поставки продукции
и большом количестве вариантов объема поставки продукции  очень велико. Поэтому даже максимально сузив круг исследуемых стратегий с учетом возможных ограничений и используя средства вычислительной техники потребуются значительные затраты времени для нахождения оптимальной стратегии путем перебора всех допустимых стратегий в конкретных условиях задачи. Если же необходимо пересчитывать оптимальную стратегию управления запасами постоянно и непрерывно, то нахождение оптимального решения с помощью полного перебора допустимых стратегий вообще теряет смысл, так как за время вычислений найденное решение потеряет свою актуальность.
очень велико. Поэтому даже максимально сузив круг исследуемых стратегий с учетом возможных ограничений и используя средства вычислительной техники потребуются значительные затраты времени для нахождения оптимальной стратегии путем перебора всех допустимых стратегий в конкретных условиях задачи. Если же необходимо пересчитывать оптимальную стратегию управления запасами постоянно и непрерывно, то нахождение оптимального решения с помощью полного перебора допустимых стратегий вообще теряет смысл, так как за время вычислений найденное решение потеряет свою актуальность.
Таким образом, необходим алгоритм решения исследуемой оптимизационной задачи. Чтобы определить метод и алгоритм решения задачи - необходимо ее формализовать. Исследуемая задача - это задача выбора в заданном множестве элемента, удовлетворяющего тем или иным критериям, поэтому является предметом исследования операций. Любая задача исследования операций включает описание множества допустимых решений (задается с помощью ограничений) и критерия оптимальности (целевой функции), на основании которого проводятся сравнительная оценка допустимых решений и выбор оптимального решения [5]. Для описания ограничений и целевой функции оптимизационной задачи перечислим исходные параметры исследуемой системы управления запасами.
Параметры системы управления запасами.В исследуемой нестационарной детерминированной системе управления запасами, описанной выше, заданы следующие параметры:
- Известны границы и продолжительность периода времени, на который будет рассчитываться оптимальная стратегия управления запасами:
![T_{общ} = [ t_{н}; t_{к}],](/sites/default/files/tex_cache/a9dd9f8992ef65935de4e3840b071d7f.png)
где
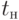 ,
,  - начальный и конечный моменты времени соответственно;
- начальный и конечный моменты времени соответственно;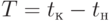 - продолжительность периода времени.
- продолжительность периода времени.Будем считать время дискретной величиной с шагом
 (день, неделя и т. п.). Тогда период планирования
(день, неделя и т. п.). Тогда период планирования ![T_{общ} = [t_{н}; t_{к}]](/sites/default/files/tex_cache/2c5f4bc61db665de0959e27f6015e85f.png) можно представить в виде последовательности дискретных интервалов (или моментов) времени -
можно представить в виде последовательности дискретных интервалов (или моментов) времени - 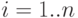 , где
, где 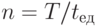 - количество единичных интервалов времени в отчетном периоде.
- количество единичных интервалов времени в отчетном периоде.В дальнейшем будем считать единицей учета времени дискретный интервал времени
 (
( 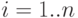 ).
). - Известна потребность в продукции на планируемый интервал времени
 (нестационарный параметр):
(нестационарный параметр): 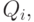
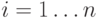 .
. - Если в системе не допускается дефицит товара на складе, то необходимо постоянно иметь определенный уровень запаса (страховой запас), чтобы избежать дефицита товара из-за влияния непредвиденных случайных факторов. Величина страхового запаса также может быть нестационарной и задаваться функцией:
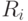 ,
, 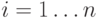 .
. - Известна стоимость единицы продукции:
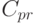 .
. - Известен минимальный, максимальный объем поставки, а также стандартный объем упаковки (коробки, паллеты, и т. п.):
 - минимальный объем поставки (в единицах продукции),
- минимальный объем поставки (в единицах продукции), - максимальный объем поставки (в единицах продукции),
- максимальный объем поставки (в единицах продукции),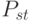 - размер стандартной упаковки (в единицах продукции).
- размер стандартной упаковки (в единицах продукции). - Известен минимальный возможный интервал времени между соседними поставками продукции:
 . Это ограничение вызвано тем, что для большинства предприятий частота поставок товара поставщиком, а также частота приемки товара на склад ограничены техническими возможностями.
. Это ограничение вызвано тем, что для большинства предприятий частота поставок товара поставщиком, а также частота приемки товара на склад ограничены техническими возможностями. - Известна емкость транспортной единицы, а также стоимость перевозки груза этой транспортной единицей:
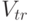 - емкость транспортной единицы (в единицах продукции);
- емкость транспортной единицы (в единицах продукции);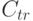 - стоимость одной перевозки одной транспортной единицей.
- стоимость одной перевозки одной транспортной единицей. - Известна емкость склада:
 (в единицах продукции).
(в единицах продукции). - Известна стоимость хранения единицы продукции на складе в единицу времени (переменная составляющая всех складских расходов):
 .
. - Известна величина утраченной выгоды из-за связывания оборотных средств в запасе (задается как доля стоимости хранимого запаса в единицу времени):
 . Величина утраченной выгоды равна величине возможного гарантированного дохода при альтернативном вложении денежных средств (например, сумме банковского процента):
. Величина утраченной выгоды равна величине возможного гарантированного дохода при альтернативном вложении денежных средств (например, сумме банковского процента):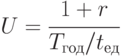
где
 - величина банковского годового процента;
- величина банковского годового процента;  - величина годового периода времени.
- величина годового периода времени. - Известна величина штрафа из-за дефицита продукции на складе, выраженная в процентах к сумме дефицита в единицу времени:
 .
.
Формирование целевой функции определения оптимальной стратегии управления запасами.Цель исследуемой оптимизационной задачи - нахождение оптимальной стратегии управления запасами, дающей минимальные совокупные затраты на создание и пополнение запаса за период планирования  . Поэтому в качестве целевой функции выбрана функция затрат:
. Поэтому в качестве целевой функции выбрана функция затрат:
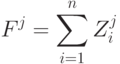
В процессе реализации какойлибо стратегии управления запасами 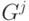 на предприятии возникают следующие виды затрат:
на предприятии возникают следующие виды затрат:
- транспортные издержки (стоимость доставки продукции на склад предприятия);
- затраты на хранение (стоимость эксплуатации склада);
- затраты, вызванные связыванием оборотных средств в товарном запасе;
- затраты, возникающие на предприятии из-за дефицита продукции на складе;
- затраты на заработную плату персонала;
- накладные расходы предприятия.
От выбора стратегии управления запасами зависят только четыре первых вида потерь, поэтому именно они включаются в уравнение целевой функции. Таким образом, целевую функцию можно записать в следующем виде:
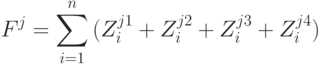
где  - величина транспортных затрат, возникающих в момент
- величина транспортных затрат, возникающих в момент  при реализации стратегии управления запасами
при реализации стратегии управления запасами  ;
;
 - величина затрат на хранение, возникающая в момент
- величина затрат на хранение, возникающая в момент  при реализации стратегии управления запасами
при реализации стратегии управления запасами  ;
;
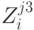 - величина затрат, возникающих в момент
- величина затрат, возникающих в момент  при реализации стратегии управления запасами
при реализации стратегии управления запасами  , вызванных связыванием оборотных средств;
, вызванных связыванием оборотных средств;
 - величина затрат, возникающих в момент
- величина затрат, возникающих в момент  при реализации стратегии управления запасами
при реализации стратегии управления запасами  , вызванных наличием дефицита на складе.
, вызванных наличием дефицита на складе.
Введем следующие положения:
- любая стратегия
 задается последовательностью значений
задается последовательностью значений  ::
::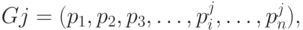
где
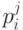 - объем поставки продукции на предприятие в момент времени
- объем поставки продукции на предприятие в момент времени  (
( 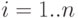 ), при реализации стратегии
), при реализации стратегии  ;
; - текущая величина запаса продукции в момент i при реализации стратегии
 определяется как:
определяется как:
Величина транспортных затрат  в момент времени
в момент времени  определяется как:
определяется как:
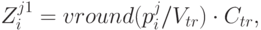
где  - функция округления аргумента в большую сторону до целого. Величина затрат на хранение
- функция округления аргумента в большую сторону до целого. Величина затрат на хранение  в момент времени
в момент времени  определяется как:
определяется как:

Величина затрат, вызванных связыванием оборотных средств 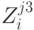 в момент времени
в момент времени  определяется как:
определяется как:
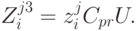
Величина затрат, вызванных наличием дефицита на складе  в момент времени
в момент времени  определяется как:
определяется как:
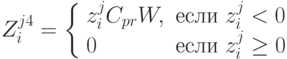
Поскольку все затраты в течение планового периода разнесены во времени, то их необходимо приводить к единому моменту времени (например, к началу планового периода) с учетом дисконтфактора. Таким образом, если 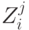 - сумма всех затрат, возникающих в момент времени
- сумма всех затрат, возникающих в момент времени  , то общие затраты за весь плановый период
, то общие затраты за весь плановый период  будут подсчитываться согласно:
будут подсчитываться согласно:

где 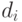 - величина коэффициента дисконтирования в момент
- величина коэффициента дисконтирования в момент  , приводящего сумму затрат
, приводящего сумму затрат 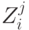 к начальному моменту времени:
к начальному моменту времени:
В развернутом виде целевая функция задачи нахождения оптимальной стратегии для нестационарной детерминированной системы управления запасами будет выглядеть следующим образом:
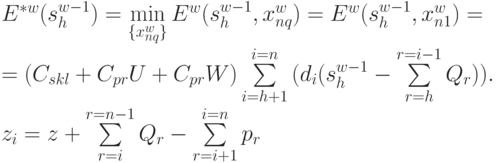
Формирование системы ограничений оптимизационной задачи.Все ограничения в задаче об оптимальном управлении запасами можно классифицировать на ограничения:
- поставщика;
- рынка;
- внутренние.
В исследуемой задаче имеют место ограничения поставщика и внутренние ограничения. Ограничения поставщика.
Объем поставки не может быть меньше минимальной партии, не должен превышать максимальную партию и должен быть кратен стандартной упаковке :
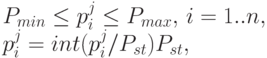
где  - функция извлечения целой части аргумента. Внутренние ограничения:
- функция извлечения целой части аргумента. Внутренние ограничения:
- уровень запаса не должен превышать вместимость склада, а также не должен опускаться ниже уровня страхового запаса (если рассматривается бездефицитная модель):

- ограничен минимальный интервал времени между соседними поставками товара:

где
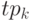 - момент времени поставки
- момент времени поставки  ,
,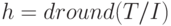 - максимальное количество поставок в планируемом периоде
(
- максимальное количество поставок в планируемом периоде
(  - функция округления аргумента до ближайшего меньшего целого).
- функция округления аргумента до ближайшего меньшего целого).
Таким образом, можно сформулировать математическую постановку задачи оптимального управления запасами:
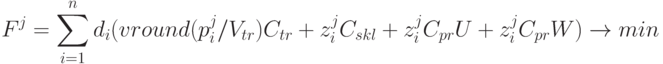 |
( 4.16) |
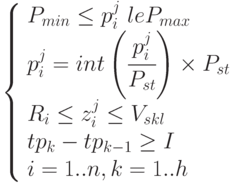 |
( 4.17) |
 |
( 4.18) |
(балансовое условие оптимизационной задачи).
Выбор метода решения оптимизационной задачи нахождения оптимальной стратегии. Описанная выше оптимизационная задача является многошаговой (динамической) задачей принятия решений в условиях определенности, поэтому для ее решения будут использоваться методы исследования операций, в частности, метод динамического программирования (как наиболее часто используемый на сегодня метод решения рассматриваемых динамических задач) [1], [2], [3], [5], [6].
Важные особенности метода динамического программирования:
- Функция затрат
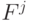 не обязана быть дифференцируемой и может задаваться таблично или алгоритмически.
не обязана быть дифференцируемой и может задаваться таблично или алгоритмически. - Гарантируется получение глобального минимума, причем наличие локальных минимумов не создает никаких трудностей.
- Дополнительные ограничения только облегчают получение решения, поскольку сужают пространство поиска.
- Используя решения, полученные на предыдущих этапах, можно решить задачу с меньшим числом периодов.
- Метод может быть обобщен на многоресурсные задачи (в частности, с предварительным распределением затрат по уровням).