|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Хэш-функции и аутентификация сообщений. Часть 1
Простые хэш-функции
Все хэш-функции выполняются следующим образом. Входное значение (сообщение, файл и т.п.) рассматривается как последовательность n-битных блоков. Входное значение обрабатывается последовательно блок за блоком, и создается m-битное значение хэш-кода.
Одним из простейших примеров хэш-функции является побитовый XOR каждого блока:
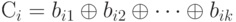
Где
| Сi - i-ый бит хэш-кода, 1 <= i <= n. |
| k - число n-битных блоков входа. |
| bij - i-ый бит в j-ом блоке. |
 - операция XOR. - операция XOR. |
В результате получается хэш-код длины n, известный как продольный избыточный контроль. Это эффективно при случайных сбоях для проверки целостности данных.
Часто при использовании подобного продольного избыточного контроля для каждого блока выполняется однобитный циклический сдвиг после вычисления хэш-кода. Это можно описать следующим образом.
- Установить n-битный хэш-код в ноль.
- Для каждого n-битного блока данных выполнить следующие операции:
Это даст эффект "случайности" входа и уничтожит любую регулярность, которая присутствует во входных значениях.
Хотя второй вариант считается более предпочтительным для обеспечения целостности данных и предохранения от случайных сбоев, он не может использоваться для обнаружения преднамеренных модификаций передаваемых сообщений. Зная сообщение, атакующий легко может создать новое сообщение, которое имеет тот же самый хэш-код. Для этого следует подготовить альтернативное сообщение и затем присоединить n-битный блок, который является хэш-кодом нового сообщения, и блок, который является хэш-кодом старого сообщения.
Хотя простого XOR или ротационного XOR ( RXOR ) недостаточно, если целостность обеспечивается только зашифрованным хэш-кодом, а само сообщение не шифруется, подобная простая функция может использоваться, когда все сообщение и присоединенный к нему хэш-код шифруются. Но и в этом случае следует помнить о том, что подобная хэш-функция не может проследить за тем, чтобы при передаче последовательность блоков не изменилась. Это происходит в силу того, что данная хэш-функция определяется следующим образом: для сообщения, состоящего из последовательности 64-битных блоков Х1, Х2,..., ХN, определяется хэш-код С как поблочный XOR всех блоков, который присоединяется в качестве последнего блока:
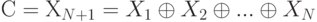
Затем все сообщение шифруется, включая хэш-код, в режиме СВС для создания зашифрованных блоков Y1, Y2, ..., YN+1. По определению СВС имеем:
![Х_{1} = IV \oplus D_{K} [Y_{1}]\\
Х_{i} = Y_{i-1} \oplus D_{K} [Y_{i}]\\
Х_{N+1} = Y_{N} \oplus D_{K} [Y_{N+1}]](/sites/default/files/tex_cache/77b5d718be73f5956eb17577f0370fe5.png)
![Х_{N+1} = X_{1} \oplus X_{2} \oplus . . . \oplus X_{N} = \\
(IV \oplus D_{K} [Y_{1}]) \oplus (Y_{1} \oplus D_{K} [Y_{2}]) \oplus . . . \oplus \\
(Y_{N-1} \oplus D_{K} [Y_{N}])](/sites/default/files/tex_cache/e1573a2b109b5741d84239873fde3011.png)
Так как слагаемые в предыдущем равенстве могут вычисляться в любом порядке, следовательно, хэш-код не будет изменен, если зашифрованные блоки будут переставлены.
Первоначальный стандарт, предложенный NIST, использовал простой XOR, который применялся к 64-битным блокам сообщения, затем все сообщение шифровалось, используя режим СВС.
"Парадокс дня рождения"
Прежде чем рассматривать более сложные хэш-функции, необходимо проанализировать одну конкретную атаку на простые хэш-функции.
Так называемый " парадокс дня рождения " состоит в следующем.
Предположим, количество выходных значений хэш-функции Н равно n.
Каким должно быть число k, чтобы для конкретного значения X и
значений Y1,  , Yk вероятность того, что хотя бы для одного Yi
выполнялось равенство
, Yk вероятность того, что хотя бы для одного Yi
выполнялось равенство
H (X) = H (Y)
была бы больше 0,5.
Для одного Y вероятность того, что H (X) = H (Y), равна 1/n.
Соответственно, вероятность того, что 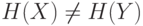 , равна 1 - 1/n.
, равна 1 - 1/n.
Если создать k значений, то вероятность того, что ни для одного из них не будет совпадений, равна произведению вероятностей, соответствующих одному значению, т.е. (1 - 1/n)k.
Следовательно, вероятность, по крайней мере, одного совпадения равна
1 - (1 - 1/n)k
По формуле бинома Ньютона
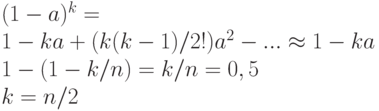
Таким образом, мы выяснили, что для m-битового хэш-кода достаточно выбрать 2m-1 сообщений, чтобы вероятность совпадения хэш-кодов была больше 0,5.
Теперь рассмотрим следующую задачу: обозначим P (n, k) вероятность того, что в множестве из k элементов, каждый из которых может принимать n значений, есть хотя бы два с одинаковыми значениями. Чему должно быть равно k, чтобы P (n, k) была бы больше 0,5?
Число различных способов выбора элементов таким образом, чтобы при этом не было дублей, равно
n(n-1) ... (n-k+1)=n!/(n-k)!
Всего возможных способов выбора элементов равно
nk
Вероятность того, что дублей нет, равна
n!/(n-k)!nk
Вероятность того, что есть дубли, соответственно равна
1 - n!/(n-k)!nk
P (n, k) = 1 - n! / ((n-k)! x nk) = 1 - (n x (n-1) x ... x (n-k-1)) / nk = 1 - [ (n-1)/n x (n-2)/n x ... x (n-k+1)/n] = 1 - [(1- 1/n) x (1 - 2/n) x ... x (1 - (k-1)/n)]
Известно, что
![1 - x <= e^{-x}\\
P (n, k) > 1 - [e^{-1/n} x e^{-2}/n x ... x e^{-k}/n]\\
P (n, k) > 1 - e^{-k(k-1)/n}\\
1/2 = 1 - e^{-k(k-1)/n}\\
2 = e^{k(k-1)/n}\\
ln 2 = k (k-1) / 2n\\
k (k-1) \approx k^{2}\\
k = (2n x ln 2)^{1/2} = 1,17 n^{1/2} \approx n^{1/2}](/sites/default/files/tex_cache/fa5c5b544f152780cae90b19e5dea2be.png)
Если хэш-код имеет длину m бит, т.е. принимает 2m значений, то

Подобный результат называется "парадоксом дня рождения", потому что в соответствии с приведенными выше рассуждениями для того, чтобы вероятность совпадения дней рождения у двух человек была больше 0,5, в группе должно быть всего 23 человека. Этот результат кажется удивительным, возможно, потому, что для каждого отдельного человека в группе вероятность того, что с его днем рождения совпадет день рождения кого-то другого в группе, достаточно мала.
Вернемся к рассмотрению свойств хэш-функций. Предположим, что используется 64-битный хэш-код. Можно считать, что это вполне достаточная и, следовательно, безопасная длина для хэш-кода. Например, если зашифрованный хэш-код С передается с соответствующим незашифрованным сообщением М, то противнику необходимо будет найти М' такое, что
Н (М') = Н (М)
для того, чтобы подменить сообщение и обмануть получателя. В среднем противник должен перебрать 263 сообщений для того, чтобы найти такое, у которого хэш-код равен перехваченному сообщению.
Тем не менее, возможны различного рода атаки, основанные на "парадоксе дня рождения". Возможна следующая стратегия:
- Противник создает 2m/2 вариантов сообщения, каждое из которых имеет некоторый определенный смысл. Противник подготавливает такое же количество сообщений, каждое из которых является поддельным и предназначено для замены настоящего сообщения.
- Два набора сообщений сравниваются в поисках пары сообщений, имеющих одинаковый хэш-код. Вероятность успеха в соответствии с "парадоксом дня рождения" больше, чем 0,5. Если соответствующая пара не найдена, то создаются дополнительные исходные и поддельные сообщения до тех пор, пока не будет найдена пара.
- Атакующий предлагает отправителю исходный вариант сообщения для подписи. Эта подпись может быть затем присоединена к поддельному варианту для передачи получателю. Так как оба варианта имеют один и тот же хэш-код, будет создана одинаковая подпись. Противник будет уверен в успехе, даже не зная ключа шифрования.
Таким образом, если используется 64-битный хэш-код, то необходимая сложность вычислений составляет порядка 232.
В заключение отметим, что длина хэш-кода должна быть достаточно большой. Длина, равная 64 битам, в настоящее время не считается безопасной. Предпочтительнее, чтобы длина составляла порядка 100 битов.
Использование цепочки зашифрованных блоков
Существуют различные хэш-функции, основанные на создании цепочки зашифрованных блоков, но без использования секретного ключа. Одна из таких хэш-функций была предложена Рабином. Сообщение М разбивается на блоки фиксированной длины М1, М2, . . . , МN и используется алгоритм симметричного шифрования, например DES, для вычисления хэш-кода G следующим образом:
Н0 = начальное значение Нi = EMi [Hi-1] G = HN
Это аналогично использованию шифрования в режиме СВС, но в данном случае секретного ключа нет. Как и в случае любой простой хэш-функции, этот алгоритм подвержен "атаке дня рождения", и если шифрующим алгоритмом является DES и создается только 64-битный хэш-код, то система считается достаточно уязвимой.
Могут осуществляться другие атаки типа "дня рождения", которые возможны даже в том случае, если противник имеет доступ только к одному сообщению и соответствующему ему зашифрованному хэш-коду и не может получить несколько пар сообщений и зашифрованных хэш-кодов. Возможен следующий сценарий: предположим, что противник перехватил сообщение с аутентификатором в виде зашифрованного хэш-кода, и известно, что незашифрованный хэш-код имеет длину m битов. Далее противник должен выполнить следующие действия:
- Используя описанный выше алгоритм, вычислить незашифрованный хэш-код G.
- Создать поддельное сообщение в виде Q1, Q2, . . . , QN-2.
- Вычислить Нi = EQi[Hi-1] для 1 <= i <= N-2.
- Создать 2m/2 случайных блока Х и для каждого такого блока Х вычислить ЕХ[HN-2]. Создать дополнительно 2m/2 cлучайных блока Y и для каждого блока Y вычислить DY[G], где D - дешифрующая функция, соответствующая Е. Основываясь на "парадоксе дня рождения" можно сказать, что с высокой степенью вероятности эта последовательность будет содержать блоки Х и Y такие, что ЕХ[HN-2] = DY[Y].
- Создать сообщение Q1, Q2, . . . , QN-2, X, Y. Это сообщение имеет хэш-код G и, следовательно, может быть использовано вместе с зашифрованным аутентификатором.
Эта форма атаки известна как атака "встреча посередине". В различных исследованиях предлагаются более тонкие методы для усиления подхода, основанного на цепочке блоков. Например, Девис и Прайс описали следующий вариант:
![H_{i} = E_{Mi} [H_{i-1}] \oplus H_{i-1}](/sites/default/files/tex_cache/d7fb8d7cd754e86edef4402f17901432.png)
Возможен другой вариант:
![H_{i} = E_{Hi-1} [M_{i}] \oplus M_{i}](/sites/default/files/tex_cache/c61c23c07c86576d584548efed250699.png)
Однако обе эти схемы также имеют уязвимости при различных атаках. В более общем случае, можно показать, что некоторая форма "атаки дня рождения" имеет успех при любом хэш-алгоритме, включающем использование цепочки шифрованных блоков без применения секретного ключа.
Дальнейшие исследования были направлены на поиск других подходов к созданию функций хэширования.

