НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 15: Криптосистемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать программу

15.4. Рекомендованная литература

Для более детального изучения положений, обсужденных в этой лекции, мы рекомендуем нижеследующие книги и сайты. Пункты, указанные в скобках, показаны в списке ссылок в конце книги.

Книги

Криптографическая система RSА рассматривается в [Sti06], [Sta06], [PHS03], [Vau06], [TW06] и [Mao04]. Криптосистемы Рабина и Эль-Гамаля — в [Sti06] и [Mao04]. Криптография эллиптической кривой — в [Sti06], [Eng99] и [Bla03].

Сайты

Следующие сайты дают больше информации о темах, рассмотренных в этой лекции.

15.5. Итоги

Есть два способа достигнуть информационной безопасности: криптография с симметричными ключами и криптография с асимметричными ключами. Эти два способа существуют параллельно и дополняют друг друга; преимущества одного могут дать компенсацию недостаткам другого.
Концептуальные различия между этими двумя способами базируются на том, как они сохраняют секретность. В криптографии с симметричными ключами секретность должна быть разделена между двумя объектами; в криптографии с асимметричными ключами секретность персональная (неразделенная).
Криптография с симметричными ключами базируется на подстановке и перестановке символов; криптография с асимметричными ключами базируется на применении математических функций к числам.
Криптография с асимметричными ключами использует два отдельных ключа: один секретный и один открытый. Шифрование и дешифрование можно представлять себе как запирание и отпирание замков ключами. Замок, который заперт открытым ключом, можно отпереть только соответствующим секретным ключом.
В криптографии с асимметричным ключом ответственность обеспечения безопасности находится, главным образом, на плечах приемника (Боб), который должен создать два ключа: один секретный и один открытый. Боб несет ответственность за секретный ключ. Открытый ключ может быть распространен сообществу через канал распределения открытого ключа.
В отличие от криптографии с симметричными ключами, в криптографии с асимметричным ключом исходный текст и зашифрованный текст обрабатываются как целые числа. Сообщение должно кодироваться как целое число (или множество целых чисел) перед шифрованием; целое число (или множество целых чисел) должно быть расшифровано в сообщение после дешифрования. Криптография с асимметричным ключом обычно используется, чтобы зашифровать или расшифровывать маленькие сообщения, такие как ключ шифра для криптографии с симметричными ключами.
Главная идея криптографии с асимметричным ключом — понятие "лазейка" в односторонней функции (TOWF), которая является такой функцией, что f вычисляется просто, а f^-1 вычислить невозможно (в смысле сложности вычислений), если не используется лазейка.
Блестящая идея относительно криптографии общедоступного ключа принадлежит Меркелю и и Хеллману – это ранцевая криптосистема . Когда нам говорят, какие элементы из заранее заданного множества чисел находятся в рюкзаке, мы можем легко вычислить сумму чисел; когда нам сообщают сумму, трудно сказать, какие элементы находятся в рюкзаке, если он не заполнен элементами сверхвозрастающего множества.
Самый общий алгоритм общедоступного ключа — криптографическая система RSА. RSA использует два числа e и d, где e — общедоступный ключ, а d является частным (секретным). Алиса использует C = P^e mod n для того, чтобы создать зашифрованный текст C из исходного текста P ; Боб использует P = С^d mod n, чтобы извлечь исходный текст, переданный Алисой.
RSA применяет две алгебраических структуры: кольцо и группа. Шифрование и дешифрование выполняются с использованием коммутативного кольца 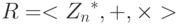$R = < {Z_n}^*, + , \times >$ с двумя арифметическими операциями — сложением и умножением. RSA применяет мультипликативную группу $G = < {Z_n}^*, \times >$ для генерации ключей.
Никаких разрушительных атак на RSA не было обнаружено. Теоретически предсказано несколько атак, основанных на разложении на множители, выборке шифрованного текста, образце дешифрования, образце шифрования, исходном тексте, модуле и реализации.
Криптосистема Рабина — вариант криптографической системы RSА. RSA базируется на экспоненциальном сравнении; криптосистема Рабина базируется на квадратичном сравнении. Мы можем представлять себе, что криптосистема Рабина — это RSA, в которой значение e = 2 и d = 1/2. Криптографическая система Рабина безопасна, пока p и q — большие числа. Сложность криптосистемы Рабина — на том же самом уровне, как и процесс разложения большого числа n на два простых сомножителя p и q.
Криптосистема Эль-Гамаля базируется на проблеме дискретного логарифма. Криптосистема Эль-Гамаля использует идею первообразных корней в Z_n^*. Шифрование и дешифрование в криптосистеме Эль-Гамаля использует группу $G = < {Z_p}^*, \times >$ Общедоступный ключ — это два числа, e₁ и e₂, а секретный ключ — это целое число d. Безопасность криптосистемы Эль-Гамаля основана на том, что решение проблемы дискретного логарифма не существует. Однако в литературе была упомянута атака, основанная на малом значении модуля, и атака знания исходного текста.
Другая криптографическая система, рассмотренная в этой лекции, базируется на эллиптических кривых. Эллиптические кривые являются кубическими уравнениями в двух переменных. Эллиптические кривые на поле вещественных чисел используют специальный класс эллиптических кривых y² = x³ + ax + b, где $4{a^3} + 27{b^2} \ne 0$ . Абелева группа была определена с помощью эллиптической кривой с операцией сложения, которая показывает, как две точки на кривой можно сложить, чтобы получить другую точку на этой кривой.
Криптография эллиптической кривой применяет две алгебраических структуры, абелеву группу и поле. Поле может быть полем вещественных чисел, GF (p) и GF (2ⁿ). Мы показали, как криптосистема Эль-Гамаля может моделироваться, используя эллиптические кривые в конечном поле. Безопасность криптографии эллиптической кривой зависит от проблемы логарифма эллиптической кривой, решение которой неосуществимо при большом значении модуля.

15.6. Набор для практики

Обзорные вопросы

Найдите различия между криптосистемами с симметричными ключами и асимметричными ключами.
Найдите различия между открытыми и секретными ключами в криптосистеме с асимметричными ключами. Найдите совпадения и различие ключей в криптосистемах с симметричными ключами и с асимметричными ключами.
Определите "лазейку" в односторонней функции и объясните её использование в криптографии с асимметричным ключом.
Кратко объясните идею ранцевой криптосистемы
- Что является односторонней функцией в этой системе?
- Что является лазейкой в этой системе?
- Определите открытые и секретные ключи в этой системе.
- Опишите безопасность этой системы.
Кратко объясните идею криптографической системы RSA.
- Что является односторонней функцией в этой системе?
- Что является лазейкой в этой системе?
- Определите открытые и секретные ключи в этой системе.
- Опишите безопасность этой системы.
Кратко объясните идею криптосистемы Рабина.
- Что является односторонней функцией в этой системе?
- Что является лазейкой в этой системе?
- Определите открытые и секретные ключи в этой системе.
- Опишите безопасность этой системы.
Кратко объясните идею криптосистемы Эль-Гамаля.
- Что является односторонней функцией в этой системе?
- Что является лазейкой в этой системе?
- Определите открытые и секретные ключи в этой системе.
- Опишите безопасность этой системы.
Кратко объясните идею криптографии эллиптической кривой (ECC).
- Что является односторонней функцией в этой системе?
- Что является лазейкой в этой системе?
- Определите открытые и секретные ключи в этой системе.
- Опишите безопасность этой системы.
Определите эллиптические кривые и объясните их приложения в криптографии.
Определите операцию, используемую в абелевой группе, которая обрабатывает точки на эллиптической кривой.

Упражнения

Учитывая сверхвозрастающий кортеж b = [7, 11,23,43,87, 173, 357], r =41 и модуль n = 1001, зашифруйте и расшифруйте букву a, используя ранцевую криптосистему. Используйте [7 6 5 1 2 3 4] как таблицу перестановки.
В RSA:
- Дано n = 221 и e = 5, найдите d.
- Дано n =3937 и e =17, найдите d.
- Дано p = 19, q = 23 и e = 3, найдите n, $\varphi ,$ (n) (^) и d.
Для того чтобы понять безопасность алгоритма RSА, найдите d, если вы знаете, что e =17, а n =187.
В RSA дано n и $\varphi (n)$ , вычислите p и q.
В RSA дано e = 13 и n = 100. Зашифруйте сообщение "HOW ARE YOU", применяя 00 к 25 для букв от A до Z и 26 — для пробела. Используйте различные блоки, чтобы сделать P <n.
В RSA дано n = 12091 и e = 13. Зашифруйте сообщение "THIS IS THOGH", используя схему кодирования 00 к 26. Расшифровать зашифрованный текст, чтобы найти первоначальное сообщение.
В RSA:
- Почему Боб не может выбрать 1 как открытый ключ e?
- Какова проблема в выборе 2 открытым ключом?
Алиса использует открытый ключ RSА Боба (e = 17, n = 19519), чтобы передать сообщение из четырех символов Бобу, применяющему схему 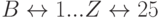$A \leftrightarrow 0$ , $B \leftrightarrow 1...Z \leftrightarrow 25$ кодирования и декодирования по каждому символу отдельно. Ева перехватывает зашифрованный текст (6625 0 2968 17863) и расшифровывает сообщение, не разлагая на множители модуль. Найдите исходный текст; объясните, почему Ева смогла легко взломать зашифрованный текст.
Алиса использует открытый ключ RSА Боба (e = 7, n = 143), чтобы передать исходный текст P = 8, зашифрованный в виде текста C = 57. Покажите, как Ева может использовать атаку выборки текста, если она имеет доступ к компьютеру Боба, чтобы найти исходный текст.
Алиса использует общедоступный ключ RSA Боба (e = 3, n = 35) и передает зашифрованный текст 22 Бобу. Покажите, как Ева может найти исходный текст, используя атаку циклического повторения.
Предложите, как Алиса может предотвратить атаку связанного сообщения на RSA.
Используя криптосистему Рабина с p = 47 и q =11:
- Зашифруйте P = 17 и найдите зашифрованный текст.
- Используя Китайскую теорему об остатках, найдите четыре возможных исходных текста.
В криптосистеме Эль-Гамаля дано простое число p = 31:
- Выберите соответствующие e₁ и d, затем вычислите e₂.
- Зашифруйте сообщение "HELLO" ; используйте 00 к 25 для кодирования. Используйте различные блоки для того, чтобы сделать P<p.
- Расшифруйте зашифрованный текст, чтобы получить исходный текст.
Что случится в криптосистеме Эль-Гамаля —, если C₁ и C₂ будут изменены в течение передачи?
Предположим, что Алиса применяет в криптосистеме Эль-Гамаля общедоступный ключ Боба ( e₁ = 2 и e₂ = 8 ), чтобы передать два сообщения — P = 17 и P' = 37. Они оба используют то же самое случайное целое число r = 9. Ева перехватывает зашифрованный текст и так или иначе находит значение P = 17. Покажите, как Ева может использовать атаку знания исходного текста, чтобы найти значение P'.
В эллиптической кривой E (1, 2) в поле GF (11):
- Найдите уравнение кривой.
- Найдите все точки на кривой и сделайте рисунок, такой же, как рис. 15.5.
- Сгенерируйте общедоступный и секретный ключи для Боба.
- Выберите точку на кривой как исходный текст Алисы.
- Создайте зашифрованный текст, соответствующий исходному тексту Алисы в пункте d.
- Расшифруйте зашифрованный текст для Боба, чтобы найти исходный текст, передаваемый Алисой.
В эллиптической кривой E (g⁴, 1) в поле GF(2⁴):
- Найдите уравнение кривой.
- Найдите все точки на кривой и сделайте рисунок, такой же, как рис. 15.5.
- Сгенерируйте общедоступный и секретный ключи для Боба.
- Выберите точку на кривой как исходный текст Алисы.
- Создайте зашифрованный текст, соответствующий исходному тексту Алисы в пункте г.
- Расшифруйте зашифрованный текст для Боба, чтобы найти исходный текст, передаемый Алисе.
Используйте ранцевую криптосистему:
- Напишите алгоритм для шифрования.
- Напишите алгоритм для дешифрования.
В RSA:
- Напишите алгоритм для шифрования, используя оптимальное асимметричное дополнение шифрования (OAEC).
- Напишите алгоритм для дешифрования, используя оптимальное асимметричное дополнение шифрования (OAEC).
Напишите алгоритм для атаки циклического повторения на RSA.
Напишите алгоритм для сложения двух точек на эллиптической кривой в GF(p).
Напишите алгоритм для сложения двух точек на эллиптической кривой в GF(2ⁿ).