Рационализация переборных алгоритмов

Теорема 5. В хордальном графе всякое минимальное разделяющее множество является кликой.

Доказательство. Допустим, что в некотором графе есть минимальное разделяющее множество , не являющееся кликой. Это означает, что в имеются несмежные вершины и . При удалении множества образуется не менее двух новых компонент связности. Пусть 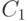и 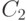- такие компоненты. Вершина смежна, по крайней мере, с одной вершиной в каждой из этих компонент. Действительно, если была бы не смежна, скажем, ни с одной из вершин компоненты 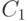, то множество тоже было бы разделяющим, а это противоречит минимальности разделяющего множества . То же относится к вершине . 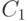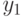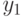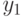Выберем в компоненте такие вершины и , чтобы была смежна с вершиной , - с вершиной и при этом расстояние между и в 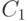было минимальным (возможно ). Аналогично выберем и 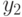в компоненте 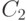. 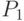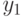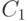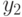Пусть - кратчайший путь из в в компоненте , а - кратчайший путь из в в компоненте 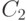(каждый из этих путей может состоять из одной вершины). Тогда последовательность является простым циклом без хорд длины не менее 4. Следовательно, граф - не хордальный.

Теорема 6. В любом хордальном графе имеется симплициальная вершина.

Доказательство. В полном графе любая вершина является симплициальной. Докажем индукцией по числу вершин , что в любом хордальном графе, не являющемся полным, есть две несмежные симплициальные вершины. При 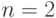это, очевидно, так. Пусть - хордальный граф с вершинами, 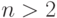, не являющийся полным. Если несвязен, то, по предположению индукции, во всех компонентах связности есть симплициальные вершины. Допустим, что граф связен. Так как он не полный, то в нем есть разделяющее множество, а по теореме 5 есть разделяющая клика. Пусть - такая клика, и - две новые компоненты связности, появляющиеся при удалении из графа всех вершин клики . Рассмотрим подграф , порожденный множеством 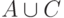. Если он полный, то в нем любая вершина симплициальна. Если же он не полный, то по предположению индукции в нем есть две несмежные симплициальные вершины. Хотя бы одна из этих двух вершин принадлежит множеству . Итак, в любом случае в множестве имеется вершина , являющаяся симплициальной в графе . Окрестность вершины во всем графе совпадает с ее окрестностью в подграфе . Следовательно, - симплициальная вершина графа . Аналогично, в множестве имеется симплициальная вершина графа и она не смежна с вершиной .

Теорема 7. Для любого хордального графа .

Доказательство. Пусть - хордальный граф с вершинами и . Покажем, что граф можно правильно раскрасить в цветов. Найдем в нем симплициальную вершину и обозначим ее через 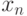, а граф, полученный удалением этой вершины, через 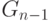. Этот граф тоже хордальный, значит, в нем тоже есть симплициальная вершина. Пусть 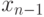- симплициальная вершина в графе 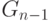, а - граф, получаемый из него удалением этой вершины. Продолжая действовать таким образом, получим последовательность вершин и последовательность графов (здесь ), причем при каждом вершина является симплициальной в графе 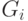, а граф получается из 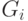удалением этой вершины.

Допустим, что граф правильно раскрашен в цветов. Покажем, что вершину можно покрасить в один из этих цветов, сохраняя правильность раскраски. Действительно, - симплициальная вершина графа 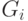, значит, множество всех смежных с ней в этом графе вершин является кликой. Так как при добавлении к множеству вершины тоже получается клика, а мощность наибольшей клики в графе равна , то . Значит, для окрашивания вершин множества использовано не более цвета. Поэтому для вершины можно использовать один из оставшихся цветов.

Итак, каждый из графов 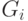, а значит, и исходный граф , можно правильно раскрасить в цветов. Отсюда следует, что . Обратное неравенство было установлено в "Раскраски" .