| Здравствуйте. Как оформить документы для получения диплома по курсу повышения квалификации? |
Алгоритмы вычисления размерностных многочленов
13.4. ЛЕММА. Пусть  является
является 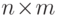 -матрицей
-матрицей 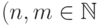 ;
;  ,
, 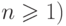 , состоящей из
нулей и единиц. Если первый столбец матрицы
, состоящей из
нулей и единиц. Если первый столбец матрицы  состоит только из
нулей,
а матрица
состоит только из
нулей,
а матрица  получена из
получена из  удалением этого нулевого
столбца, то
удалением этого нулевого
столбца, то 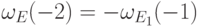 .
.
ДОКАЗАТЕЛЬСТВО.
Применяя формулу (12.2) к матрице  и вектору
и вектору 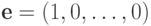 , получим
, получим 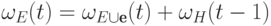 , где
, где  -
матрица с элементами
-
матрица с элементами  (
( 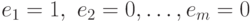 суть
координаты вектора
суть
координаты вектора  ). Очевидно,
). Очевидно,  и
и 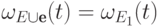 (см. теорему 12.8(8)), так что
(см. теорему 12.8(8)), так что  и, в частности,
и, в частности,  . Поскольку
. Поскольку  содержит нулевой
столбец, из леммы
13.3(2) следует, что
содержит нулевой
столбец, из леммы
13.3(2) следует, что 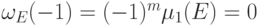 , значит,
, значит, 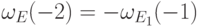 .
.
13.5. ЛЕММА. Пусть 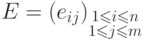
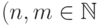 ;
;  ,
, 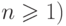 является
является 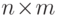 -матрицей состоящей из
нулей и единиц. Предположим, что
-матрицей состоящей из
нулей и единиц. Предположим, что  для
для 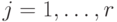 и
и  для
для 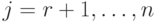
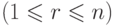 . Тогда
. Тогда 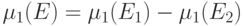 , где
матрица
, где
матрица  получена
из
получена
из  удалением первого столбца, а
удалением первого столбца, а  получена из
получена из  удалением
удалением  первых строк.
первых строк.
ДОКАЗАТЕЛЬСТВО.
Применяя (12.2) к  и
и 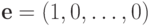 ,
получаем
,
получаем 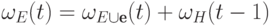 , где
, где  -
- 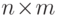 -матрица с элементами
-матрица с элементами
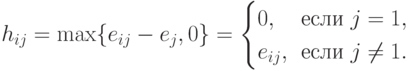
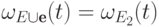 , следовательно,
, следовательно,  . Далее, пользуясь леммой 13.4, можно написать
. Далее, пользуясь леммой 13.4, можно написать 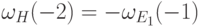 , значит,
, значит,  . Теперь, по лемме 13.2 имеем
. Теперь, по лемме 13.2 имеем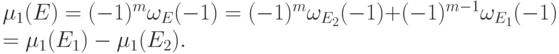
13.6. СЛЕДСТВИЕ. Пусть
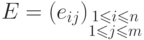
 -
- 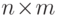 -матрица, состоящая из 0 и 1. Предположим, что
существуют
-матрица, состоящая из 0 и 1. Предположим, что
существуют  , такие, что
, такие, что 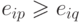 для всех
для всех 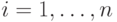 . Тогда
. Тогда 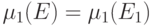 , где
, где  получена из
получена из  удалением
удалением  -го столбца.
-го столбца.
ДОКАЗАТЕЛЬСТВО.
Поскольку размерностный многочлен матрицы  инвариантен
относительно перестановок строк
(или столбцов) матрицы
инвариантен
относительно перестановок строк
(или столбцов) матрицы  , значение
, значение 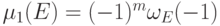 также обладает этим свойством.
Поэтому, без потери общности, можно считать, что
также обладает этим свойством.
Поэтому, без потери общности, можно считать, что 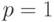 и существует
и существует  , такое, что
, такое, что 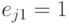 для
для 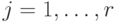 ,
и
,
и 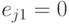 для
для 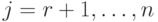 . По лемме 13.5,
. По лемме 13.5, 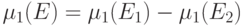 , где
, где  получена из
получена из  удалением первого столбца и
удалением первого столбца и  первых строк (поскольку
первых строк (поскольку  для
для  , каждый элемент
, каждый элемент  -го столбца матрицы
-го столбца матрицы  равен нулю).
Следовательно,
равен нулю).
Следовательно, 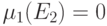 (см. лемму 13.3(2)), так что
(см. лемму 13.3(2)), так что  .
.
13.7. ЛЕММА. Пусть
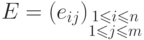
 -
- 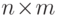 -матрица, состоящая из 0 и 1. Предположим, чт о
-матрица, состоящая из 0 и 1. Предположим, чт о  содержит строку
содержит строку 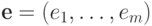 , такую, что
, такую, что 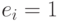 для
для 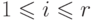 и
и  для
для 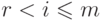
 . Тогда
. Тогда 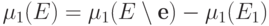 , где матрица
, где матрица 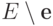 получена удалением строки
получена удалением строки  из матрицы
из матрицы  , а
, а  - матрица
- матрица  получена из матрицы
получена из матрицы 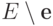 удалением
удалением  первых столбцов.
первых столбцов.
ДОКАЗАТЕЛЬСТВО.
Применяя формулу (12.3) к матрице  и строке
и строке 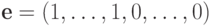 , получаем
, получаем  , где матрица
, где матрица  получена из
получена из  присоединением слева
присоединением слева  нулевых столбцов.
Теперь из (12.2) видно, что
нулевых столбцов.
Теперь из (12.2) видно, что 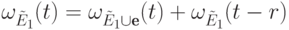 ,
следовательно,
,
следовательно,

Поскольку  содержит нулевой столбец, из пункта 2
леммы 13.3 следует, что
содержит нулевой столбец, из пункта 2
леммы 13.3 следует, что 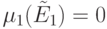 , значит,
, значит,
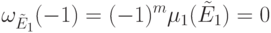
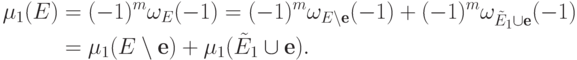
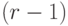 столбцов матрицы
столбцов матрицы 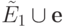 мажорирует
мажорирует  -й столбец этой матрицы, из следствия 13.6 вытекает, что
-й столбец этой матрицы, из следствия 13.6 вытекает, что  , где
, где  - матрица, полученная присоединением слева
нулевого столбца к
- матрица, полученная присоединением слева
нулевого столбца к  . Применяя теперь п.5 леммы
13.3,
получаем
. Применяя теперь п.5 леммы
13.3,
получаем 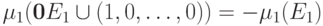 ,
откуда следует требуемое
соотношение
,
откуда следует требуемое
соотношение  .
.Пусть
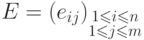 -
- 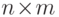 -матрица. По теореме 12.8
п.5, удаление "лишних" строк матрицы
-матрица. По теореме 12.8
п.5, удаление "лишних" строк матрицы  не меняет
размерностный многочлен этой матрицы, значит, не меняет и
значение
не меняет
размерностный многочлен этой матрицы, значит, не меняет и
значение 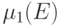 . Кроме того, если любой элемент
матрицы
. Кроме того, если любой элемент
матрицы  равен либо 0, либо
1, то из следствия 13.6 вытекает,
что удаление "лишних" столбцов матрицы
равен либо 0, либо
1, то из следствия 13.6 вытекает,
что удаление "лишних" столбцов матрицы  не меняет
значения
не меняет
значения 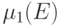 (
(  -й столбец матрицы
-й столбец матрицы 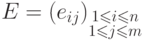
 называется "лишним", если существует число
называется "лишним", если существует число 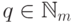 ,
такое, что
,
такое, что 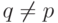 и
и 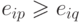 для
всех
для
всех 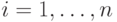 ).
).
Таким образом, в ходе
вычисления 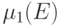 (где
(где  -
- 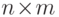 -матрица, состоящая из 0 и 1) мы можем прежде всего отбросить "лишние"
строки и столбцы (по п.5 леммы 13.3, эти вычисления сопровождаются соответствующими
изменениями знака
-матрица, состоящая из 0 и 1) мы можем прежде всего отбросить "лишние"
строки и столбцы (по п.5 леммы 13.3, эти вычисления сопровождаются соответствующими
изменениями знака 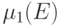 ), а затем отбросить строки и столбцы,
удовлетворяющие соотношениям леммы
13.5. Затем мы можем выбрать одну из
следующих альтернатив:
воспользоваться леммой 13.5 для
вычисления
), а затем отбросить строки и столбцы,
удовлетворяющие соотношениям леммы
13.5. Затем мы можем выбрать одну из
следующих альтернатив:
воспользоваться леммой 13.5 для
вычисления 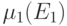 (где
(где  - матрица,
полученная из
- матрица,
полученная из  с помощью описанного выше процесса сокращения) или
вычислить
с помощью описанного выше процесса сокращения) или
вычислить 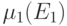 , воспользовавшись
леммой 13.7, т. е.
"раскладывая"
, воспользовавшись
леммой 13.7, т. е.
"раскладывая"  по строкам и столбцам соответственно.
Очевидно, что если число строк матрицы
по строкам и столбцам соответственно.
Очевидно, что если число строк матрицы  больше числа ее
столбцов, то предпочтительнее
"движение по столбцам" с помощью леммы 13.5, в противном случае для
вычисления
больше числа ее
столбцов, то предпочтительнее
"движение по столбцам" с помощью леммы 13.5, в противном случае для
вычисления 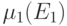 целесообразно воспользоваться леммой 13.7.
целесообразно воспользоваться леммой 13.7.
