| Непонятен ход решения задачи |
Excel для математиков
Задача 12 Решение системы линейных уравнений и обращение матриц
Постановка задачи: Найти решение системы линейных уравнений AX = B
Чтобы одним выстрелом "убить двух зайцев", рассмотрим эту задачу в более общей постановке. Будем полагать, что B - это не вектор правых частей, а матрица из m столбцов, каждый из которых задает правую часть уравнения. Тем самым мы будем решать m систем линейных уравнений с одной и той же левой частью и разными правыми частями. Переход от решения одной системы уравнений к решению m систем сам по себе является важным достоинством рассматриваемого алгоритма. Но более важно то, что здесь же становится возможным находить обратную матрицу для A. Достаточно задать в качестве матрицы правых частей B единичную матрицу E, и тогда матрица X будет обратной к A.
Заголовок функции, решающей эту задачу, имеет такой же вид, как и при умножении матриц и отличается только именем функции:
Function SLEQ(A As Variant, B As Variant) As Variant
Эта функция имеет два входных параметра, - матрицу коэффициентов системы уравнений и матрицу правых частей, и возвращает как результат матрицу X. Конечно, реализация этой функции требует больших усилий, чем умножение матриц. Мне пришлось написать пять процедур, вызываемых в процессе вычислений функции SLEQ. Но сама идея алгоритма достаточно прозрачна. Вначале строится расширенная матрица AB путем присоединения справа матрицы B к матрице A. Затем линейными преобразованиями над ее строками матрица A переводится в единичную матрицу E. Эти же преобразования переводят матрицу B в решение X. Если в качестве B задать единичную матрицу, X будет представлять обратную матрицу. Если B - вектор из одного столбца, то речь идет об обычной системе линейных уравнений. В промежуточном случае B представляет прямоугольную матрицу, и тогда одновременно получа R± ется решение для m систем линейных уравнений. Теперь приведу текст функции SLEQ и прокомментирую его, а затем уже приведу процедуры, вызываемые по ходу работы. Вот текст основной функции, вызываемой в формуле над массивами рабочего листа Excel:
Public Function SLEQ(A As Variant, B As Variant) As Variant 'Решение системы линейных уравнений: AX = B 'A - матрица коэффициентов, B - матрица правых частей. 'X - матрица решений. 'Для каждого столбца B1 матрицы B соответствующий столбец X1 'является решением системы AX1 = B1. 'Если B - единичная матрица E, то X - матрица, обратная к A. Dim i As Integer, j As Integer Dim N As Integer, M As Integer Dim msg1 As String, msg2 As String msg1 = " При вызове SLEQ система уравнений линейно зависима!" msg2 = " При вызове SLEQ некорректно задана размерность системы уравнений!" 'Проверка корректности задания размерности СЛУР. N = A.Rows.Count If (A.Columns.Count = N) And (B.Rows.Count = N) Then 'Размерность задана корректно. M = B.Columns.Count ReDim AB(1 To N, 1 To N + M) 'Построение расширенной матрицы. For i = 1 To N For j = 1 To N AB(i, j) = A.Cells(i, j) Next j Next i For i = 1 To N For j = 1 To M AB(i, N + j) = B.Cells(i, j) Next j Next i 'Цикл линейных преобразований над матрицей AB. Dim k As Integer Dim Independence As Boolean k = 1: Independence = True Do Independence = FindMax(AB, k, i) If Not Independence Then Exit Do Call Change(AB, k, i) Call Normalization(AB, k) Call Linear(AB, k) k = k + 1 Loop While k <= N If Not Independence Then MsgBox (msg1) 'Возвращение результата. For i = 1 To N For j = 1 To M AB(i, j) = AB(i, j + N) Next j Next i ReDim Preserve AB(1 To N, 1 To M) SLEQ = AB Else 'Некорректно задана размерность. MsgBox (msg2) End If End Function
Дам теперь необходимые пояснения:
- В реализации функции можно выделить три основные части: построение расширенной матрицы, цикл линейных преобразований и формирование результирующей матрицы. Для построения расширенной матрицы вводится динамический массив AB. Его заполнение достаточно очевидно. Окончательный результат представляет лишь часть расширенной матрицы и формируется на месте исходной матрицы B. Чтобы выделить эту часть, я использую возможности динамического массива: переопределяю его размерность и затем, используя спецификатор Preserve, сохраняю нужные результаты. Таким образом, новый массив не вводится, а сжимается существующий до нужного размера. Правда, это сжатие возможно лишь для последнего измерения. Поэтому предварительно нужные результаты переписываются в начало массива AB.
- С содержательной точки зрения основу алгоритма составляет цикл, в котором над матрицей выполняются линейные преобразования. Алгоритм реализует схему Гаусса с выбором главного элемента в столбце. На каждом шаге цикла линейными преобразованиями над строками матрицы ее очередной k -й столбец приводится к единичному столбцу с единицей на диагонали матрицы и остальными нулевыми элементами. Вначале вызывается функция FindMax, которая в k -ом столбце находит максимальный по модулю элемент, расположенный ниже диагонали. Процедура Change меняет строки местами, так чтобы найденный максимальный элемент стал диагональным. Процедура Normalization нормирует k -ю строку делением всех ее элементов на элемент, расположенный на диагонали. Сам этот элемент тем самым становится равным 1. Процедура Linear выполняет линейные преобразования над строками, вычитая из каждой строки k -ю строку, умноженную на подходящий коэффициент, так чтобы сделать нулевыми все элементы k -го столбца, расположенные выше и ниже диагонали.
- Вначале проверяется корректность задания размерности матриц A и B. Подобная проверка проводилась при умножении матриц. Вторая проверка позволяет обнаружить линейную зависимость строк или столбцов матрицы A. В случае линейной зависимости система уравнений не имеет единственного решения, а обратную матрицу вычислить невозможно.
- Данная функция является чисто пользовательской, и я ориентируюсь лишь на один способ передачи параметров, - в виде Range -объектов.
Приведу теперь тексты процедур, вызываемых в теле функции SLEQ, и начну с функции FindMax:
Public Function FindMax(A() As Variant, ByVal Num As Integer, _ Ind As Integer) As Boolean 'В столбце с номером Num матрицы A, начиная с диагонального элемента, 'ищется максимальный по абсолютной величине элемент, 'и вычисляется его индекс Ind. 'Функция возвращает true, если элемент отличен от нуля. Dim i As Integer, Elem As Variant Elem = Abs(A(Num, Num)): Ind = Num For i = Num + 1 To UBound(A, 1) If Abs(A(i, Num)) > Elem Then Elem = Abs(A(i, Num)): Ind = i End If Next i FindMax = Not (Elem = 0) End Function
Прежде всего, заметьте, что в теле пользовательской функции SLEQ вызываются обычные процедуры и функции. Помимо своей основной задачи - нахождения максимального по модулю элемента столбца и определения его индекса Ind, -булева функция FindMax позволяет определить, является ли система уравнений линейно зависимой. Если найденный элемент равен 0, то и все остальные элементы равны 0, а это и есть признак линейной зависимости. Эта проверка предохраняет нас от возможного деления на 0. Конечно, разумнее выполнять не строгую, а слабую проверку на 0, полагая, что система "почти линейно зависима" (плохо обусловлена), если вычисляемый нами элемент близок к 0. Но это уже вычислительные, а не программистские аспекты, которые здесь обсуждать не место. Следующие две процедуры Change и Normalization совсем простые:
Public Sub Change(A() As Variant, _ ByVal Ind1 As Integer, ByVal Ind2 As Integer) 'Перестановка строк с индексами Ind1 и Ind2 матрицы A Dim i As Integer, Elem As Variant If Not (Ind1 = Ind2) Then For i = LBound(A, 2) To UBound(A, 2) Elem = A(Ind1, i) A(Ind1, i) = A(Ind2, i) A(Ind2, i) = Elem Next i End If End Sub Public Sub Normalization(A() As Variant, Ind As Integer) 'Нормировка строки с индексом Ind матрицы A 'делением на диагональный элемент. Dim i As Integer, Elem As Variant Elem = A(Ind, Ind): A(Ind, Ind) = 1 For i = Ind + 1 To UBound(A, 2) A(Ind, i) = A(Ind, i) / Elem Next i End Sub
Процедура Linear выполняет линейное преобразование над строками матрицы. Под линейным преобразованием понимается добавление к одной строке матрицы другой строки, умноженной на произвольный коэффициент. Вот текст этой процедуры:
Public Sub Linear(A() As Variant, Ind As Integer) 'Линейные преобразования над строками матрицы A. 'В результате столбец Ind становится единичным. Dim i As Integer For i = 1 To Ind - 1 Call AddLine(A, Ind, i) Next i For i = Ind + 1 To UBound(A, 1) Call AddLine(A, Ind, i) Next i End Sub
В процедуре Linear поочередно изменяются все строки за исключением строки с номером Ind. Целью линейных преобразований является получение нулей выше и ниже диагонали в столбце с заданным индексом Ind. Для этого в теле Linear организованы два цикла, в которых вызывается процедура AddLine, выполняющая линейное преобразование для заданной строки.
Public Sub AddLine(A() As Variant, _ ByVal Ind1 As Integer, ByVal Ind2 As Integer) 'Cтрока с индексом Ind1 с соответствующим коэффициентом 'вычитается из строки Ind2 матрицы A Dim i As Integer, Elem As Variant Elem = A(Ind2, Ind1) For i = Ind1 To UBound(A, 2) A(Ind2, i) = A(Ind2, i) - A(Ind1, i) * Elem Next i End Sub
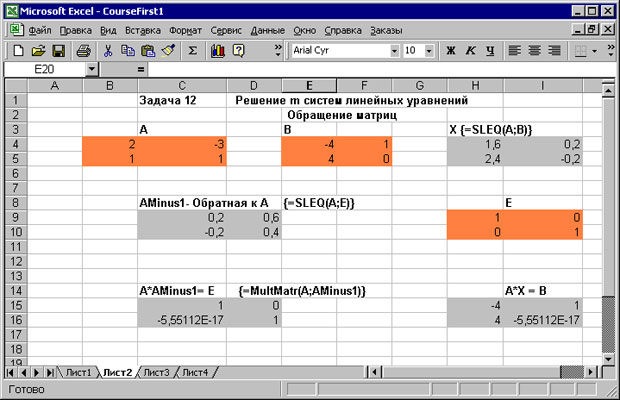
Нам остается привести результаты тестирования функции SLEQ. Вот как они выглядят на рабочем листе Excel:
В ячейки рабочего листа я ввел матрицу A, матрицу правых частей B и единичную матрицу E, дав всем этим массивам соответствующие имена. Матрица B состоит из двух столбцов, так что, вызвав функцию SLEQ в формуле над массивами - {=SLEQ(A;B)}, я "одним махом" решил две системы линейных уравнений, получив решение в матрице X, каждый столбец которой является решением соответствующей системы уравнений. Затем, используя в формуле над массивами единичную матрицу E - {=SLEQ(A; E)}, я вычислил матрицу, обратную к A. Для проверки качества решения я, используя вызов MultMatr, умножил матрицу A на полученную обратную матрицу AMinus1, а также A умножил на X. В первом случае получена "почти" единичная матрица (один из элементов не равен точно 0 ), во втором случае результат умножения, как и дол жно, практически совпадает с матрицей B.