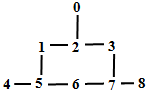| Выполнение каких функций не изменяет позицию указателя в файле? |
Решение задач на использование алгоритмов обработки данных
Алгоритмы на графах
Многие прикладные задачи и задачи повышенной сложности легко сформулировать в терминах такой структуры данных как граф. Для ряда подобных задач хорошо изучены эффективные (полиномиальные) алгоритмы их решения.
Для хранения графа в программе можно применить различные методы. Самым простым является хранение матрицы смежности, с помощью которой легко проверить, существует ли в графе ребро, соединяющее вершину одну с вершиной с другой. Основной же ее недостаток заключается в том, что матрица смежности требует, чтобы объем памяти был достаточен для хранения N2 значений, даже если ребер в графе существенно меньше, чем N2. Это не позволяет построить алгоритм со временем порядка O(N) для графов, имеющих O(N) ребер.
Данного недостатка лишены такие способы хранения графа, как одномерный массив длины N списков или множеств вершин. В таком массиве каждый элемент соответствует одной из вершин и содержит список или множество вершин, смежных ей.
Для реализации некоторых алгоритмов более удобным является описание графа путем перечисления его ребер. В этом случае хранить его можно в одномерном массиве длиной M, каждый элемент которого содержит запись о номерах начальной и конечной вершин ребра, а также его весе в случае взвешенного графа.
При решении многих задач, как для ориентированных, так и для неориентированных графов, необходим эффективный метод систематического обхода вершин графа. На практике применяется два принципиально различных порядка обхода, основанных на поиске в глубину и поиске в ширину соответственно.
Для определения и нахождения длины кратчайшего пути в графе в основном используют известные алгоритмы, такие как алгоритм Дейкстры, Флойда и переборные алгоритмы.
Графы широко используются в различных областях науки и техники для моделирования отношений между объектами. Объекты соответствуют вершинам графа, а ребра – отношениям между объектами.
Пример 2. Задача "Тетраэдр"
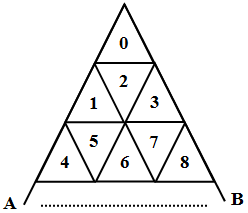
Дано треугольное поле в виде равностороннего треугольника. Оно разбито на одинаковые равносторонние треугольники со сторонами в М раз меньшими, чем сторона большого треугольника ( рис. 46.1).
Маленькие треугольники пронумерованы подряд с верхнего ряда вниз по рядам, начиная с 0. Числами показаны номера треугольников. I -му треугольнику приписана пометка Pi.
Имеется также тетраэдр (правильная треугольная пирамида) с ребром, равным длине стороны маленького треугольника. Тетраэдр установлен на S -м треугольнике. Все грани тетраэдра пронумерованы следующим образом:
- основание тетраэдра;
- правая грань тетраэдра, если смотреть сверху тетраэдра в направлении стороны АВ перпендикулярно ей;
- левая грань тетраэдра, если смотреть сверху тетраэдра в направлении стороны АВ перпендикулярно ей;
- оставшаяся грань.
Например, при S=2 жирной линией выделено нижнее ребро третьей грани, а при S=3 жирной линией выделено нижнее ребро второй грани. J -я грань тетраэдра имеет пометку Rj.
Имеется возможность перекатывать тетраэдр через ребро, но при каждом перекатывании взимается штраф, равный квадрату разности между пометками совмещаемой грани тетраэдра и треугольника. Требуется перекатить тетраэдр с треугольника S на D с наименьшим суммарным штрафом  .
.
Входные данные находятся в текстовом файле INPUT.TXT. Первая строка содержит целые числа S, D и М (M<=90). Каждая из следующих M2 строк содержит пометку соответствующего треугольника. В последней строке записаны пометки граней тетраэдра. Пометки (как граней, так и треугольников) – целые неотрицательные числа, не превосходящие 300. Числа в одной строке разделены пробелами.
В выходной файл OUTPUT.TXT должно быть записано одно число – минимально возможный штраф.
Пример.
Описание решения.
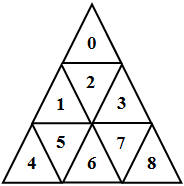
Перейдем к графу следующим образом: вершина – маленький треугольник. Ребро – наличие возможности перекатить тетраэдр через ребро из одного треугольника в другой. Тогда, например, поле, изображенное на рис. 46.2, превратится в граф на рис. 46.3.
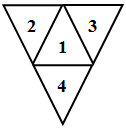
На этом графе требуется найти путь минимальной стоимости из одной вершины в другую. Поскольку веса ребер в этом графе зависят от того, какой именно гранью тетраэдр придет на соответствующий треугольник, то воспользуемся поиском в ширину. Но прежде проясним процесс перекатывания тетраэдра. В соответствии с условиями задачи начальное положение развертки тетраэдра показано на рис. 46.4.
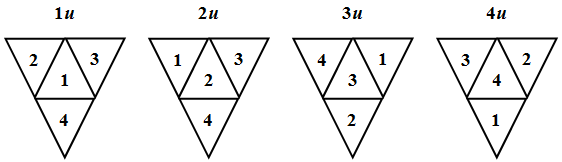
Обозначим его 1u (в основании грань номер 1, повернутая вверх). Очевидно, что всего существует 8 возможных различных состояний тетраэдра: 1u, 2u, Зu, 4u, 1d, 2d, 3d, 4d. На рис. 46.5 и рис. 46.6 приведены соответствующие развертки:
Составим теперь таблицу, отображающую, в какое из состояний переходит тетраэдр при перекатывании его вниз, вверх, вправо, влево из текущего состояния.
| Вниз | Вверх | Вправо | Влево | |
| 1u | 4d | x | 3d | 2d |
| 1d | x | 4u | 2u | 3u |
| 2u | 3d | x | 4d | 1d |
| 2d | x | 3u | 1u | 4u |
| 3u | 2d | x | 1d | 4d |
| 3d | x | 2u | 4u | 1u |
| 4u | 1d | x | 2d | 3d |
| 4d | x | 1u | 3u | 2u |
Для удобства использования этой информации введем следующее кодирование:
Получаем двумерный массив Т (8 строк, 4 столбца), который описывает все возможные перекатывания тетраэдра.
Основная идея решения заключается в следующем:
- заносим в очередь стартовую позицию S ;
- пока очередь не пуста, берем из очереди очередную позицию, ставим в очередь позиции, в которые тетраэдр может попасть за одно перекатывание.
При установке в очередь очередной элемент включает номер вершины на графе, тип прихода (1u...4d), текущий штраф после перехода в эту вершину. Элемент не нужно ставить в очередь, если текущий штраф больше ранее запомненного для этой вершины графа.
#include "stdafx.h"
#include <iostream>
#include <cmath>
using namespace std;
void InputData();
void OutResult();
void InitGraph();
void Put(long long v, long long tv, long long cv);
void Get(long long *v, long long *tv, long long *cv);
void PutAll(long long v, long long tv, long long cv);
long long SQR(long long a);
int MaxM = 10;
int Table[8][4] = {
8, 0, 6, 4,
0, 7, 3, 5,
6, 0, 8, 2,
0, 5, 1, 7,
4, 0, 2, 8,
0, 3, 7, 1,
2, 0, 4, 6,
0, 1, 5, 3
};
int MaxQ = MaxM * MaxM * MaxM;
int *p, *cp, *Pw, **g, **Q;
long long *R;
long long i, S, D, M, j, a, TS, QBegin, QEnd, V, TV, CV, Last;
//V – номер вершины
//TV – тип вершины
//CV – текущее значение штрафа
int _tmain(int argc, _TCHAR* argv[]){
p = new int[MaxM * MaxM];
cp = new int[MaxM * MaxM];
Pw = new int[MaxM * MaxM];
for (i = 0; i < MaxM * MaxM; i++)
p[i] = cp[i] = Pw[i] = 0;
g = new int*[MaxM * MaxM];
for (i = 0; i < MaxM * MaxM; i++ ){
g[i] = new int[4];
g[i][0] = g[i][1] = g[i][2] = g[i][3] = 0;
}
Q = new int*[MaxQ + 1];
for (i = 0; i < MaxQ + 1; i++ ){
Q[i] = new int[4];
Q[i][0] = Q[i][1] = Q[i][2] = Q[i][3] = Q[i][4] = 0;
}
R = new long long[5];
R[0] = R[1] = R[2] = R[3] = R[4] = 0;
InputData();
InitGraph();
QEnd = 0;
QBegin = 1;
Put(S,TS,0);
while (QBegin <= QEnd){
Get(&V,&TV,&CV);
PutAll(V,TV,CV);
}
OutResult();
system("pause");
return 0;
}
//описание функции ввода исходных данных
void InputData(){
FILE *f;
f = fopen("input.txt","r");
fscanf(f,"%d %d %d",&S,&D,&M);
for ( i = 0; i < M * M; i++ )
fscanf(f,"%d",p + i);
for ( i = 1; i < 5; i++ )
fscanf(f,"%d",R + i);
fclose(f);
}
//описание функции вывода результата
void OutResult(){
FILE *f;
f = fopen("output.txt","w");
fprintf(f,"%d",cp[D]);
fclose(f);
}
//описание функции создания графа по исходным данным
void InitGraph(){
Pw[0] = 1;
g[0][1] = 2;
for ( i = 1; i < M; i++)
for ( j = i * i; j < (i + 1) * (i + 1) - 1; j++){
g[j][++Pw[j]] = j + 1;
g[j + 1][++Pw[j + 1]] = j;
}
a = 4;
TS = 1;
for ( i = 1; i < M - 1; i++){
for ( j = i * i; j < (i + 1) * (i + 1); j += 2){
g[j][++Pw[j]] = j + a;
g[j + a][++Pw[j + a]] = j;
if ( S == j ) TS = 2;
}
a += 2;
}
for ( i = 0; i < M * M; i++)
cp[i] = INT_MAX;
}
//описание функции постановки в очередь одной вершины графа
void Put(long long v, long long tv, long long cv){
QEnd++;
Q[QEnd][1] = v;
Q[QEnd][2] = tv;
Q[QEnd][3] = cv;
cp[v] = cv;
}
//описание функции взятия из очереди очередной вершины графа
void Get(long long *v, long long *tv, long long *cv){
*v = Q[QBegin][1];
*tv = Q[QBegin][2];
*cv = Q[QBegin][3];
QBegin++;
}
/*описание функции постановки в очередь всех вершин, смежных с текущей*/
void PutAll(long long v, long long tv, long long cv){
long nv, ntv, ncv, Dir, Base;
for ( i = 1 ; i <= Pw[v]; i++ ){
nv = g[v][i];
if ( nv == v + 1 )
Dir = 2;
else if ( nv == v - 1 )
Dir = 3;
else if ( nv > v )
Dir = 0;
else Dir = 1;
ntv = Table[tv-1][Dir];
Base = (ntv + 1) / 2;
if ( Base > 0 ) {
ncv = cv + SQR(p[nv] - R[Base]);
if ( ncv < cp[nv] )
Put(nv,ntv,ncv);
}
}
}
//описание функции возведения в квадрат
long long SQR(long long a){
return a*a;
}
Листинг
.