| ВКР |
Статистика нечисловых данных
Теорема 2. Пусть  - топологическое пространство, непрерывная (в топологии произведения) функция
- топологическое пространство, непрерывная (в топологии произведения) функция 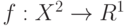 неотрицательна, симметрична (т.е.
неотрицательна, симметрична (т.е.  для любых
для любых  и
и  из
из  ), существует число
), существует число  такое, что при всех
такое, что при всех 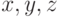 из
из 
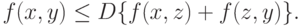 |
( 5) |
Пусть в  существует точка
существует точка  такая, что при любом положительном
такая, что при любом положительном  множество
множество 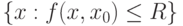 является бикомпактным. Пусть для случайного элемента
является бикомпактным. Пусть для случайного элемента 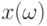 , согласованного с топологией в рассмотренном выше смысле, существует
, согласованного с топологией в рассмотренном выше смысле, существует 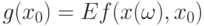 .
.
Тогда существуют (т.е. непусты) математическое ожидание 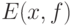 и эмпирические средние
и эмпирические средние 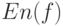 .
.
Замечание. Условие (5) - некоторое обобщение неравенства треугольника. Например, если  - метрика в
- метрика в  , а
, а 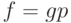 при некотором натуральном
при некотором натуральном  , то для
, то для  выполнено соотношение (5) с
выполнено соотношение (5) с  .
.
Доказательство. Рассмотрим функцию 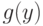 , определенную формулой (4). Имеем
, определенную формулой (4). Имеем
 |
( 6) |
Поскольку по условию теоремы 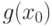 существует, а потому конечно, то из оценки (6) следует существование и конечность
существует, а потому конечно, то из оценки (6) следует существование и конечность 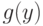 при всех
при всех  из
из  . Докажем непрерывность этой функции.
. Докажем непрерывность этой функции.
Рассмотрим шар (в смысле меры различия  ) радиуса
) радиуса  с центром в
с центром в  :
:
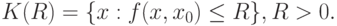
В соответствии с условием теоремы 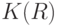 как подпространство топологического пространства
как подпространство топологического пространства  является бикомпактным. Рассмотрим произвольную точку
является бикомпактным. Рассмотрим произвольную точку  из
из  . Справедливо разложение
. Справедливо разложение
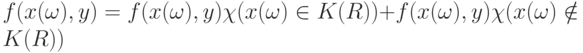
где 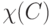 - индикатор множества
- индикатор множества  . Следовательно,
. Следовательно,
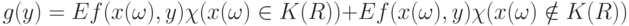 |
( 7) |
Рассмотрим второе слагаемое в (7). В силу (5)
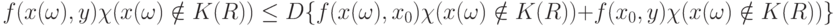 |
( 8) |
Возьмем математическое ожидание от обеих частей (8):
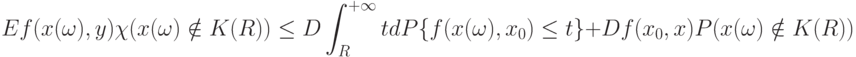 |
( 9) |
В правой части (9) оба слагаемых стремятся к 0 при безграничном возрастании  : первое - в силу того, что
: первое - в силу того, что

второе - в силу того, что распределение случайного элемента 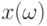 сосредоточено на
сосредоточено на  и
и

Пусть 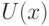 - такая окрестность
- такая окрестность  (т.е. открытое множество, содержащее
(т.е. открытое множество, содержащее  ), для которой
), для которой
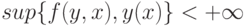
Имеем
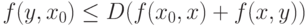 |
( 10) |
В силу (9) и (10) при безграничном возрастании 
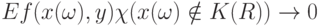 |
( 11) |
равномерно по 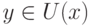 . Пусть
. Пусть 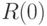 таково, что левая часть (11) меньше
таково, что левая часть (11) меньше  при
при 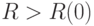 и, кроме того,
и, кроме того,  . Тогда при
. Тогда при 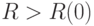
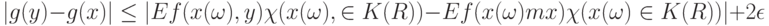 |
( 12) |
Нас интересует поведение выражения в правой части формулы (12) при  . Рассмотрим
. Рассмотрим 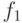 - сужение функции
- сужение функции  на замыкание декартова произведения множеств
на замыкание декартова произведения множеств  , и случайный элемент
, и случайный элемент 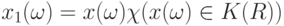 Тогда
Тогда

при 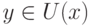 , а непрерывность функции
, а непрерывность функции 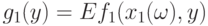 была доказана в теореме 1. Последнее означает, что существует окрестность
была доказана в теореме 1. Последнее означает, что существует окрестность 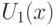 точки
точки  такая, что
такая, что
 |
( 13) |
при 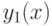 . Из (12) и (13) вытекает, что при
. Из (12) и (13) вытекает, что при 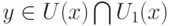
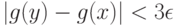
что и доказывает непрерывность функции 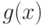 .
.
Докажем существование математического ожидания 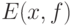 . Пусть
. Пусть 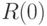 таково, что
таково, что
 |
( 14) |
Пусть  - некоторая константа, значение которой будет выбрано позже. Рассмотрим точку
- некоторая константа, значение которой будет выбрано позже. Рассмотрим точку  из множества
из множества  - дополнения
- дополнения 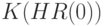 , т.е. из внешности шара радиуса
, т.е. из внешности шара радиуса 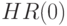 с центром в
с центром в 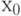 . Пусть
. Пусть 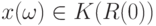 Тогда имеем
Тогда имеем
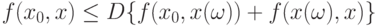
откуда
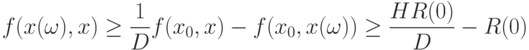 |
( 15) |
Выбирая  достаточно большим, получим с учетом условия (14), что при
достаточно большим, получим с учетом условия (14), что при 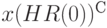 справедливо неравенство
справедливо неравенство
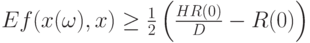 |
( 16) |
Можно выбрать  так, чтобы правая часть (16) превосходила
так, чтобы правая часть (16) превосходила 
Сказанное означает, что 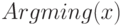 достаточно искать внутри бикомпактного множества
достаточно искать внутри бикомпактного множества 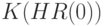 . Из непрерывности функции
. Из непрерывности функции  вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем
вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем  . Существование (непустота) теоретического среднего
. Существование (непустота) теоретического среднего 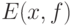 доказана.
доказана.
Докажем существование эмпирического среднего 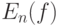 . Есть искушение проводить его дословно так же, как и доказательство существования математического ожидания
. Есть искушение проводить его дословно так же, как и доказательство существования математического ожидания 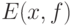 , лишь с заменой 1/2 в формуле (16) на частоту попадания элементов выборки
, лишь с заменой 1/2 в формуле (16) на частоту попадания элементов выборки  в шар
в шар 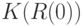 , каковая, очевидно, стремится к вероятности попадания случайного элемента
, каковая, очевидно, стремится к вероятности попадания случайного элемента 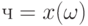 в
в 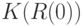 , большей 1/2 в соответствии с (14). Однако это рассуждение показывает лишь, что вероятность непустоты
, большей 1/2 в соответствии с (14). Однако это рассуждение показывает лишь, что вероятность непустоты 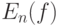 стремится к 1 при безграничном росте объема выборки. Точнее, оно показывает, что
стремится к 1 при безграничном росте объема выборки. Точнее, оно показывает, что
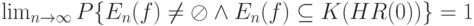
Поэтому пойдем другим путем, не опирающимся к тому же на вероятностную модель выборки. Положим
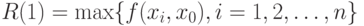 |
( 17) |
Если  входит в дополнение шара
входит в дополнение шара 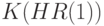 , то аналогично (15) имеем
, то аналогично (15) имеем
 |
( 18) |
При достаточно большом  из (17) и (18) следует, что
из (17) и (18) следует, что
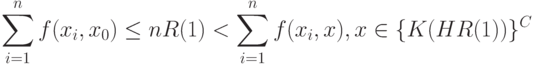
Следовательно,  достаточно искать на
достаточно искать на 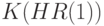 . Заключение теоремы 2 следует из того, что на бикомпактном пространстве
. Заключение теоремы 2 следует из того, что на бикомпактном пространстве 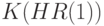 минимизируется непрерывная функция.
минимизируется непрерывная функция.
Теорема 2 полностью доказана.

