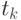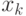| ВКР |
Основы эконометрических методов
Основы линейного регрессионного анализа
Метод наименьших квадратов, рассмотренный в простейшем случае, допускает различные обобщения. Например, метод наименьших квадратов дает алгоритм расчетов, если исходные данные - по-прежнему набор  пар чисел
пар чисел  , где
, где  - независимая переменная (например, время), а
- независимая переменная (например, время), а  - зависимая (например, индекс инфляции), а восстанавливать надо не линейную зависимость, а квадратическую:
- зависимая (например, индекс инфляции), а восстанавливать надо не линейную зависимость, а квадратическую:
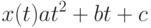
Следует рассмотреть функцию трех переменных

Оценки метода наименьших квадратов - это такие значения параметров  , при которых функция
, при которых функция 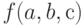 достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции
достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции 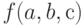 по аргументам
по аргументам 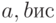 , приравнять их 0, затем из полученных уравнений найти оценки: Имеем:
, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:

Приравнивая частную производную к 0, получаем линейное уравнение относительно трех неизвестных параметров a,b,c:
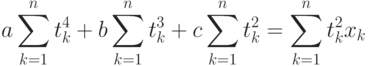
Приравнивая частную производную по параметру  к 0, аналогичным образом получаем уравнение
к 0, аналогичным образом получаем уравнение
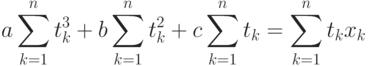
Наконец, приравнивая частную производную по параметру с к 0, получаем уравнение
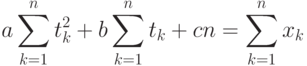
Решая систему трех уравнений с тремя неизвестными, находим оценки метода наименьших квадратов.
Другие задачи, рассмотренные в предыдущем пункте (доверительные границы для параметров и прогностической функции и др.), также могут быть решены. Соответствующие алгоритмы более громоздки. Для их записи полезен аппарат матричной алгебры (см., например, одну из лучших в этой области монографий). Для реальных расчетов используют соответствующие компьютерные программы.
Раздел эконометрики, посвященный восстановлению зависимостей, называется регрессионным анализом. Термин "линейный регрессионный анализ" используют, когда рассматриваемая функция линейно зависит от оцениваемых параметров (от независимых переменных зависимость может быть произвольной). Теория оценивания неизвестных параметров хорошо развита именно в случае линейного регрессионного анализа. Если же линейности нет и нельзя перейти к линейной задаче, то, как правило, хороших свойств от оценок ожидать не приходится.
Продемонстрируем подходы в случае зависимостей различного вида. Если зависимость имеет вид многочлена (полинома)
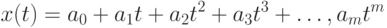
то коэффициенты многочлена могут быть найдены путем минимизации функции
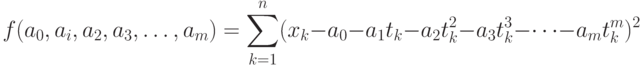
Функция от  не обязательно должна быть многочленом. Можно, например, добавить периодическую составляющую, соответствующую сезонным колебаниям. Хорошо известно, например, что инфляция (рост потребительских цен) имеет четко выраженный годовой цикл - в среднем цены быстрее всего растут зимой, в декабре - январе, а медленнее всего (иногда в среднем даже падают) летом, в июле - августе. Пусть для определенности
не обязательно должна быть многочленом. Можно, например, добавить периодическую составляющую, соответствующую сезонным колебаниям. Хорошо известно, например, что инфляция (рост потребительских цен) имеет четко выраженный годовой цикл - в среднем цены быстрее всего растут зимой, в декабре - январе, а медленнее всего (иногда в среднем даже падают) летом, в июле - августе. Пусть для определенности
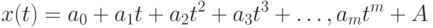
тогда неизвестные параметры могут быть найдены путем минимизации функции
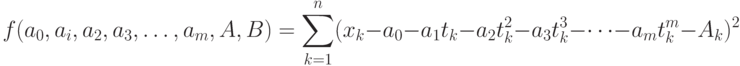
Пусть 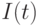 -индекс инфляции в момент
-индекс инфляции в момент  . Принцип стабильности условий приводит к гипотезе о постоянстве темпов роста средних цен, т.е. индекса инфляции. Таким образом, естественная модель для индекса инфляции - это
. Принцип стабильности условий приводит к гипотезе о постоянстве темпов роста средних цен, т.е. индекса инфляции. Таким образом, естественная модель для индекса инфляции - это

Эта модель не является линейной, метод наименьших квадратов непосредственно применять нельзя. Однако если прологарифмировать обе части предыдущего равенства:
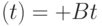
то получим линейную зависимость, рассмотренную выше.
Независимых переменных может быть не одна, а несколько. Пусть, например, по исходным данным 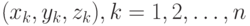 требуется оценить неизвестные параметры a и b в зависимости
требуется оценить неизвестные параметры a и b в зависимости

где  - погрешность. Это можно сделать, минимизировав функцию
- погрешность. Это можно сделать, минимизировав функцию
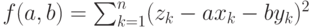
Зависимость от х и у не обязательно должна быть линейной. Предположим, что из каких-то соображений известно, что зависимость должна иметь вид

тогда для оценки пяти параметров необходимо минимизировать функцию
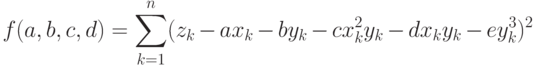
Более подробно рассмотрим пример из микроэкономики. В одной из оптимизационных моделей поведения фирмы используется т.н. производственная функция  , задающая объем выпуска в зависимости от затрат капитала
, задающая объем выпуска в зависимости от затрат капитала  и труда
и труда  . В качестве конкретного вида производственной функции часто используется так называемая функция Кобба-Дугласа
. В качестве конкретного вида производственной функции часто используется так называемая функция Кобба-Дугласа

Однако откуда взять значения параметров  и
и 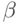 ? Естественно предположить, что они - одни и те же для предприятий отрасли. Поэтому целесообразно собрать информацию
? Естественно предположить, что они - одни и те же для предприятий отрасли. Поэтому целесообразно собрать информацию 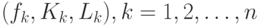 где
где  - объем выпуска на k-ом предприятии,
- объем выпуска на k-ом предприятии, 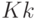 - объем затрат капитала на k-ом предприятии,
- объем затрат капитала на k-ом предприятии, 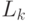 - объем затрат труда на k-ом предприятии (в кратком изложении не пытаемся дать точных определений используемым понятиям из экономики предприятия). По собранной информации естественно попытаться оценить параметры
- объем затрат труда на k-ом предприятии (в кратком изложении не пытаемся дать точных определений используемым понятиям из экономики предприятия). По собранной информации естественно попытаться оценить параметры  и
и 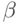 . Но они входят в зависимость нелинейно, поэтому сразу применить метод наименьших квадратов нельзя. Помогает логарифмирование:
. Но они входят в зависимость нелинейно, поэтому сразу применить метод наименьших квадратов нельзя. Помогает логарифмирование:
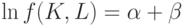
Следовательно, целесообразно сделать замену переменных
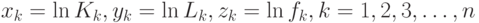
а затем находить оценки параметров  и
и 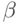 , минимизируя функцию
, минимизируя функцию
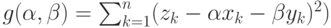
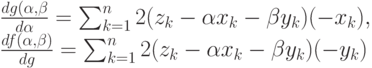
Приравняем частные производные к 0, сократим на 2, раскроем скобки, перенесем свободные члены вправо. Получим систему двух линейных уравнений с двумя неизвестными:

Таким образом, для вычисления оценок метода наименьших квадратов необходимо найти пять сумм
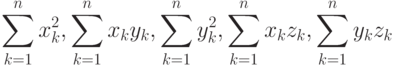
Для упорядочения расчета этих сумм может быть использована таблица типа той, что применялась выше. Отметим, что рассмотренная там постановка переходит в разбираемую сейчас при 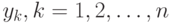
Подходящая замена переменных во многих случаях позволяет перейти к линейной зависимости. Например, если
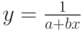
то замена  приводит к линейной зависимости
приводит к линейной зависимости 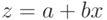 . Если
. Если  , то замена
, то замена 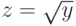 приводит к линейной зависимости
приводит к линейной зависимости 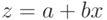 .
.
Регрессионному анализу (т.е методам восстановления зависимостей) посвящена огромная литература. Он хорошо представлен в программных продуктах по анализу данных, особенно та его часть, которая связана с методом наименьших квадратов. Обзор современных эконометрических методов и моделей дан в учебнике.
Контрольные вопросы
- Расскажите об эконометрике в России и за рубежом.
- Что такое "высокие статистические технологии"?
- Почему необходима эконометрическая поддержка принятия решений в менеджменте?
-
Исходные данные - набор
 пар чисел
пар чисел  , где
, где  - независимая переменная (например, время), а
- независимая переменная (например, время), а  - зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостью
- зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостью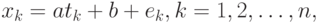
где
 и
и  - параметры, неизвестные статистику и подлежащие оцениванию, а
- параметры, неизвестные статистику и подлежащие оцениванию, а  - погрешности, искажающие зависимость.
- погрешности, искажающие зависимость.Методом наименьших квадратов оцените параметры a и b линейной зависимости. Выпишите восстановленную зависимость.
Вычислите восстановленные значения зависимой переменной, сравните их с исходными значениями (найдите разности) и проверьте условие точности вычислений (при отсутствии ошибок в вычислениях сумма исходных значений должна равняться сумме восстановленных).
Найдите остаточную сумму квадратов и оцените дисперсию погрешностей.
Выпишите точечный прогноз, а также верхнюю и нижнюю доверительные границы для него (для доверительной вероятности 0,95).
Рассчитайте прогнозное значение и доверительные границы для него для момента t = 12.
Как изменятся результаты, если доверительная вероятность будет увеличена? А если она будет уменьшена?
- Как в методе наименьших квадратов используются преобразования переменных?
Темы докладов, рефератов, исследовательских заданий
- Примеры практического использования эконометрических методов.
- Создание и развитие статистики нечисловых данных в России.
- Разработайте алгоритмы расчета доверительных границ и проверки гипотез для непараметрической модели метода наименьших квадратов в случае линейной функции одной переменной.
- Докажите, что сумма исходных значений зависимой переменной должны быть равна сумме восстановленных значений.
- Критерии качества регрессионной модели.
- Использование непараметрических оценок плотности для восстановления зависимости.