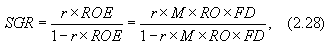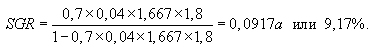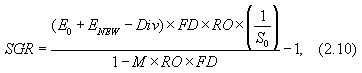| Можно как-то просмотреть результаты тестов после их завершения и завершения всего курса |
Финансовое планирование и прогнозирование
В качестве примера моделирования можно привести имитационную модель прибыли. В укрупненном виде модель представляет собой многомерную таблицу важнейших показателей деятельности объекта в динамике. В подлежащем таблицы находятся взаимоувязанные показатели в номенклатуре статей формы № 2 или более детализированном виде. В сказуемом таблицы находятся результаты прогнозных расчетов по схеме "что будет, если...".
Таким образом, в режиме имитации в модель вводятся прогнозные значения факторов в различных комбинациях, в результате чего рассчитывается ожидаемое значение прибыли.
По результатам имитации может выбираться один или несколько вариантов действий; при этом значения факторов, использованные в процессе моделирования, будут служить прогнозными ориентирами в последующих действиях. Модель реализуется на персональном компьютере в среде табличного процессора в соответствии с намеченным сценарием. Пример имитационной модели прибыли см. в табл. 2.17.
| Показатели | Базовое значение 2004 г. | Расчетное значение | |||
|---|---|---|---|---|---|
| 2005 г. | 2006 г. | ... | 2009 г. | ||
|
|||||
Другим примером метода моделирования служат модели факторных связей по схеме фирмы Du Pont - базовая (2.6) и модифицированная (2.7):
ROA = M x RO = (NP/S) x (S/A) (2.6)
ROE = ROA x FD = M x RO x FD = (NP/S) x (S/A) x (A/E), (2.7)
| где | ROA | - | рентабельность активов, ROA = NP/А; |
| RO | - | коэффициент оборачиваемости активов, ресурсоотдача; | |
| NP | - | чистая прибыль; | |
| А | - | активы; | |
| ROE | - | рентабельность акционерного (собственного) капитала, ROE = NP/E; | |
| FD | - | финансовый рычаг, мультипликатор собственного капитала; | |
| E | - | акционерный Подставляя в модель прогнозные значения таких факторов, как объем продаж, себестоимость, основные и оборотные средства, величину заемного капитала и др., можно представить прогноз двух важнейших показателей эффективности - рентабельности авансированного и собственного капитала. |
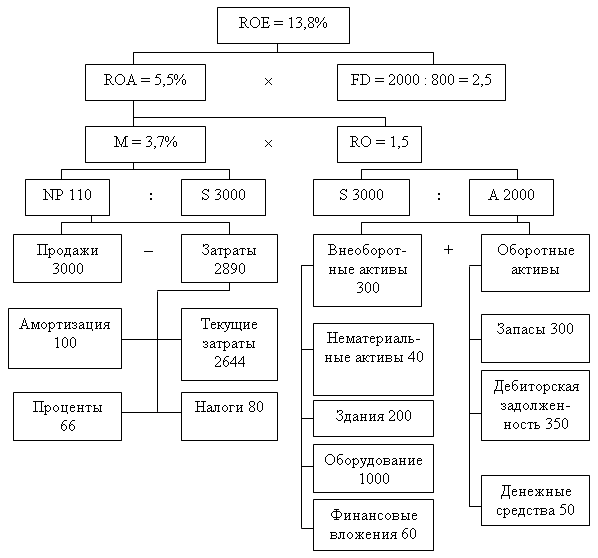
Рисунок 2.2 иллюстрирует взаимосвязь важнейших компонент модифицированной формулы "Du Pont" и возможность моделирования требуемой величины рентабельности акционерного капитала (активы, продажи, затраты - в млн д. е.).
Руководство может воспользоваться схемой фирмы "Du Pont" для анализа путей повышения степени эффективности функционирования предприятия. С помощью показателей левой части схемы специалисты по сбыту могут изучать, какое влияние на рентабельность оказывает увеличение цен реализации (или снижение их для стимулирования спроса на продукцию), изменение ассортимента продукции, выход на новые рынки сбыта и т. д. Для бухгалтеров больший интерес представляет анализ расходных статей и поиск путей снижения себестоимости продукции. Правая часть схемы представляет интерес для финансовых аналитиков, менеджеров по производству и маркетингу, которые должны изыскивать пути оптимизации уровня тех или иных видов активов. Что касается финансового менеджера, то он может провести сравнительный анализ использования различных стратегий финансирования, попытаться найти возможности снижения расходов по обязательным процентным платежам, оценить степень риска в случае привлечения дополнительных внешних источников финансирования, необходимых для повышения рентабельности собственного капитала.
Модифицированная формула Du Pont лежит в основе моделирования достижимого роста предприятия (SGR), который зависит от рентабельности собственного капитала (ROE) и коэффициента реинвестирования прибыли (r):
| где | SGR (sustainable growth rаte) | - | максимально достижимый годовой прирост объема продаж; |
| r | - | целевое значение коэффициента реинвестирования прибыли; | |
| r | = | 1 - d (d - целевое значение нормы выплаты дивидендов). |
Это модель устойчивого состояния, в которой будущее совершенно аналогично прошлому в отношении баланса и показателей эффективности работы предприятия. При составлении этой модели также изначально предполагается, что предприятие не привлекает средства извне, выпуская новые акции; собственный капитал увеличивается только путем накопления прибыли.
Модель является жестко детерминированной факторной моделью, устанавливающей зависимость между темпом прироста экономического потенциала предприятия, выражающегося в наращивании объемов производства, и основными факторами, его определяющими. Эти факторы дают обобщенную и комплексную характеристику различных сторон финансово-хозяйственной деятельности предприятия: производственной (ресурсоотдача), финансовой (структура источников средств), взаимоотношений владельцев и управленческого персонала (дивидендная политика), положения предприятия на товарном рынке (рентабельность продукции).
Например, деятельность предприятия характеризуется следующими плановыми данными: рентабельность продаж М = 0,04; коэффициент реинвестирования прибыли r = 0,7; оборачиваемость активов RO = 1,667; соотношение величины заемных (D) и собственных (Е) средств  , отсюда:
, отсюда:
В этом случае достижимый уровень роста:
Таким образом, 9,17% - это достижимый прирост объема продаж, если предприятие не меняет сложившуюся структуру активов, источников средств, использования прибыли.
Если же владельцы и руководство предприятия намерены наращивать потенциал более высокими темпами, они могут сделать это за счет одного или нескольких факторов:
- изменения дивидендной политики (уменьшения доли чистой прибыли, выплачиваемой в виде дивидендов);
- изменения финансовой политики (повышения доли привлеченных средств в общей сумме капитала);
- повышения оборачиваемости активов (рост ресурсоотдачи за счет интенсификации производственной деятельности);
- увеличения рентабельности продукции за счет относительного сокращения издержек производства и реализации.
Моделирование уровня достижимого роста при изменяющихся переменных осуществляется по-другому:
| где | E0 | - | акционерный (собственный) капитал в отчетном году, млн д. е.; |
| ENEW | - | поступления от продажи акций в планируемом году, млн д. е.; | |
| S0 | - | объем продаж в отчетном году, млн д. е.; | |
| Div | - | плановая сумма годовых дивидендов, млн д. е. |
Например, Е0 = 100 млн д. е., ENEW = 10 млн д. е., Div = 3,93 млн д. е., S0 = 300 млн д. е., М = 0,04, RO = 1, 6667, FD = 1,8. Тогда:
Этот показатель SGR выше прежнего из-за новых вливаний собственного капитала.
Предположим теперь, что ENEW = 0, Div = 4 млн д. е. и запланированы повышенными все коэффициенты: М = 0,05, FD = 2,0, RO = 1,8182. Тогда:
Такой существенный рост возможен благодаря повышению эффективности деятельности, что дает больше нераспределенной прибыли, и более высокому коэффициенту привлечения заемного капитала.
Имея любые пять из шести переменных, данные о начальном собственном капитале и начальном объеме продаж, можно найти шестую переменную. В табл. 2.18 представлен конкретный пример моделирования. Недостающие переменные, которые следует найти, выделены:
| Переменные | A/S (1/RO) | NP/S | D/E | Div | ENEW | SGR |
| 1 | 0,60 | 0,04 | 0,80 | 4,00 | 0,00 | 0,0909 |
| 2 | 0,60 | 0,04 | 0,80 | 4,00 | 10,00 | 0,2046 |
| 3 | 0,55 | 0,05 | 1,00 | 4,00 | 0,00 | 0,4222 |
| 4 | 0,50 | 0,05 | 0,50 | 4,00 | 0,00 | 0,1294 |
| 5 | 0,65 | 0,035 | 0,80 | 4,00 | 5,00 | 0,0325 |
| 6 | 0,70 | 0,03 | 0,80 | 4,00 | 0,00 | -0,1083 |
| 7 | 0,50 | 0,05 | 0,50 | 4,00 | 10,00 | 0,25 |
| 8 | 0,4292 | 0,04 | 0,50 | 4,00 | 10,00 | 0,3 |
| 9 | 0,5263 | 0,0623 | 0,60 | 4,00 | 0,00 | 0,2 |
| 10 | 0,60 | 0,0538 | 1,00 | 4,00 | 0,00 | 0,3 |
| 11 | 0,5882 | 0,05 | 0,7682 | 4,00 | 10,00 | 0,25 |
| 12 | 0,60 | 0,04 | 1,0272 | 4,00 | 0,00 | 0,25 |
| 13 | 0,60 | 0,04 | 1,1659 | 4,00 | 0,00 | 0,35 |