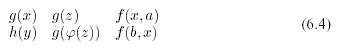Сентенциальное программирование: PROLOG

Управление исполнением программы

Джулией Робинсон доказано (см., напр. [ 30 ] ), что для выражений первого порядка имеется эффективный алгоритм унификации, находящий для двух выражений унифицирующую подстановку либо обосновывающий, что такой подстановки нет.

Пример 6.3.1. Две последовательности выражений

где a, b — константы, а латинские буквы из конца алфавита — переменные, унифицируются в

подстановкой

А в двух последовательностях

никакие два соответственных выражения унифицированы быть не могут.

Уже в приведенном примере видно, что унификация — глобальная операция.

Заметим, что логический алгоритм унификации обладает свойством частичного исполнения: если унифицировать две подструктуры, то после исполнения унифицирующей подстановки можно продолжить унификацию остальных подструктур, и результат унификации не изменится. Так что выражения могут унифицироваться одно за другим

Более того, можно было бы унифицировать любые соответственные друг другу внутренние подвыражения в произвольном порядке, лишь бы объемлющие унифицировались после подчиненных. Автору неизвестно ни одно использование этого естественного и многообещающего обобщения алгоритма унификации.

В первой реализации языка PROLOG, основные особенности которой стали в дальнейшем фактическим стандартом, создатели допустили ошибку в понимании и, соответственно, в реализации алгоритма унификации, которая, к примеру, разрушает свойство частичного исполнения и может привести к излишней конкретизации, в то время как можно было бы найти более общую конкретизирующую подстановку. Эта ошибка несущественна, она не влияет на подавляющее большинство программ, но иногда она приводит к появлению бесконечных термов, и некоторые реализаторы языка PROLOG с гордостью пишут, что они умеют печатать и показывать на экране даже такие термы.

Желающие в качестве упражнения выловить ошибку самостоятельно, сравните алгоритмы унификации, описанные в книге [ 30 ] и [ 12 ] .

Рассмотрим, как исполняется программа на языке PROLOG. В программе может быть одно целевое предложение, не имеющее головной части. Оно начинается с функтора :- или ?-. В программе, транслируемой и исполняемой в пакетном режиме, обычно используется первый функтор, а при задании цели с терминала в режиме диалога—второй. Разница между ними проявляется лишь в режиме диалога. Второй вариант цели позволяет пользователю после нахождения одного из решений продолжить выполнение программы для поиска следующего решения. Первый такой возможности ему не представляет, программа находит какое-нибудь решение и останавливается.

Исходная цель называется запросом. Переменные, входящие в запрос, носят особый статус. Их значения в ходе последовательных унификаций накапливаются в скрытой части поля памяти программы и при успешном исполнении выдаются в качестве ответа на запрос.

В каждый момент рассматривается первый из термов цели. Если его детерминатив не является встроенной функцией или встроенным оператором с особым определением, то ищется предложение, голова которого унифицируется с этим термом. При этом прежде всего проверяется наличие предложений, детерминатив которых совпадает с детерминативом первого терма. Если таких предложений несколько, то создается точка возврата, в которой запоминается состояние программы для отработки возможных неудач.

Предложения испытываются, начиная с первого. Полученная унифицирующая подстановка применяется ко всем термам в поле зрения и к хвосту успешно унифицированного предложения. После этого хвост заменяет унифицированную голову, и выполнение возобновляется. Исполнение считается успешным, если на некотором шаге цель исчезает. Исполнение считается неудачным, если в некоторый момент для первого из термов не найдется унифицируемого с ним предложения.

Заметим, что переменные предыдущих унификаций отождествляются с переменными следующих унификаций лишь в том случае, если эти переменные дожили в поле зрения до соответствующей унификации. Если переменная уже получила постоянное значение либо значение, в котором она не встречается, то в последующем переменные с тем же именем трактуются как новые. Таким образом, конкретные имена переменных имеют значение лишь внутри одного предложения.

Если исполнение оказалось неудачным, то программа возвращается к последней из точек возврата (происходит откат ) и испытывается следующее по порядку предложение с тем же детерминативом. Если таких предложений больше не осталось, то происходит откат к следующей точке возврата, и так далее. Если исполнение откатилось до запроса и больше кандидатов на унификацию не осталось, программа заканчивается общей неудачей.

Стандартным ответом программы на запрос служит Yes, если программа закончилась удачно, и No, если она закончилась неудачно. При удаче выводятся значения всех переменных исходного запроса.

Так, например, если программа и ее база данных имеют вид

greater(X,Y):-greater1(X,Y).
greater(X,Y):-greater1(Z,Y),greater(X,Z).
greater1(X,f(X)).
estimation(X,Y):-greater(X,Y),known(Y).
known(f(f(f(f(a))))).
unknown(a).
unknown(b).

то ответом на запрос

?-unknown(Y),estimation(Y,X).

будет

Y=a
X=(f(f(f(f(a))))
Yes

а при попытке ответа на запрос

?-estimation(b,X).

программа зациклится.

Насколько каверзны вроде бы невинные предположения (например, условие, что подцели достигаются строго одна за другой и варианты перебираются в том же порядке), сделанные в языке PROLOG, видно из того, что при логически эквивалентной переформулировке одного из предложений программы

estimation(X,Y):-known(Y),greater(X,Y).

программа успешно ответит на второй запрос

No

Еще более впечатляющий пример рассмотрен в упражнении 5.

Есть еще одна особенность языка PROLOG, которая кажется явным ляпсусом, но на самом деле является отражением результата Косовского и др. (неизвестного реализаторам и пользователям языка PROLOG, но лучшими из них ощущаемого интуитивно) о несовместимости моделей отождествления PROLOG и Рефала. Вся работа системы PROLOG основана на предположении, что значения унифицируемых переменных набираются однозначно, и следующий вариант может получиться лишь в результате унификации с другим фактом либо предложением. Поэтому когда (как в случае со списками или строками) PROLOG встречается с неоднозначным отождествлением, он никогда не будет перебирать разные его варианты. Он либо выберет первый из них (например, при унификации неизвестных [X|Y] с уже известным списком Z X будет пустым списком), либо зациклится на бесконечном повторении одного и того же варианта (смотри предыдущую скобку, которая иллюстрирует сразу две неприятности: если к такой унификации вернутся, будет выбран 'новый' пустой список в качестве X ).

Для того, чтобы вычислить выражение, имеется предопределенная бинарная операция is. Она должна иметь вторым аргументом выражение, составленное из атомов при помощи функций. После применения X is 1+2 вместо X подставится 3. Даже выражение 1+2 остается в таком же виде, пока оно не попадет во второй аргумент is.

Внимание!

То, что некоторый функтор определен как операция, не значит, что он вычисляется. Это просто изменение конкретно-синтаксического представления. Для того чтобы иметь возможность вычислить выражение, нужно определить функтор как внутреннюю или внешнюю функцию. При этом необязательно делать его операцией.