Протоколирование и аудит, шифрование, контроль целостности
Контроль целостности
Криптографические методы позволяют надежно контролировать целостность как отдельных порций данных, так и их наборов (таких как поток сообщений); определять подлинность источника данных; гарантировать невозможность отказаться от совершенных действий ("неотказуемость").
В основе криптографического контроля целостности лежат два понятия:
- хэш-функция;
- электронная цифровая подпись (ЭЦП).
Хэш-функция – это труднообратимое преобразование данных ( односторонняя функция ), реализуемое, как правило, средствами симметричного шифрования со связыванием блоков. Результат шифрования последнего блока (зависящий от всех предыдущих) и служит результатом хэш-функции.
Пусть имеются данные, целостность которых нужно проверить, хэш-функция и ранее вычисленный результат ее применения к исходным данным (так называемый дайджест ). Обозначим хэш-функцию через h, исходные данные – через T, проверяемые данные – через T'. Контроль целостности данных сводится к проверке равенства h(T') = h(T). Если оно выполнено, считается, что T' = T. Совпадение дайджестов для различных данных называется коллизией. В принципе, коллизии, конечно, возможны, поскольку мощность множества дайджестов меньше, чем мощность множества хэшируемых данных, однако то, что h есть функция односторонняя, означает, что за приемлемое время специально организовать коллизию невозможно.
Рассмотрим теперь применение асимметричного шифрования для выработки и проверки электронной цифровой подписи. Пусть E(T) обозначает результат зашифрования текста T с помощью открытого ключа, а D(T) – результат расшифрования текста Т (как правило, шифрованного) с помощью секретного ключа. Чтобы асимметричный метод мог применяться для реализации ЭЦП, необходимо выполнение тождества
E(D(T)) = D(E(T)) = T
На рис. 11.5 показана процедура выработки электронной цифровой подписи, состоящая в шифровании преобразованием D дайджеста h(T).
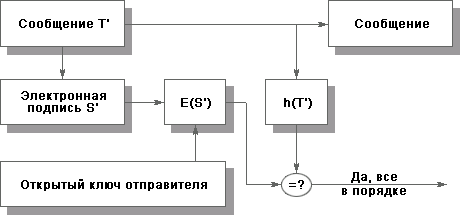
Проверка ЭЦП может быть реализована так, как показано на рис. 11.6.
Из равенства
E(S') = h(T')
следует, что S' = D(h(T')) (для доказательства достаточно применить к обеим частям преобразование D и вычеркнуть в левой части тождественное преобразование D(E())). Таким образом, электронная цифровая подпись защищает целостность сообщения и удостоверяет личность отправителя, то есть защищает целостность источника данных и служит основой неотказуемости.
Стандарт ГОСТ Р 34.11-2012 "Информационная технология (ИТ). Криптографическая защита информации. Функция хэширования" определяет алгоритм и процедуру вычисления хэш-функции для любой последовательности двоичных символов, которые применяются в криптографических методах обработки и защиты информации, в том числе для реализации процедур обеспечения целостности, аутентичности, электронной цифровой подписи (ЭЦП) при передаче, обработке и хранении информации в автоматизированных системах. Межгосудартвенный ГОСТ Р 34.10-2018 "Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи" описывает алгоритмы формирования и проверки электронной цифровой подписи, реализуемой с использованием операций в группе точек эллиптической кривой, определенной над конечным простым полем.
Для контроля целостности последовательности сообщений (то есть для защиты от кражи, дублирования и переупорядочения сообщений) применяют временные штампы и нумерацию элементов последовательности, при этом штампы и номера включают в подписываемый текст.
Цифровые сертификаты
При использовании асимметричных методов шифрования (и, в частности, электронной цифровой подписи) необходимо иметь гарантию подлинности пары (имя пользователя, открытый ключ пользователя). Для решения этой задачи в спецификациях X.509 вводятся понятия цифрового сертификата и удостоверяющего центра.
Удостоверяющий центр – это компонент глобальной службы каталогов, отвечающий за управление криптографическими ключами пользователей.Открытые ключи и другая информация о пользователях хранится удостоверяющими центрами в виде цифровых сертификатов, имеющих следующую структуру:
- порядковый номер сертификата;
- идентификатор алгоритма электронной подписи;
- имя удостоверяющего центра;
- срок годности;
- имя владельца сертификата (имя пользователя, которому принадлежит сертификат);
- открытые ключи владельца сертификата (ключей может быть несколько);
- идентификаторы алгоритмов, ассоциированных с открытыми ключами владельца сертификата;
- электронная подпись, сгенерированная с использованием секретного ключа удостоверяющего центра (подписывается результат хэширования всей информации, хранящейся в сертификате).
Цифровые сертификаты обладают следующими свойствами:
- любой пользователь, знающий открытый ключ удостоверяющего центра, может узнать открытые ключи других клиентов центра и проверить целостность сертификата;
- никто не может модифицировать информацию о пользователе без нарушения целостности сертификата.
В спецификациях X.509 не описывается конкретная процедура генерации криптографических ключей и управления ими, однако даются некоторые общие рекомендации. В частности, оговаривается, что пары ключей могут порождаться любым из следующих способов:
- ключи может генерировать сам пользователь. В таком случае секретный ключ не попадает в руки третьих лиц, однако нужно решать задачу безопасной связи с удостоверяющим центром;
- ключи генерирует доверенное лицо. В таком случае приходится решать задачи безопасной доставки секретного ключа владельцу и предоставления доверенных данных для создания сертификата;
- ключи генерируются удостоверяющим центром. В таком случае остается только задача безопасной передачи ключей владельцу.
Цифровые сертификаты в формате X.509 версии 3 стали не только формальным, но и фактическим стандартом, поддерживаемым многочисленными удостоверяющими центрами.