Регулярные языки и конечные автоматы
Задачи
Задача 5.1. Определите конкатенацию для следующих пар языков L1 и L2:
-
L1= {a, ab, abb} и
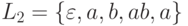 ;
; -
 и L2= { a, b, abb, a} ;
и L2= { a, b, abb, a} ; -
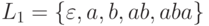 и
и 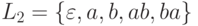 ;
;
Задача 5.2. Пусть L={baa, bab, bba, bbb}. Какой из следующих языков является итерацией L* этого языка?
-
 ;
; -
 ;
; -
 ;
; - { w | w=bw' и | w| >= 12 }.
Задача 5.3. Докажите правильность регулярного выражения в примере 5.4.
Задача 5.4. Докажите следующие эквивалентности для регулярных выражений.
- p*(p+q)* = (p + qp*)* = (p+q)* ;
- p(qp)* = (pq)*p ;
- (p*q*)* =(q*p*)* ;
- (pq)+(q*p* + q*) = (pq)*p q+p*.
Задача 5.5. Постройте регулярное выражение, задающее язык
язык L в алфавите 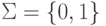 .
.
- L= {w | w содержит нечетное число букв 0 и четное число букв 1}} ;
- L= {w | w содержит подслово 001 или подслово 110 } ;
- L= {w | w содержит по крайней мере мере два подряд идущих 0 } ;
- L= {w | w не содержит подслов 011 и 010}.
Задача 5.6. Определите, какой язык представляется следующими регулярными выражениями.
- (0*1*)0 ;
- (01*)0 ;
- (00 +11 +(01 + 10)(00 +11)+(01+10))*.
Задача 5.7. Упростить следующие регулярные выражения.
- (00*)0 + (00)* ;
-
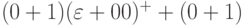 ;
; -
 .
.
Задача 5.8. Выше в задаче 14.5 предлагалось построить автомат-распознаватель, который проверяет правильность сложения. Постройте регулярное выражение, задающее распознаваемый этим автоматом язык S, т.е. следующее множество слов в алфавите {0, 1}3
S= {(x1(1),x2(1),y(1)) (x1(2),x2(2),y(2)) ... (x1(n),x2(n),y(n)) | y = y(n) ... y(2)y(1) - это первые n битов суммы двоичных чисел x1= x1(n)... x1(2)x1(1) и x2 = x2(n)... x2(2)x2(1)}.
Задача 5.9. Пусть Mr - это автомат, который строится в доказательстве теоремы 5.1 по регулярному выражению r. Докажите, что
- у Mr нет переходов из единственного заключительного состояния qf ;
- в диаграмме Mr из каждой вершины выходит не более двух ребер;
- число состояний Mr не более чем вдвое превосходит длину выражения r, т.е. |Q| <= 2 |r|.
Задача 5.10. Примените процедуру детерминизации из теоремы 4.2 и постройте ДКА, эквивалентный НКА  из примера 5.7.
из примера 5.7.
