Центральная предельная теорема
Свойство 27.
- Если
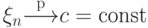 и
и 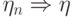 , то
, то 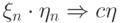 .
. - Если
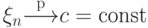 и
и 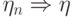 , то
, то 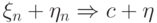 .
.
Доказательство. Нелюбознательный читатель может пропустить это доказательство, вернувшись к нему при втором прочтении.
Заметим вначале, что
если 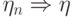 , то
, то  и
и 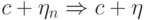 (доказать).
Поэтому
достаточно доказать первое утверждение свойства 27 при
(доказать).
Поэтому
достаточно доказать первое утверждение свойства 27 при 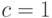 ,
а второе утверждение - при
,
а второе утверждение - при 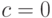 .
.
Рассмотрим второе утверждение, оставив первое любознательному читателю.
Пусть 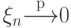 и
и 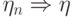 .
Докажем, что тогда
.
Докажем, что тогда 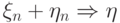 .
.
Пусть  - точка непрерывности функции распределения
- точка непрерывности функции распределения 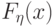 . Требуется доказать, что имеет место
сходимость
. Требуется доказать, что имеет место
сходимость  к
к 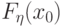 .
Зафиксируем
.
Зафиксируем 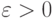 такое,
что
такое,
что 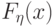 непрерывна в точках
непрерывна в точках 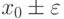 .
.
Cобытия  и
и  образуют полную группу, поэтому
образуют полную группу, поэтому
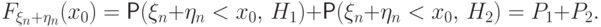
 сверху и снизу. Для
сверху и снизу. Для  имеем
имеем
 сделана сколь угодно
малой. Для
сделана сколь угодно
малой. Для  , с одной стороны,
, с одной стороны,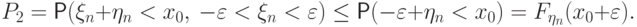
 и
и 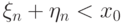 , то
тем более
, то
тем более 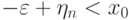 .
С другой стороны,
.
С другой стороны,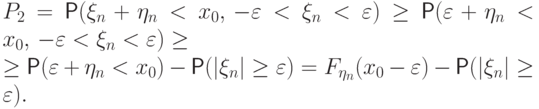
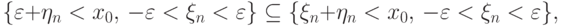
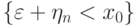 числа
числа 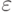 на меньшую величину
на меньшую величину 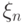 ,
, 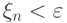 .
Второе неравенство следует из свойств:
.
Второе неравенство следует из свойств:
Мы получили оценки снизу и сверху для  , т.е.
для
, т.е.
для  :
:
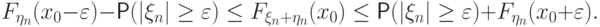
 к бесконечности и вспоминая, что
к бесконечности и вспоминая, что  -
точки непрерывности функции распределения
-
точки непрерывности функции распределения 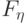 , получаем
, получаем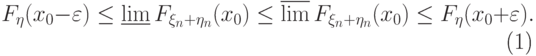 |
( 24) |
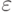 , что в точках
, что в точках  функция
распределения
функция
распределения 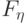 будет непрерывной и, следовательно, останутся верны неравенства
(24). Переходя к пределу по такой
последовательности
будет непрерывной и, следовательно, останутся верны неравенства
(24). Переходя к пределу по такой
последовательности 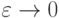 и помня, что
и помня, что  - точка непрерывности функции
- точка непрерывности функции 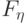 ,
получаем, что нижний и верхний пределы
,
получаем, что нижний и верхний пределы  при
при 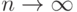 совпадают и равны
совпадают и равны 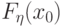 .
.В качестве простого следствия из только что доказанного второго утверждения
свойства 27 покажем, что
сходимость 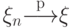 по
вероятности влечет слабую сходимость
по
вероятности влечет слабую сходимость  .
.
Представим 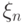 в виде суммы
в виде суммы 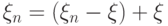 . Здесь
последовательность
. Здесь
последовательность 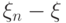 по вероятности стремится к нулю, а
"последовательность"
по вероятности стремится к нулю, а
"последовательность"  слабо сходится к
слабо сходится к  . Поэтому их сумма слабо
сходится к
. Поэтому их сумма слабо
сходится к  ,
что и требовалось доказать.
,
что и требовалось доказать.
Основной источник слабо сходящихся последовательностей и необычайно мощное и универсальное средство для асимптотического анализа распределений сумм независимых и одинаково распределенных случайных величин предоставляет нам центральная предельная теорема.
