Теория трансверсалей
Доказательство. Очевидно, что словарный ранг не может превосходить
числа  .
Чтобы доказать равенство, можно без потери общности предположить, что все
единицы из
.
Чтобы доказать равенство, можно без потери общности предположить, что все
единицы из  содержатся в
содержатся в  строках
и
строках
и  столбцах (где
столбцах (где 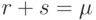 ) и
что строки и столбцы расположены в таком порядке, что в нижнем левом углу
матрицы А находится
) и
что строки и столбцы расположены в таком порядке, что в нижнем левом углу
матрицы А находится 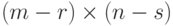 -подматрица, полностью
состоящая из нулей.
-подматрица, полностью
состоящая из нулей.
Если  , то определим
, то определим  как множество целых
чисел
как множество целых
чисел 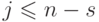 , таких, что
, таких, что 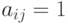 . Нетрудно проверить, что
объединение любых
. Нетрудно проверить, что
объединение любых  множеств
множеств  содержит по меньшей
мере
содержит по меньшей
мере  целых чисел;
поэтому семейство
целых чисел;
поэтому семейство 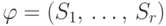 имеет трансверсаль.
Отсюда следует, что подматрица
имеет трансверсаль.
Отсюда следует, что подматрица  из
из  содержит
множество из
содержит
множество из  единиц, никакие две из которых не принадлежат одной
и той же строке или
одному и тому же столбцу. Аналогично, матрица
единиц, никакие две из которых не принадлежат одной
и той же строке или
одному и тому же столбцу. Аналогично, матрица  содержит множество
из
содержит множество
из  единиц, обладающих тем же свойством. Таким образом,
матрица
единиц, обладающих тем же свойством. Таким образом,
матрица  содержит множество из
содержит множество из  единиц, никакие
две из которых не принадлежат одной и той же строке или одному и тому же столбцу. Тем самым
показано, что
единиц, никакие
две из которых не принадлежат одной и той же строке или одному и тому же столбцу. Тем самым
показано, что  не превосходит словарного ранга.
не превосходит словарного ранга.
Мы только что доказали теорему Кенига-Эгервари с помощью теоремы Холла, а доказательство теоремы Холла с помощью теоремы Кенига-Эгервари и того проще. Следовательно, эти две теоремы в некотором смысле эквивалентны. В лекции 17 мы докажем теорему о максимальном потоке и минимальном разрезе, которая тоже эквивалентна теореме Холла.
Общие
трансверсали. Если  — непустое
конечное множество, а
— непустое
конечное множество, а  и
и 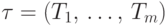 — два семейства его непустых подмножеств, то интересно знать,
когда существует общая трансверсаль для
— два семейства его непустых подмножеств, то интересно знать,
когда существует общая трансверсаль для  и
и  , то есть
множество, состоящее из
, то есть
множество, состоящее из  различных элементов
множества
различных элементов
множества  и являющееся трансверсалью и для
и являющееся трансверсалью и для  , и
для
, и
для 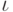 .
.
Сформулируем необходимое и достаточное условие для того, чтобы два
семейства  и
и  имели общую трансверсаль;
заметим, что эта теорема сводится к теореме Холла, если
положить
имели общую трансверсаль;
заметим, что эта теорема сводится к теореме Холла, если
положить  для
для 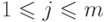 .
.
Теорема
Пусть  — непустое конечное множество, а
— непустое конечное множество, а 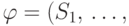
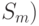 и
и 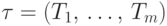 — два семейства его непустых
подмножеств. Тогда
— два семейства его непустых
подмножеств. Тогда  и
и  имеют общую
трансверсаль в том и только в том случае, если для всех
подмножеств
имеют общую
трансверсаль в том и только в том случае, если для всех
подмножеств  и
и  множества
множества 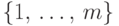
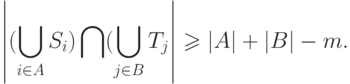
Набросок доказательства. Рассмотрим семейство 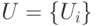 подмножеств множества
подмножеств множества 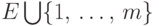 (считаем,
что
(считаем,
что  и
и  не пересекаются), где множеством
индексов также является
не пересекаются), где множеством
индексов также является 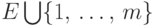 и где
и где 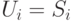 , если
, если 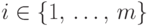 ,
и
,
и 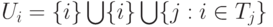 ,
если
,
если 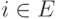 .Нетрудно проверить, что
.Нетрудно проверить, что 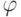 и
и 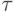 имеют
общую трансверсаль тогда и только тогда, если семейство
имеют
общую трансверсаль тогда и только тогда, если семейство  имеет трансверсаль.
Применяя затем теорему Холла к семейству
имеет трансверсаль.
Применяя затем теорему Холла к семейству  , получим нужный результат.
, получим нужный результат.
Условия, при которых существует общая трансверсаль для трех семейств непустых подмножеств некоторого множества, пока что не известны, и задача нахождения таких условий кажется очень трудной. Многие попытки решения этой задачи используют теорию матроидов; и действительно, некоторые задачи теории трансверсалей становятся почти тривиальными, если рассматривать их с точки зрения теории матроидов.
