Гамильтоновы графы
Пример.
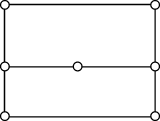
Такие графы называют "тэта графами", поскольку они
похожи на греческую букву  ("тета"). По рисунку видно,
что в таком графе не удается выделить простой цикл, содержащий все вершины.
("тета"). По рисунку видно,
что в таком графе не удается выделить простой цикл, содержащий все вершины.
Выведем еще два достаточных признака гамильтоновых графов.
Рассмотрим граф  с
с 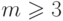 вершинами.
Пронумеруем их произвольным
образом и выпишем их последовательность:
вершинами.
Пронумеруем их произвольным
образом и выпишем их последовательность:
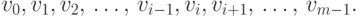 |
( 5.1) |
При этом может случиться, что некоторые две соседние вершины,
например,  и
и 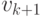 , не связаны ребром. Будем
говорить, что в данной последовательности имеется "разрыв" между
вершинами
, не связаны ребром. Будем
говорить, что в данной последовательности имеется "разрыв" между
вершинами  и
и 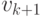 .
.
Очевидно, в последовательности 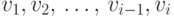 не возникнут другие разрывы, если ее записать в обратном порядке, а
именно:
не возникнут другие разрывы, если ее записать в обратном порядке, а
именно:  ,
, 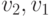 .
.
Пусть для определенности разрыв в последовательности (5.1) имеет место
между вершинами 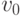 и
и 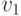 . Положим теперь,
что
. Положим теперь,
что 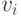 —
вершина графа
—
вершина графа  , связанная ребром с
, связанная ребром с 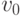 . Число
таких вершин
. Число
таких вершин 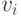 равно
равно 
Пытаясь ликвидировать разрыв в последовательности (5.1) между 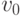 и
и 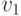 , запишем ее в измененном порядке:
, запишем ее в измененном порядке:
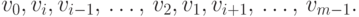 |
( 5.2) |
При этом число разрывов уменьшится на единицу в том случае, если между
вершинами 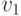 и
и 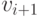 не возникнет новый
разрыв.
не возникнет новый
разрыв.
Вершину 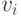 среди
среди 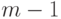 вершин, не совпадающих
с
вершин, не совпадающих
с 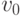 , можно
всегда найти, так, чтобы между
, можно
всегда найти, так, чтобы между 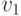 и
и 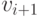 не
возник новый разрыв, если справедливо неравенство
не
возник новый разрыв, если справедливо неравенство
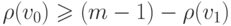
(справа в этом неравенстве читаем число разрывов, которые могут произойти при всевозможных перестановках последовательности (5.1)).
Но вершины 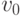 и
и 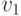 были выбраны
произвольно; можно было
рассмотреть разрыв между другими соседними вершинами
были выбраны
произвольно; можно было
рассмотреть разрыв между другими соседними вершинами  и
и 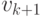 в последовательности (5.1), можно было даже выбрать вершины
в последовательности (5.1), можно было даже выбрать вершины 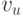 и
и 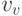 графа
графа  , не стоящие рядом в
последовательности (5.1). Лишь бы
соблюдалось неравенство
, не стоящие рядом в
последовательности (5.1). Лишь бы
соблюдалось неравенство
 |
( 5.3) |
Заметим, что неравенство (5.3) симметрично относительно 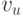 и
и 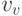 .
Его можно записать в виде
.
Его можно записать в виде
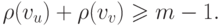 |
( 5.4) |
И тогда
в последовательности (5.1) удастся ликвидировать все разрывы. А это
означает, что в графе  найдется гамильтонов путь.
найдется гамильтонов путь.
Покажем, что если для любой пары вершин 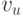 и
и 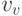 графа
графа  с
с  вершинами справедливо неравенство
вершинами справедливо неравенство
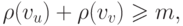 |
( 5.5) |
то граф  обладает гамильтоновым циклом. Это один из
достаточных признаков того, что данный граф является гамильтоновым.
обладает гамильтоновым циклом. Это один из
достаточных признаков того, что данный граф является гамильтоновым.
Рассмотрим гамильтонов путь, связывающий вершины 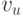 и
и 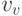 графа
графа  .
.
Пример.
Пусть  — одна из вершин графа
— одна из вершин графа  , связанная
ребром с вершиной
, связанная
ребром с вершиной 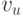 . Тогда в силу неравенства (5.5), хотя бы для одной
из таких вершин
. Тогда в силу неравенства (5.5), хотя бы для одной
из таких вершин  найдется в гамильтоновом пути смежная с ней
вершина
найдется в гамильтоновом пути смежная с ней
вершина 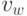 , такая, которая связана ребром
с
, такая, которая связана ребром
с 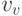 .
.
Добавляя к гамильтонову пути ребра 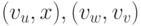 и выбрасывая из него ребро
и выбрасывая из него ребро  , получаем гамильтонов цикл, что
и требовалось.
, получаем гамильтонов цикл, что
и требовалось.
Теперь, как следствие, получаем еще один достаточный признак того, что данный граф является гамильтоновым.
Формулируется этот признак так:
Граф  с
с  вершинами имеет гамильтонов цикл,
если для произвольной
его вершины
вершинами имеет гамильтонов цикл,
если для произвольной
его вершины
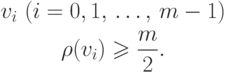 |
( 5.6) |
Хотя этот признак проще, чем предыдущий (при его использовании приходится меньше считать), он позволяет распознать более узкий класс гамильтоновых графов.
Проведенное доказательство справедливости достаточных признаков гамильтоновых графов было косвенным — мы не строили для данного произвольного графа, удовлетворяющего неравенству (5.5) или неравенству (5.6), гамильтоновых циклов.