Геометрические преобразования
Линейной комбинацией векторов  и
и  называется вектор
называется вектор  . При этом
числа
. При этом
числа  и
и  называются коэффициентами разложения вектора
называются коэффициентами разложения вектора  по векторам
по векторам  и
и  .
.
Если два вектора 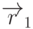 и
и 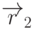 заданы своими координатами
заданы своими координатами 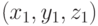 и
и 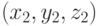 , то
операции над ними легко выразить через эти координаты:
, то
операции над ними легко выразить через эти координаты:


-
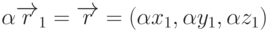 .
.
Векторы  ,
,  и
и  называются компланарными,
если они лежат в одной плоскости.
называются компланарными,
если они лежат в одной плоскости.
Векторы называются линейно независимыми, если равенство нулю их
линейной комбинации возможно только в случае равенства нулю
коэффициентов  и
и  .
.
Справедливы следующие свойства:
- Каковы бы ни были неколлинеарные векторы
 и
и  , для любого вектора
, для любого вектора  , лежащего в одной плоскости с ними, существуют числа
, лежащего в одной плоскости с ними, существуют числа  и
и  , такие, что
, такие, что  , причем такая пара чисел для каждого вектора единственная. Такое представление вектора
, причем такая пара чисел для каждого вектора единственная. Такое представление вектора  называется разложением по векторам
называется разложением по векторам  и
и  .
. - Каковы бы ни были некомпланарные векторы
 ,
,  и
и  , для любого вектора
, для любого вектора 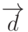 существуют числа
существуют числа  ,
,  и
и  , такие, что
, такие, что 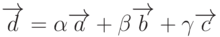 , причем эта тройка чисел для каждого вектора - единственная (разложение вектора
, причем эта тройка чисел для каждого вектора - единственная (разложение вектора 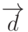 по векторам
по векторам  ).
). - Любые три вектора в системе координат плоскости являются линейно зависимыми.
- Любые четыре вектора в системе координат пространства являются линейно зависимыми.
Говорят, что пара линейно независимых векторов на плоскости (тройка линейно независимых векторов в пространстве) образуют базис, поскольку любой вектор может быть представлен в виде линейной комбинации этих векторов. Коэффициенты разложения вектора по базисным векторам называются координатами вектора в этом базисе. Если векторы базиса взаимно перпендикулярны и имеют единичную длину, то базис называется ортонормированным, а векторы базиса называются ортами. Таким образом, базис из единичных векторов, направленных вдоль осей декартовой системы координат, является ортонормированным.
Скалярным произведением векторов 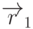 и
и 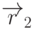 называется число, равное
произведению длин этих векторов на косинус угла между ними. Будем
обозначать скалярное произведение векторов символом
называется число, равное
произведению длин этих векторов на косинус угла между ними. Будем
обозначать скалярное произведение векторов символом  . Тогда скалярное
произведение можно выразить формулой
. Тогда скалярное
произведение можно выразить формулой

Несложно доказать следующие свойства данной операции.
- Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны.
- Если угол между двумя векторами острый, то скалярное произведение этих векторов положительно, если же угол тупой, то скалярное произведение отрицательно.
-
 (свойство коммутативности).
(свойство коммутативности). -
 (сочетательное относительно числового множителя свойство).
(сочетательное относительно числового множителя свойство). -
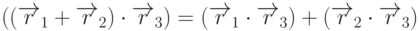 (распределительное относительно суммы векторов свойство).
(распределительное относительно суммы векторов свойство). - Скалярное произведение вектора самого на себя равно квадрату длины вектора.
Приведем некоторые формулы, связанные с разложением вектора в декартовой системе координат.
Пусть векторы 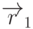 и
и 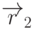 заданы своими координатами
заданы своими координатами  и
и  . Тогда их
скалярное произведение может быть вычислено по формуле
. Тогда их
скалярное произведение может быть вычислено по формуле
 |
( 3.1) |
Отсюда следует условие перпендикулярности векторов:
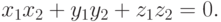
И, наконец, косинус угла между векторами вычисляется по формуле
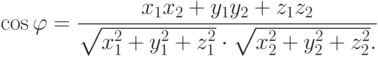 |
( 3.2) |
Теперь расстояние между двумя точками с координатами  и
и  можно
выразить через скалярное произведение соответствующих векторов:
можно
выразить через скалярное произведение соответствующих векторов:

Введем еще одно понятие, касающееся векторов. Три вектора
называются упорядоченной тройкой, если указано, какой из этих векторов
является первым, какой - вторым и какой - третьим. При записи тройки
векторов будем располагать эти векторы в порядке их следования. Так,
запись 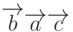 означает, что первым вектором тройки является вектор
означает, что первым вектором тройки является вектор  ,
вторым -
,
вторым -  , третьим -
, третьим -  .
.
Тройка векторов называется правой ( левой ), если после приведения к
общему началу вектор  располагается по ту сторону от плоскости,
содержащей векторы
располагается по ту сторону от плоскости,
содержащей векторы  ,
,  , откуда кратчайший поворот от
, откуда кратчайший поворот от  к
к  кажется совершающимся против часовой стрелки ( по часовой стрелке ).
кажется совершающимся против часовой стрелки ( по часовой стрелке ).
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  ,
обозначаемый символом
,
обозначаемый символом  и удовлетворяющий следующим требованиям:
и удовлетворяющий следующим требованиям:
- длина вектора
 равна произведению длин векторов
равна произведению длин векторов  ,
,  на синус угла между ними, т.е.
на синус угла между ними, т.е.
- вектор
 ортогонален векторам
ортогонален векторам  ,
,  ;
; - вектор
 направлен так, что тройка векторов
направлен так, что тройка векторов  является правой.
является правой.
Приведем (без доказательства) основные свойства векторного произведения.
-
![[\overrightarrow{a}\times\overrightarrow{b}]=-[\overrightarrow{b}\times\overrightarrow{a}]](/sites/default/files/tex_cache/75ec1f4601d6eef8988465c23633510f.png) (антисимметричность);
(антисимметричность); -
![\alpha[\overrightarrow{a}\times\overrightarrow{b}]=[\alpha\overrightarrow{a}\times\overrightarrow{b}]](/sites/default/files/tex_cache/ec8793dbdc155aeefb4eb94912749b2a.png) (сочетательное свойство относительно умножения на число);
(сочетательное свойство относительно умножения на число); -
![[(\overrightarrow{a}+\overrightarrow{b})\times\overrightarrow{c}]=[\overrightarrow{a}\times\overrightarrow{c}]+[\overrightarrow{b}\times\overrightarrow{c}]](/sites/default/files/tex_cache/b3c3ced5e8176c4d052779bca13b9939.png) (распределительное свойство относительно сложения);
(распределительное свойство относительно сложения); -
![[\overrightarrow{a}\times\overrightarrow{a}]=0](/sites/default/files/tex_cache/85aac29e4dfdcc2ba3b6d2c8a513298e.png) для любого вектора
для любого вектора  .
.
Ясно, что векторное произведение двух коллинеарных векторов дает
нулевой вектор. Выведем теперь формулy для векторного произведения.
Пусть базисные векторы декартовой системы координат 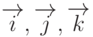 образуют правую
тройку. Тогда справедливы следующие соотношения:
образуют правую
тройку. Тогда справедливы следующие соотношения:
![\begin{gathered}
&[\overrightarrow{i}\times\overrightarrow{j}]=\overrightarrow{k}=-[\overrightarrow{j}\times\overrightarrow{i}], \quad
[\overrightarrow{j}\times\overrightarrow{k}]=\overrightarrow{i}=-[\overrightarrow{k}\times\overrightarrow{j}], \\
[\overrightarrow{k}\times\overrightarrow{i}]=\overrightarrow{j}=-[\overrightarrow{i}\times\overrightarrow{k}]
\end{gathered}](/sites/default/files/tex_cache/60a34c40df58c04dd1a69564ae3241aa.png)
Если заданы два вектора 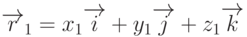 и
и  , то, учитывая свойства векторного
произведения, отсюда легко вывести, что
, то, учитывая свойства векторного
произведения, отсюда легко вывести, что
![\overrightarrow{r}_3=[\overrightarrow{r}_1\times\overrightarrow{r}_2]=x_3\overrightarrow{i}+y_3\overrightarrow{j}+z_3\overrightarrow{k},](/sites/default/files/tex_cache/0618987965e909143acdaedeea014b47.png)
 |
( 3.3) |

