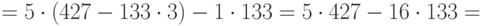|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Основы теории чисел
1.1.4 Алгоритм Евклида
Опишем способ нахождения наибольшего общего делителя, предложенный древнегреческим математиком Евклидом. Алгоритм Евклида применяется при решении многих задач, как теоретических, так и прикладных.
Алгоритм Евклида состоит в следующем. Сначала  делят на
делят на  (
( ). Если
). Если 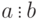 , то
, то 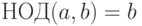 . В противном случае
. В противном случае  . Делим
. Делим  на
на 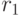 . Если
. Если  , то
, то 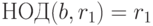 , но тогда и
, но тогда и  . Если
. Если  не делится на
не делится на 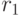 , то получится остаток
, то получится остаток 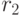 . Делим
. Делим 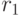 на
на 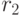 и т.д.
и т.д.
Остатки, получаемые в процессе деления, убывают и являются натуральными числами, значит, на некотором шаге получим деление без остатка.
Последний не равный нулю остаток является наибольшим общим делителем чисел  и
и  . Сформулируем это утверждение в виде теоремы.
. Сформулируем это утверждение в виде теоремы.
Теорема 1.3 Если
то 
Пример 1.2 Найдём 
Следствие 1.1 (Следствие из теоремы 1.3) Пусть  ,
,  , тогда существуют такие целые числа
, тогда существуют такие целые числа  и
и  , что
, что  . Другими словами, наибольший общий делитель двух чисел можно представить в виде линейной комбинации этих чисел с целыми коэффициентами.
. Другими словами, наибольший общий делитель двух чисел можно представить в виде линейной комбинации этих чисел с целыми коэффициентами.
Продолжение примера 1.2.
Из алгоритма Евклида вытекает существование наибольшего общего делителя для любых двух целых чисел  и
и  , кроме пары
, кроме пары 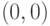 , для которой НОД не существует.
, для которой НОД не существует.
Теорема 1.4 Если 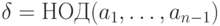 и
и 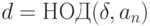 , то
, то 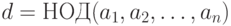 .
.
Отметим еще одно свойство НОД. Если каждое из чисел  и
и  умножить на одно и то же число
умножить на одно и то же число  , то их наибольший общий делитель умножится на
, то их наибольший общий делитель умножится на  .
.
1.1.5 Взаимно простые числа и их основные свойства
Определение 1.5 Если  , то числа
, то числа 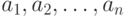 называются взаимно простыми.
называются взаимно простыми.
Например, числа 30 и 77 взаимно просты, а числа 30 и 72 не являются взаимно простыми, так как  .
.
Теорема 1.5 Для того, чтобы числа  и
и  были взаимно простыми, необходимо и достаточно, чтобы существовали такие целые числа
были взаимно простыми, необходимо и достаточно, чтобы существовали такие целые числа  и
и  , что
, что 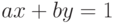 .
.
Следствие 1.2 Если числа  и
и  взаимно просты и
взаимно просты и  ,
,  , то числа
, то числа  и
и 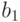 взаимно просты.
взаимно просты.
И еще одно свойство: частные от деления чисел  и
и  на
на  взаимно просты.
взаимно просты.
1.1.6 Наименьшее общее кратное
Определение 1.6 Пусть 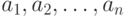 - целые числа, отличные от нуля. Целое число
- целые числа, отличные от нуля. Целое число  называется общим кратным этих чисел, если оно делится на каждое из данных чисел.
называется общим кратным этих чисел, если оно делится на каждое из данных чисел.
Например, произведение  - общее кратное всех своих сомножителей.
- общее кратное всех своих сомножителей.
Определение 1.7 Целое число  называется наименьшим общим кратным чисел
называется наименьшим общим кратным чисел 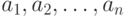 ,если оно является их общим кратным и при этом любое общее кратное этих чисел делится на
,если оно является их общим кратным и при этом любое общее кратное этих чисел делится на  .
.
Если наименьшее общее кратное существует, то оно определено с точностью до знака. Мы будем выбирать положительное значение наименьшего общего кратного и обозначать его так:

Имеет место важная теорема.
Теорема 1.6 Число  , где
, где  - наибольший общий делитель двух натуральных чисел
- наибольший общий делитель двух натуральных чисел  и
и  , является наименьшим общим кратным этих чисел.
, является наименьшим общим кратным этих чисел.
Рассмотрим основные свойства наименьшего общего кратного.
- Если каждое из чисел
 и
и  умножить на одно и то же число
умножить на одно и то же число  , то их НОК умножится на
, то их НОК умножится на  .
. - Если
 и
и  , то
, то

Пример 1.3 Найдем  .
.
Разделим каждое из данных чисел на  (очевидный делитель) и найдём
(очевидный делитель) и найдём 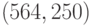 . Имеем:
. Имеем:

Тогда  .
.
Для нахождения НОК нескольких чисел имеет правило, аналогичное рассмотренному выше правилу нахождения НОД нескольких чисел.
Теорема 1.7 Если

то  .
.
Иными словами, для нахождения НОК чисел 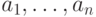 надо сначала найти
надо сначала найти  , потом
, потом  , и т.д. вплоть до
, и т.д. вплоть до 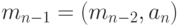 . На каждом шаге нам придется находить НОК двух чисел, а это мы уже умеем делать.
. На каждом шаге нам придется находить НОК двух чисел, а это мы уже умеем делать.
Пример 1.4 Найдем 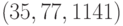 .
.
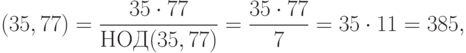

Ответ.  .
.
Теорема 1.8 НОК попарно взаимно простых чисел равно их произведению.
Пример 1.5 Найдём 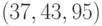 .
.
Имеем 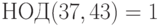 ,
, 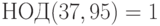 ,
, 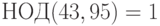 . Следовательно,
. Следовательно, 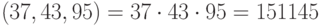 .
.


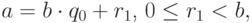

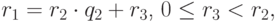

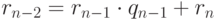 ,
, 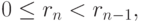


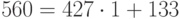
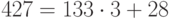

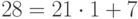
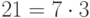 .
. .
.