Комбинаторика и числовые системы
Рассмотрим некоторые общие методы вычисления конечных сумм.
Самым простым прагматическим методом является поиск нужной суммы в справочниках "Сумм и интегралов" (человеческим опытом и знаниями нельзя пренебрегать!). Многие часто используемые суммы кем-то наверняка уже давно вычислены и предлагаются в этих справочниках.
Пример. Важные суммы из, например, известного справочника Двайта "Таблица сумм и интегралов":

Второй распространенный метод - угадывание закономерностей в суммируемых числах, вывод общей формулы для всех членов последовательности и затем - формулы для суммы, с последующим доказательством методом математической индукции справедливости этой формулы. Вышеприведенный пример мог бы служить иллюстрацией такого подхода, если бы мы доказали полученную формулу математической индукцией (предлагается выполнить эту несложную процедуру читателю), которая, собственно говоря, и была придумана для обоснования априорных предположений.
Третий метод можно назвать методом подбора подходящей рекуррентной зависимости. Он базируется на следующей теореме.
Теорема. Если для суммы вида
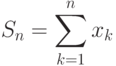
Пример. Вычислим сумму вида
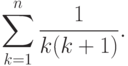
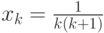 и, как легко это проверить, справедливо равенство
и, как легко это проверить, справедливо равенство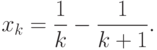
 для всех натуральных значений k. Тогда можно записать равенство вида
для всех натуральных значений k. Тогда можно записать равенство вида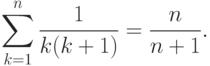
Сумма
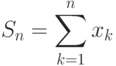
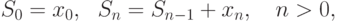
Есть и другие, достаточно сложные методы суммирования.
Аналогично знаку суммы вводится и знак произведения:
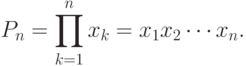
Пример. Факториал числа n>0 можно записать в виде

В математике часто используют ряд чисел, имеющих собственные имена в силу их исключительной важности. Примером такого числа является рассмотренное выше натуральное число (число Непера) e. Число  можно также отнести к таким числам. Рассмотрим некоторые другие важные числа.
можно также отнести к таким числам. Рассмотрим некоторые другие важные числа.
Числа Мерсенна - числа вида Mn=2n-1. Если n - не простое (например, кратно m, то есть n=km ), то эти числа - всегда не простые, так как в этом случае имеет место разложение (2km-1)=(2m-1)(2m(k-1)+2m(k-1)+ ...+1). Эти числа не всегда простые и в том случае, когда n - простое число.
Числа Ферма имеют вид: 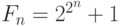 и предполагались самим Ферма (кстати, в письме к Мерсенну) простыми
и предполагались самим Ферма (кстати, в письме к Мерсенну) простыми 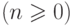 , но затем было доказано, что F5=4294967297 - не простое и делится, например, на 641.
, но затем было доказано, что F5=4294967297 - не простое и делится, например, на 641.
Числа Паскаля или треугольник Паскаля (проявление красоты и симметрии математических объектов):
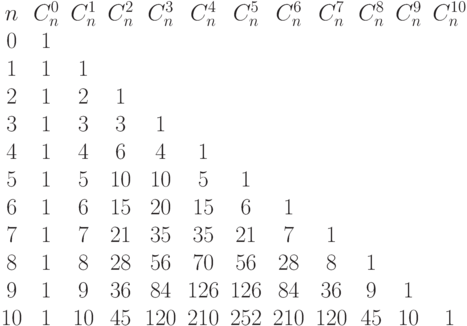
Числа Эйлера  (треугольник Эйлера), связывают обычные степени с биномиальными коэффициентами и удовлетворяют соотношениям:
(треугольник Эйлера), связывают обычные степени с биномиальными коэффициентами и удовлетворяют соотношениям:
![x^n =\sum\limits^n_{k=0} \langle C^k_n\rangle C^n_{x+k} , \quad n\ge 0, \\[3pt]
\langle C^k_n\rangle =(k+1) \langle C^k_{n-1}\rangle + (n-k)
C^{k-1}_{n-1}, \quad \langle C^0_0\rangle =1.](/sites/default/files/tex_cache/30e7c07729b66b9edd92c4c0de34879f.png)

Пример. Из треугольника Эйлера и приведенного выше рекуррентного соотношения получаем, в частности,
![x^2=C^2_x =C^2_{x+1}, \\[2pt]
x^3=C^3_x +4C^3_{x+1} + C^3_{x+2}, \\[2pt]
x^4 = C^4_x + 11 C^4_{x+1} +11C^4_x + C^4_{x+1} \ \ \text{и т.д.}](/sites/default/files/tex_cache/306306e1c2d02982fd8bf155ef1143c9.png)
В математике (особенно, в ее разделе - "теория чисел") рассматриваются и другие замечательные числа.
Немаловажным побудительным мотивом включения этого пункта у автора был эстетический. Поэтому, если у читателя при чтении этого очень небольшого раздела возник к рассматриваемым числам и аналогичным им интерес и получено удовольствие от красоты и симметрии формул, то цель пункта, по мнению автора, - достигнута.
