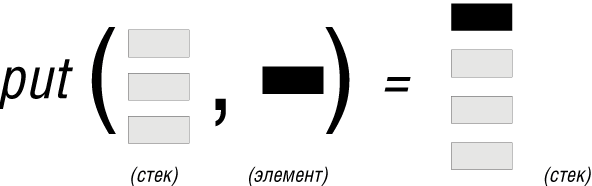Абстрактные типы данных (АТД)

Перечисление функций

Вслед за разделом ТИПЫ идет раздел ФУНКЦИИ, в котором перечисляются операции, применяемые к экземплярам данного АТД. Как уже говорилось, эти операции будут главными компонентами определения типа, с их помощью описывается, что могут предложить его экземпляры, а не то, чем они являются.

Ниже приведен раздел ФУНКЦИИ для абстрактного типа данных STACK. Если вы разработчик ПО, то этот стиль описания вам знаком: строки этого раздела напоминают декларации типизированных языков программирования таких, как Pascal или Ada. Строка для операции new похожа на объявление переменной, остальные - на заголовки процедур.

Функции

• put: STACK [G] x G -> STACK [G]
• 
• 
• empty: STACK [G] -> BOOLEAN
• new: STACK [G]

В каждой строке вводится определенная математическая функция, моделирующая соответствующую операцию над стеком. Например, функция put представляет операцию, которая вталкивает элемент на вершину стека.

Почему функции? Большая часть программистов не посчитает такую операцию как put функцией. Когда во время работы программной системы операция put применяется к стеку, она, как правило, изменяет этот стек, добавляя к нему элемент. Вследствие этого в приведенной выше классификации операций put была "командой" - операцией, которая может модифицировать объекты. (Две другие категории операций - это конструкторы и запросы).

Однако спецификация АТД - это математическая модель и в ее основании должны быть корректные математические методы. В математике понятие команды или, более общно, изменение чего-либо как таковое отсутствует: вычисление квадратного корня из числа 2 не изменяет само это число. Математические выражения просто определяют одни математические объекты в терминах некоторых других математических объектов. В отличие от вычисления программы на компьютере, они никогда не изменяют никакие математические объекты. Но поскольку мы нуждаемся в некотором математическом объекте для моделирования операций компьютера, то понятие функции представляется наиболее близким приближением. Функция - это механизм для получения некоторого результата, принадлежащего некоторому результирующему множеству, по любому допустимому входу, принадлежащему некоторому исходному множеству. Например, если R обозначает множество вещественных чисел, то определение функции

square_plus_one: R -> R
square_plus_one(x)= x2 + 1 (для каждого x из R)

вводит функцию square_plus_one, для которой R является и исходным и результирующим множеством и которая выдает для любого входа в качестве результата квадрат этого входа, увеличенный на 1.

Спецификации абстрактных типов данных используют именно это понятие. Например, операция put определяется как

put: STACK [G] x  G ->  STACK [G]

и означает, что put будет брать два аргумента: STACK экземпляров типа G и экземпляр типа G и возвращать в качестве результата новый STACK [G]. (Более формально, множеством определения функции put является множество STACK [G] _ G, являющееся декартовым произведением множеств STACK [G] и G, т.е. множеством пар <s, x>, в которых первый элемент s принадлежит STACK [G] , а второй элемент x принадлежит G.) Вот рисунок, иллюстрирующий это:

Рис. 6.3. Применение функции put

АТД имеют дело только с математическими функциями, у которых нет никаких побочных эффектов и которые, на самом деле, ничего не изменяют. Когда мы покинем утонченную сферу спецификации и попадем в неразбериху проектирования и реализации программ, нам придется восстановить понятие изменения, так как из-за накладных расходов мало кто одобрит программное окружение, в котором каждое выполнение операции "втолкнуть" в стек начинается с копирования этого стека. Мы рассмотрим позже переход от лишенного изменений мира АТД к полному изменений миру разработки ПО. Но поскольку сейчас мы хотим понять, как лучше всего определять типы, то математический взгляд на вещи нас вполне устраивает.

Из нашего обсуждения следуют роли операций, моделируемых каждой из функций спецификации STACK:

• Функция put возвращает новое состояние стека с одним новым элементом, помещенным на его вершину. Рисунок на предыдущей странице иллюстрирует операцию put(s, x), выполняемую над стеком s и элементом x.
• Функция remove возвращает новое состояние стека с вытолкнутым верхним элементом, если таковой был. Как и put, эта функция при проектировании и реализации должна превращаться в команду (операцию, изменяющую объект, обычно реализуемую как процедура). Мы увидим далее, как учесть возможность пустого стека, с вершины которого нечего удалять.
• Функция item возвращает верхний элемент стека, если таковой имеется.
• Функция empty выявляет пустоту стека, ее результатом является логическое значение (истина или ложь). Предполагается, что АТД BOOLEAN, задающий логические значения, определен отдельно.
• Функция new создает пустой стек.

В разделе ФУНКЦИИ эти функции определяются не полностью, вводятся только их сигнатуры - списки типов их аргументов и результата. Сигнатура функции put

STACK [G] x  G -> STACK [G]

показывает, что put берет в качестве аргумента пару вида <s,x>, в которой s - экземпляр типа STACK [G], а x - экземпляр типа G, и возвращает в качестве результата экземпляр типа STACK [G]. Вообще говоря, множество значений функции (его тип указывается в сигнатуре правее стрелки, здесь это STACK [G] ) может само быть декартовым произведением. Это можно использовать при описании операций, возвращающих два или более результатов.

В сигнатуре функций remove и item вместо обычной стрелки используется перечеркнутая стрелка . Это означает, что эти функции применимы не ко всем элементам множества входов. Описание функции new выглядит просто как

new: STACK

без всякой стрелки в сигнатуре. Фактически, это сокращение для записи

new: -> STACK,

определяющей функцию без аргументов. Здесь аргументы не нужны, поскольку new должна всегда возвращать один и тот же результат - пустой стек. Поэтому для простоты мы убрали здесь стрелку. Результат применения этой функции (т. е. пустой стек) будет записываться new, как сокращение для new(), обозначающего результат применения new к пустому списку аргументов.

Категории функций

В начале этой лекции операции над типами были разделены на конструкторы, запросы и команды. В спецификации АТД для нового типа T, например для STACK [G] в нашем примере можно определить эту классификацию более строго. Эта классификация просто проверяет, где по отношению к стрелке расположен в сигнатуре каждой функции тип T:

• Функция, в сигнатуре которой T появляется лишь справа от стрелки, например new, является функцией-конструктором. Она моделирует операцию, создающую экземпляры T из экземпляров других типов или вообще не использующую аргументов, например как в случае константного конструктора new.
• Такие функции как item и empty, у которых T появляется только слева от стрелки, являются функциями-запросами. Они моделируют операции, которые устанавливают свойства T, выраженные в терминах экземпляров других типов (в наших примерах - это BOOLEAN и параметр типа G ).
• Такие функции как put и remove, у которых T появляется с обеих сторон стрелки, являются функциями-командами. Они моделируют операции, которые по существующим экземплярам T и, возможно, экземплярам других типов выдают новые экземпляры типа T.