| Беларусь, Gomel |
Методы генерации признаков
11.3. Дискретное преобразование Фурье (ДПФ)
Преобразования типа Карунена-Лоева есть результат специальной обработки (оптимизации) применительно к конкретной выборке требует больших вычислительных затрат. Если разложить по некоторому заданному базису, то можно снизить затраты, правда снизив требования к разложению.
11.3.1. Одномерное дискретное преобразование Фурье
Пусть  –
–  исходных
измерений. Тогда ДПФ определяется следующим образом:
исходных
измерений. Тогда ДПФ определяется следующим образом:
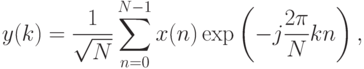
 и
и  .
.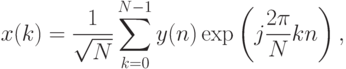

Определим
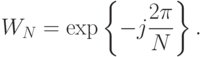
Тогда

Пусть 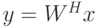 , тогда
, тогда 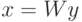 ,
,
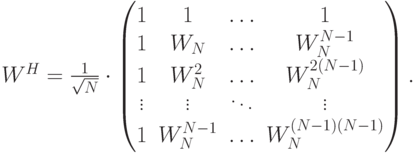
Утверждается, что  – унитарная симметрическая матрица.
Пусть
– унитарная симметрическая матрица.
Пусть 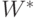 – сопряженная матрица:
– сопряженная матрица:  .
Тогда базисные вектора – это столбцы матрицы
.
Тогда базисные вектора – это столбцы матрицы  .
Таким образом, имеет место разложение по заданному базису (по
определению
.
Таким образом, имеет место разложение по заданному базису (по
определению 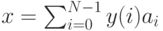 – разложение по базисным векторам).
– разложение по базисным векторам).
Прямое вычисление 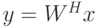 или
или 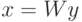 имеет сложность
имеет сложность  , однако, специфика структуры матрицы
, однако, специфика структуры матрицы  позволяет строить алгоритмы сложности
позволяет строить алгоритмы сложности 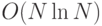 .
.
ДПФ можно рассматривать как разложение последовательности 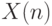 в
множество
в
множество  базисных последовательностей
базисных последовательностей 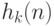 :
:
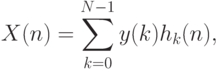
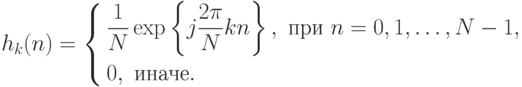
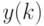 - коэффициенты разложения, а последовательности
- коэффициенты разложения, а последовательности 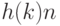 ортогональные:
ортогональные: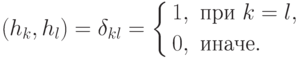
11.3.2. Двумерные ДПФ
Пусть 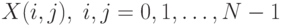 – двумерные измерения.
Тогда двумерное ДПФ есть:
– двумерные измерения.
Тогда двумерное ДПФ есть:
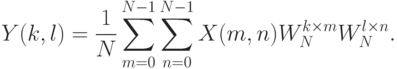
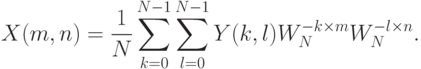
Данную запись компактно можно переписать в следующем виде:
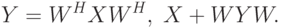
Данное преобразование – это преобразование с базисными матрицами
или образами 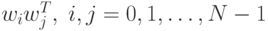 . Число
требуемых операций "в лоб" равно
. Число
требуемых операций "в лоб" равно 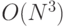 .
Учитывая специфическую структуру
.
Учитывая специфическую структуру  , существуют методы сложности
, существуют методы сложности 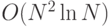 .
.
11.3.3. Дискретное косинусное преобразование (ДКП)
Данное преобразование имеет вид:
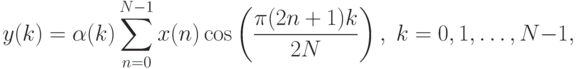
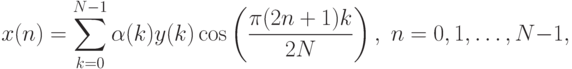
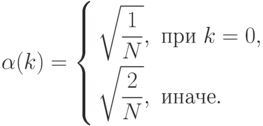 .
.Его можно переписать в векторной форме:  ,
где
,
где
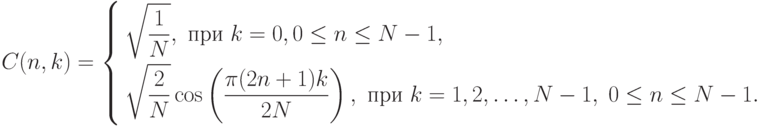
 – действительная матрица, причем
– действительная матрица, причем  .
.Двумерное ДПФ определяется так
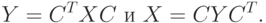
11.3.4. Дискретное синусное преобразования (ДСП)
Данное преобразование вычисляется аналогично косинусному через матрицу:
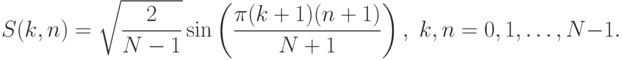
Вычислительная сложность затрат на ДКП и ДСП есть 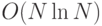 .
.
ДКП и ДСП обладают хорошими "упаковочными" свойствами для большинства изображений в том смысле, что концентрируют основную информацию в небольшом числе коэффициентов. Объясняется это тем, что оба они дают хорошее приближение для большого класса реальных образов, моделируемых случайных сигналов, известные как Марковский процесс 1-ого порядка.
