| Казахстан |
Градиентные алгоритмы обучения сети
Партан-методы
Для исправления недостатков наискорейшего спуска разработаны итерационный и модифицированный партан-методы.
Итерационный
партан-метод (  -партан) строится следующим образом. В
начальной точке
-партан) строится следующим образом. В
начальной точке 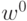 вычисляется градиент оценки
вычисляется градиент оценки  и
делается шаг
наискорейшего спуска - для этого используется одномерная оптимизация.
Далее снова вычисляется градиент
и
делается шаг
наискорейшего спуска - для этого используется одномерная оптимизация.
Далее снова вычисляется градиент  и выполняется спуск (т.е.
перемещение в
направлении антиградиента), и описанный процесс повторяется
и выполняется спуск (т.е.
перемещение в
направлении антиградиента), и описанный процесс повторяется  раз. После
раз. После  шагов наискорейшего спуска получаем точку
шагов наискорейшего спуска получаем точку 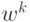 и
проводим одномерную
оптимизацию из
и
проводим одномерную
оптимизацию из 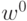 в направлении
в направлении 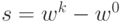 с
начальным шагом
с
начальным шагом 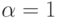 . После
этого цикл повторяется.
. После
этого цикл повторяется.
Модифицированный
партан-метод требует запоминания дополнительных
параметров. Он строится следующим образом. Из 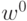 делается два
шага
наискорейшего спуска. Получаем
делается два
шага
наискорейшего спуска. Получаем 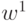 и
и  . Далее
выполняем одномерную
оптимизацию в направлении
. Далее
выполняем одномерную
оптимизацию в направлении  . Получаем
. Получаем 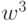 .
Далее выполняется
наискорейший спуск из
.
Далее выполняется
наискорейший спуск из 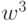 . Получаем
. Получаем 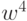 . Выполняем
одномерную оптимизацию из
. Выполняем
одномерную оптимизацию из  в направлении
в направлении  . Получаем
. Получаем 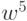 и~т.д. Таким образом, четные
и~т.д. Таким образом, четные 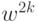 получаем наискорейшим спуском из
получаем наискорейшим спуском из  ,
нечетные
,
нечетные 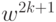 - одномерной
оптимизацией из
- одномерной
оптимизацией из  в направлении
в направлении 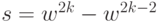 (начальный шаг
(начальный шаг 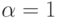 ).
Как показала практика, модифицированный партан-метод в задачах обучения
работает лучше, чем
).
Как показала практика, модифицированный партан-метод в задачах обучения
работает лучше, чем  -партан.
-партан.
Одношаговый квазиньютоновский метод и сопряженные градиенты
В тех случаях, когда является положительно определенной матрица  вторых производных оценки
вторых производных оценки  , наилучшим считается ньютоновское
направление
, наилучшим считается ньютоновское
направление
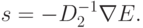
С использованием этой формулы квадратичные формы минимизируются за один шаг, однако, применять эту формулу трудно по следующим причинам:
- Время. Поиск всех вторых
производных функции
 и обращение матрицы
и обращение матрицы  требует больших вычислительных затрат.
требует больших вычислительных затрат. - Память. Для решения задач
большой размерности
 требуется хранить
требуется хранить 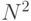 элементов матрицы
элементов матрицы 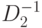 — это слишком
много.
— это слишком
много. - Матрица
 не всегда является положительно
определенной.
не всегда является положительно
определенной.
Для преодоления этих трудностей разработана масса методов. Идея квазиньютоновских методов с ограниченной памятью состоит в том, что поправка к направлению наискорейшего спуска отыскивается как результат действия матрицы малого ранга. Сама матрица не хранится, а её действие на векторы строится с помощью скалярных произведений на несколько специально подобранных векторов.
Простейший и весьма эффективный метод основан на 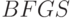 формуле
(Брайден-Флетчер-Гольдфард-Шанно) и использует результаты предыдущего
шага. Обозначим:
формуле
(Брайден-Флетчер-Гольдфард-Шанно) и использует результаты предыдущего
шага. Обозначим:
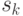 - направление спуска на
- направление спуска на  -шаге;
-шаге;
 - величина
- величина  шага (
шага (  -й шаг
- сдвиг на
-й шаг
- сдвиг на  );
);
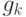 - градиент функции оценки в начальной точке
- градиент функции оценки в начальной точке  -го шага;
-го шага;
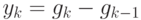 - изменение градиента в результате
- изменение градиента в результате  -го шага.
-го шага.
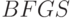 - формула для направления спуска на
- формула для направления спуска на  -м
шаге имеет вид:
-м
шаге имеет вид:
![\begin{align*}
s_{k+1} = - g_{k+1}+[(s_k,g_{k+1})y_k+(y_k,g_{k+1})s_k]/(y_k,s_k)-\\
- h_ks_k(s_k,g_{k+1})/(y_k,s_k) -
s_k(y_k,y_k)\cdot(s_k,g_{k+1})/(y_k,s_k)^2,
\end{align*}](/sites/default/files/tex_cache/365a448cb1a0f3873ffabee3a1791cc6.png)
где  - скалярное произведение векторов
- скалярное произведение векторов  и
и  .
.
Если одномерную оптимизацию в поиске шага проводить достаточно точно, то
новый градиент 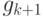 будет практически ортогонален предыдущему
направлению
спуска, т.е.
будет практически ортогонален предыдущему
направлению
спуска, т.е.  . При этом формула для
. При этом формула для 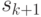 упрощается:
упрощается:
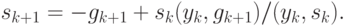
Это - формула метода сопряженных градиентов (МСГ), которому требуется достаточно аккуратная одномерная оптимизация при выборе шага.
В описанных методах предполагается, что начальное направление спуска  . После некоторой последовательности из
. После некоторой последовательности из  шагов
целесообразно
возвращаться к наискорейшему спуску - проводить рестарт. Он используется в
тех случаях, когда очередное
шагов
целесообразно
возвращаться к наискорейшему спуску - проводить рестарт. Он используется в
тех случаях, когда очередное 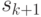 - плохое направление
спуска, т.е.
движение вдоль него приводит к слишком маленькому шагу либо вообще не дает
улучшения.
- плохое направление
спуска, т.е.
движение вдоль него приводит к слишком маленькому шагу либо вообще не дает
улучшения.
