|
Не обнаружил проекты, которые используются в примерах в лекции, также не увидел список задач. |
Классы
Операции над рациональными числами
Определим над рациональными числами стандартный набор операций - сложение и вычитание, умножение и деление. Реализуем эти операции методами с именами Plus, Minus, Mult, Divide соответственно. Поскольку рациональные числа - это прежде всего именно числа, то для выполнения операций над ними часто удобнее пользоваться привычными знаками операций ( +, -, *, / ). Язык C# допускает определение операций, заданных указанными символами. Этот процесс называется перегрузкой операций, и мы рассмотрим сейчас, как это делается. Конечно, можно было бы обойтись только перегруженными операциями, но мы приведем оба способа. Пользователь сам будет решать, какой из способов применять в конкретной ситуации - вызывать метод или операцию.
Покажем вначале реализацию метода Plus и операции +:
public Rational Plus(Rational a)
{
int u,v;
u = m*a.n +n*a.m; v= n*a.n;
return( new Rational(u, v));
}//Plus
public static Rational operator +(Rational r1, Rational r2)
{
return (r1.Plus(r2));
}Метод Plus реализуется просто. По правилам сложения дробей вычисляется числитель и знаменатель результата, и эти данные становятся аргументами конструктора, создающего требуемое рациональное число, которое удовлетворяет правилам класса.
Обратите внимание на то, как определяется операция класса. Именем соответствующего метода является сам знак операции, которому предшествует ключевое слово operator. Важно также помнить, что операция является статическим методом класса с атрибутом static.
В данном конкретном случае операция реализуется вызовом метода Plus. Как теперь все это работает? Вот пример:
public void TestPlusRational()
{
Rational r1=new Rational(0,0), r2 = new Rational(1,1);
Rational r3=new Rational(10,8), r4 = new Rational(2,6);
Rational r5=new Rational(4,-12), r6 = new Rational
(-12,-14);
Rational r7,r8, r9,r10, r11, r12;
r7 = r1.Plus(r2); r8 = r3.Plus(r4); r9 = r5.Plus(r6);
r10 = r1+r2; r11 = r3+r4; r12 = r5+r6+r10+r11;
r1.PrintRational("r1:(0,0)"); r2.PrintRational("r2:(1,1)");
r3.PrintRational("r3:(10,8)"); r4.PrintRational("r4:(2,6)");
r5.PrintRational("r5: (4,-12)"); r6.PrintRational
("r6: (-12,-14)");
r7.PrintRational("r7: (r1+r2)"); r8.PrintRational
("r8: (r3+r4)");
r9.PrintRational("r9: (r5+r6)"); r10.PrintRational
("r10: (r1+r2)");
r11.PrintRational("r11: (r3+r4)");
r12.PrintRational("r12: (r5+r6+r10+r11)");
}Обратите внимание на вычисление r12: здесь ощутимо видно преимущество операций, позволяющих записывать сложные выражения в простой форме. Результаты вычислений показаны на рис. 16.4.
Аналогичным образом определим остальные операции над рациональными числами:
public Rational Minus(Rational a)
{
int u,v;
u = m*a.n - n*a.m; v= n*a.n;
return( new Rational(u, v));
}//Minus
public static Rational operator -(Rational r1, Rational r2)
{
return (r1.Minus(r2));
}
public Rational Mult(Rational a)
{
int u,v;
u = m*a.m; v= n*a.n;
return( new Rational(u, v));
}//Mult
public static Rational operator *(Rational r1, Rational r2)
{
return (r1.Mult(r2));
}
public Rational Divide(Rational a)
{
int u,v;
u = m*a.n; v= n*a.m;
return( new Rational(u, v));
}//Divide
public static Rational operator /(Rational r1, Rational r2)
{
return (r1.Divide(r2));
}Вот тест, проверяющий работу этих операций:
public void TestOperRational()
{
Rational r1=new Rational(1,2), r2 = new Rational(1,3);
Rational r3, r4, r5, r6 ;
r3 = r1- r2; r4 = r1*r2; r5 = r1/r2; r6 = r3+r4*r5;
r1.PrintRational("r1: (1,2)"); r2.PrintRational("r2: (1,3)");
r3.PrintRational("r3: (r1-r2)"); r4.PrintRational("r4: (r1*r2)");
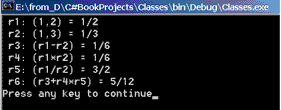
r5.PrintRational("r5: (r1/r2)");
r6.PrintRational("r6: (r3+r4*r5)");
}Результаты работы этого теста показаны на рис. 16.5. Обратите внимание: при перегрузке операций сохраняется общепринятый приоритет операций. Поэтому при вычислении выражения r3+r4*r5 вначале будет выполняться умножение рациональных чисел, а потом уже сложение.