| Россия, Таганрог, ИТА ЮФУ |
Контрастирование (редукция) нейронной сети
Показатели значимости для нейрона с дифференцируемым нелинейным элементом
Эти показатели ищутся почти так же как для сумматора. Пусть
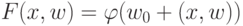
тогда

В евклидовой норме (что соответствует методу наименьших квадратов) получаем:
![\begin{align*}
\chi(x_i) =|w_i|[\sum_p(\varphi'(w_0+(x^p,w)))^2(x_i^p - M(x_i))^2]^{1/2},
\end{align*}](/sites/default/files/tex_cache/351e227e4c2f52d753b998ff61b310d2.png)
т.е. произведение модуля параметра 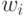 на среднеквадратичное
отклонение с
весами. Роль веса играет квадрат производной функции в точке
на среднеквадратичное
отклонение с
весами. Роль веса играет квадрат производной функции в точке 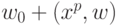 .
.
Показатели значимости для нейрона с пороговым нелинейным элементом (персептрона)
Эти показатели требуют для своего вычисления еще одного эвристического хода, т.к. прямо воспользоваться предыдущими формулами невозможно. Пусть функция, вычисляемая нейроном, имеет вид

Для каждого вектора данных 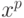 необходимо оценить значимость
изменения
аргумента функции
необходимо оценить значимость
изменения
аргумента функции  при замене
при замене  на
на 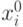 . Значение
. Значение  меняется только
тогда, когда
меняется только
тогда, когда  меняет знак, поэтому естественно оценивать
значимость
изменения
меняет знак, поэтому естественно оценивать
значимость
изменения  переменной
переменной  в масштабе,
определенном текущем значением
переменной, т.е. значимость
в масштабе,
определенном текущем значением
переменной, т.е. значимость  оценивается, как
оценивается, как  . Из этого
эвристического рассуждения получаем:
. Из этого
эвристического рассуждения получаем:

Если положить  и воспользоваться евклидовой
мерой, то вновь
получим произведение модуля параметров
и воспользоваться евклидовой
мерой, то вновь
получим произведение модуля параметров 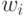 на среднеквадратичное
отклонение
с весом. В качестве весов выступают квадраты величин, обратных выходным
сигналам сумматоров:
на среднеквадратичное
отклонение
с весом. В качестве весов выступают квадраты величин, обратных выходным
сигналам сумматоров:
![\begin{align*}
\chi(x_i) =|w_i|\cdot [\sum_p (x_i^p - M(x_i))^2 /(w_0+(x^p,w))^2]^{1/2}.
\end{align*}](/sites/default/files/tex_cache/c49861e4d7594ff2812a53599b30ee53.png)
Полученные выражение для показателей значимости позволяют уп\-рощать основные элементы НС "снизу вверх", начиная с исключения самых малозначимых параметров.
