Самоорганизация (самообучение) нейронных сетей

Алгоритм Кохонена

Алгоритм Кохонена относится к наиболее старым алгоритмам обучения сетей с самоорганизацией на основе конкуренции, и в настоящее время существуют различные его версии. В классическом алгоритме Кохонена сеть инициализируется путем приписывания нейронам определенных позиций в пространстве и связывания их с соседями на постоянной основе. Такая сеть называется самоорганизующейся картой признаков (сеть SOFM - Self-Organizing Feature Map). В момент выбора победителя уточняются не только его веса, но также и веса его соседей, находящихся в ближайшей окрестности. Таким образом, нейрон-победитель подвергается адаптации вместе со своими соседями. В классическом алгоритме Кохонена функция соседства 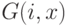определяется в виде

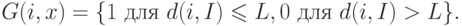
В этом выражении 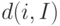обозначает эвклидово расстояние между векторами весов нейрона-победителя и -го нейрона. Коэффициент выступает в роли уровня соседства, его значение уменьшается в процессе обучения до нуля. Соседство такого рода называется прямоугольным.

Другой тип соседства, часто применяемый в картах Кохонена, - это соседство гауссовского типа, при котором функция 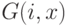задается формулой

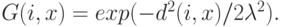
Степень адаптации нейронов-соседей определяется не только евклидовым расстоянием между -м нейроном и победителем ( -м нейроном), но также и уровнем соседства 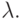В отличие от соседства прямоугольного типа, где каждый нейрон, находящийся в окрестности победителя, адаптировался в равной степени, при соседстве гауссовского типа уровень адаптации различен и зависит от значения функции Гаусса. Как правило, гауссовское соседство дает лучшие результаты обучения и обеспечивает лучшую организацию сети, чем прямоугольное соседство.

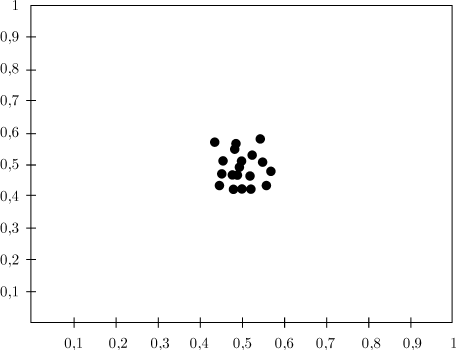
Самоорганизующаяся карта признаков проходит два этапа обучения. На первом этапе элементы упорядочиваются так, чтобы отражать пространство входных элементов, а на втором происходит уточнение их позиций. Как правило, процесс представляется визуально путем использования двумерных данных и построения соответствующей поверхности. Например, входные векторы выбираются случайным образом на основе однородного распределения в некотором квадрате, и начинается обучение карты. В определенные моменты в ходе обучения строятся изображения карты путем использования соответствия, показанного на рис. 1. Элементы соединяются линиями, чтобы показать их относительное размещение. Сначала карта выглядит сильно "измятой", но постепенно в ходе обучения она разворачивается и расправляется. Конечным результатом обучения является карта, покрывающая все входное пространство и являющаяся достаточно регулярной (т.е. элементы оказываются распределенными почти равномерно). Для примера была рассмотрена карта с топологией квадрата из 49 элементов, и для 250 точек данных, взятых из единичного квадрата, было проведено ее обучение, которое начиналось со случайного набора весовых значений, задающих размещение кластерных элементов в центре входного пространства, как показано на рис. 1. На рис. 2 и 3 иллюстрируется процесс разворачивания карты с течением времени. Как и для других типов сетей, в данном случае результат обучения зависит от учебных данных и выбора параметров обучения.

Рис. 1. Весовые векторы инициализируются случайными значениями из диапазона 0.4-0.6