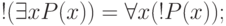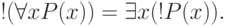Высказывания и предикаты
Расширение понятия предиката
В реальных программах далеко не все переменные имеют логический тип, что
означает невозможность их описания с помощью предикатов, введенных
определением 3.9. Так,
например, выражение 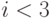 для
целочисленной переменной
для
целочисленной переменной  предикатом в смысле упомянутого
определения
заведомо не является, что плохо. Эти и некоторые другие причины побуждают
расширить множество предикатов, что и будет сейчас сделано в три этапа.
предикатом в смысле упомянутого
определения
заведомо не является, что плохо. Эти и некоторые другие причины побуждают
расширить множество предикатов, что и будет сейчас сделано в три этапа.
Определение 3.17.
Будем называть предикатом с переменными любых типов
выражение, которое может быть получено из предиката  (в смысле
определения 3.9 ) заменой
произвольного идентификатора
(в смысле
определения 3.9 ) заменой
произвольного идентификатора 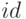 на любое заключенное в скобки выражение логического типа с переменными
различных типов. Вычисление значения получившегося предиката в произвольном
состоянии немедленно сводится к вычислению значения исходного предиката
на любое заключенное в скобки выражение логического типа с переменными
различных типов. Вычисление значения получившегося предиката в произвольном
состоянии немедленно сводится к вычислению значения исходного предиката  .
.
Начиная с этого момента выражение 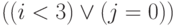 —
предикат, так как
для него можно указать следующую цепочку вывода:
—
предикат, так как
для него можно указать следующую цепочку вывода: 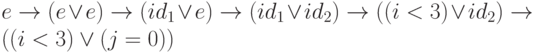 . Множеством состояний
этого
предиката является пространство
. Множеством состояний
этого
предиката является пространство 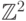 , так как каждая из
двух
входящих в него целых переменных может изменяться независимо от другой.
Если
, так как каждая из
двух
входящих в него целых переменных может изменяться независимо от другой.
Если  и
и  — программные переменные, то
пространство
— программные переменные, то
пространство 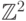 следует заменить на
следует заменить на  .
.
Примером предиката, который определен в состоянии, в котором одна из
входящих в него переменных не является определенной, может служить выражение 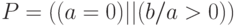 . В состоянии
. В состоянии 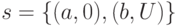 он истинен:
он истинен:  .
Подобные предикаты возникают при описании фрагментов программ типа
.
Подобные предикаты возникают при описании фрагментов программ типа
if (a==0 || b/a > 0) ...
Следующим шагом в направлении расширения понятия предиката будет
использование
кванторов существования  и всеобщности
и всеобщности 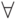 .
.
Если  — предикат в смысле определения 3.17, зависящий
от переменной
— предикат в смысле определения 3.17, зависящий
от переменной  произвольного типа, а
произвольного типа, а  —
некоторое множество, то будем
считать предикатами выражения
—
некоторое множество, то будем
считать предикатами выражения 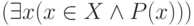 и
и 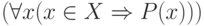 .
Первое из них означает, что существует хотя бы одно
.
Первое из них означает, что существует хотя бы одно 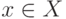 для которого выполнено
для которого выполнено  , а
второе — что для всех
, а
второе — что для всех 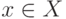 справедливо
справедливо  .
.
Часто вместо приведенных выше достаточно громоздких форм записи используют следующие более удобные, которые мы тоже будем считать допустимыми выражениями для предикатов.

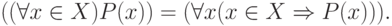
Когда используемое множество  понятно из контекста, его
опускают, что
приводит к выражениям
понятно из контекста, его
опускают, что
приводит к выражениям 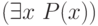 и
и 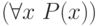 .
.
Кроме кванторов существования и всеобщности иногда используют еще один
квантор — квантор  ! существования и единственности,
который
может быть определен с помощью двух основных кванторов следующим образом:
! существования и единственности,
который
может быть определен с помощью двух основных кванторов следующим образом:
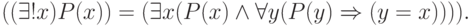
Использование кванторов в предикатах должно удовлетворять некоторым дополнительным ограничением. Связанным идентификатором будем называть идентификатор, непосредственно следующий в предикате за квантором, а свободным идентификатором — идентификатор, не являющийся связанным. Ограничение на использование кванторов в предикатах таково: в предикате один и тот же идентификатор не может быть как связанным, так и свободным, и, кроме того, идентификатор не может быть связан двумя различными кванторами.
В предикате 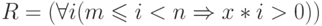 идентификатор
идентификатор  является связанным (квантором
является связанным (квантором 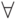 ), а идентификаторы
), а идентификаторы  ,
,  и
и  — свободными. Выражение
— свободными. Выражение  предикатом мы считать не можем,
ибо
предикатом мы считать не можем,
ибо  в нем является
одновременно и свободным идентификатором и связанным, что недопустимо. Его
легко слегка изменить так, чтобы оно стало предикатом:
в нем является
одновременно и свободным идентификатором и связанным, что недопустимо. Его
легко слегка изменить так, чтобы оно стало предикатом: 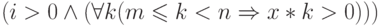 — уже предикат.
— уже предикат.
Третьим шагом в направлении расширения множества языка предикатов будет
ослабление требования на наличие в предикате всех тех скобок, которые
возникают в процессе его вывода. Напомним, что с точки зрения
определения 3.9 выражение 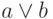 , например, предикатом не
является, что не слишком удобно с практической точки зрения.
, например, предикатом не
является, что не слишком удобно с практической точки зрения.
Разрешим удалять из предиката все те пары скобок, которые можно опустить без
потери его однозначного толкования. При этом семантика полученного предиката
определяется приоритетом операций: сначала вычисляются выражения внутри
скобок, затем — логические выражения, заменившие логические идентификаторы 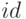 в смысле определения 3.17, после этого — кванторы
существования и всеобщности, а затем — логические операции
в смысле определения 3.17, после этого — кванторы
существования и всеобщности, а затем — логические операции 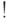 ,
,  и
и 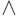 ,
, 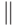 и
и 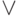 ,
,  и, наконец,
и, наконец,  .
.
Таким образом, мы принимаем следующее определение.
Определение 3.18. Будем называть предикатом в расширенном смысле предикат с переменными любых типов (см. определение 3.17 ), который может содержать кванторы и не иметь скобок, не являющимися необходимыми для его однозначного толкования.
Подробное описание приоритетов операторов в программах на языке Java приведено в следующей секции текущего параграфа, а пока совет — в случае сомнения всегда применяйте скобки для достижения нужного порядка вычисления выражения. Этот совет актуален и для программ и для предикатов.
Рассмотрим, как решаются типичные задачи на вычисление значения предикатов в расширенном смысле в различных состояниях.
Задача 3.4. Вычислите значения предикатов  и
и  в состоянии
в состоянии  .
.
Решение Если восстановить в этих предикатах все недостающие скобки, то мы получим
предикаты 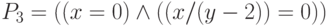 и
и 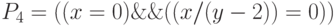 соответственно. В состоянии
соответственно. В состоянии  выражение
выражение  является
ложным, ибо
является
ложным, ибо  , а
, а 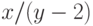 имеет значение
имеет значение  (не определено).
В соответствии с таблицами истинности для операций
(не определено).
В соответствии с таблицами истинности для операций 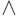 и
и  можно
сделать вывод, что
можно
сделать вывод, что  , а
, а  .
.
Задача 3.5. Вычислите значения предиката  в состоянии
в состоянии  .
.
Решение Предикат  представляет из себя конъюнкцию двух предикатов,
первый из
которых — это
представляет из себя конъюнкцию двух предикатов,
первый из
которых — это 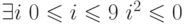 , а
второй в состоянии
, а
второй в состоянии  совпадает с
совпадает с 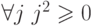 . Так как при
. Так как при  выполнено
выполнено 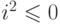 , то первый из них
истинен, а истинность
второго предиката не вызывает сомнений. Таким образом, предикат
, то первый из них
истинен, а истинность
второго предиката не вызывает сомнений. Таким образом, предикат 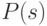 ,
являющийся конъюнкцией двух истинных выражений, сам является истинным, —
,
являющийся конъюнкцией двух истинных выражений, сам является истинным, —  .
.
Для дальнейшего нам полезно формализовать понятие подстановки, которое мы фактически уже неоднократно использовали для вычисления значения предиката в заданном состоянии.
Определение 3.19. Подстановкой 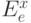 называется выражение, получающееся одновременной подстановкой
называется выражение, получающееся одновременной подстановкой  вместо всех
свободных вхождений
вместо всех
свободных вхождений  в
в  .
.
Вот несколько простых примеров: 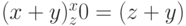 ;
для
;
для 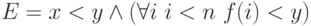 имеем
имеем 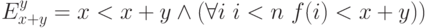 , но
, но 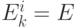 , так как
, так как  не
свободно в
не
свободно в  .
.
Для предикатов с кванторами справедливы дополнительные законы эквивалентности, называемые также правилами построения отрицания.
Предложение 3.16. Законы построения отрицания: