Все задачи курса
Схема вычисления инвариантной функции
При решении задач из этого раздела необходимо указать
множества  ,
,  и
и 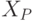 , функцию
, функцию  и преобразование
и преобразование  (см. определение инвариантной функции).
Должна быть объяснена программная реализация преобразования
(см. определение инвариантной функции).
Должна быть объяснена программная реализация преобразования  и
доказана правильность построенной программы вида "S0;while(e)S;S1;".
и
доказана правильность построенной программы вида "S0;while(e)S;S1;".
Задача 11.25. Напишите программу, находящую наибольший общий делитель 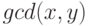 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Воспользуйтесь следующими свойствами наибольшего общего делителя
(не забудьте научиться доказывать все
эти свойства):
, не равных одновременно нулю.
Воспользуйтесь следующими свойствами наибольшего общего делителя
(не забудьте научиться доказывать все
эти свойства):
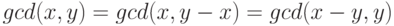 ,
,
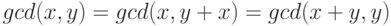 ,
,
 ,
,  ,
, 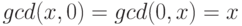 .
.
Задача 11.26. Напишите программу, перемножающую два целых числа, одно из
которых неотрицательно, без использования операции умножения. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить 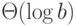 , таковы:
, таковы:  ,
, 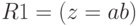 . При написании программы величины
. При написании программы величины  и
и  изменять не
разрешается. Воспользуйтесь тем, что
функция
изменять не
разрешается. Воспользуйтесь тем, что
функция  ,
,  является инвариантной
относительно преобразования
является инвариантной
относительно преобразования  , задаваемого
формулой
, задаваемого
формулой

Задача 11.27. Напишите программу, находящую наибольший общий делитель 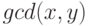 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Воспользуйтесь следующим свойством наибольшего общего
делителя (докажите его!):
, не равных одновременно нулю.
Воспользуйтесь следующим свойством наибольшего общего
делителя (докажите его!):

Здесь операция  позволяет найти остаток от деления
позволяет найти остаток от деления  на
на  .
.
Задача 11.28. Напишите программу, возводящую целое число в целую
неотрицательную степень. Точные
пред- и постусловия требуемой программы таковы:  ,
, 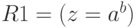 .
При написании программы величины
.
При написании программы величины  и
и  изменять не
разрешается. Воспользуйтесь тем, что
функция
изменять не
разрешается. Воспользуйтесь тем, что
функция  ,
, 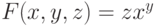 является инвариантной
относительно преобразования
является инвариантной
относительно преобразования  , задаваемого
формулой
, задаваемого
формулой  .
.
Задача 11.29. Напишите программу, находящую наибольший общий делитель 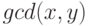 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Программа должна иметь временную сложность порядка
, не равных одновременно нулю.
Программа должна иметь временную сложность порядка  и не использовать операций деления и нахождения остатка от деления
(допустимо деление пополам, реализуемое с помощью операции сдвига).
Воспользуйтесь следующими свойствами наибольшего общего
делителя (докажите их!):
и не использовать операций деления и нахождения остатка от деления
(допустимо деление пополам, реализуемое с помощью операции сдвига).
Воспользуйтесь следующими свойствами наибольшего общего
делителя (докажите их!):
 ,
,  .
.
Указание
Воспользуйтесь инвариантностью функции 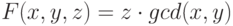 относительно
следующего преобразования
относительно
следующего преобразования  :
:

Не забудьте доказать  -инвариантность функции
-инвариантность функции  .
.
Задачи на индуктивные функции
При решении задач из этого раздела необходимо выяснить, является
ли индуктивной заданная функция  . В случае ее индуктивности
следует предъявить отображение
. В случае ее индуктивности
следует предъявить отображение  , иначе нужно построить
индуктивное
расширение
, иначе нужно построить
индуктивное
расширение  исходной функции и предъявить
исходной функции и предъявить  для
него. В последнем
случае нужно также указать отображение
для
него. В последнем
случае нужно также указать отображение  и исследовать
построенное
расширение на минимальность (минимальность не является обязательным
условием). Завершить решение следует написанием
программы, реализующей однопроходный алгоритм, с указанием соответствия
между программными переменными и
обозначениями, использованными в теоретической части решения. Необходимо
объяснить, как в программе реализуется вычисление
и исследовать
построенное
расширение на минимальность (минимальность не является обязательным
условием). Завершить решение следует написанием
программы, реализующей однопроходный алгоритм, с указанием соответствия
между программными переменными и
обозначениями, использованными в теоретической части решения. Необходимо
объяснить, как в программе реализуется вычисление  или
или  на пустой
(или ее заменяющей) цепочке, как именно реализовано перевычисление
функции при удлинении цепочки, и как находится
на пустой
(или ее заменяющей) цепочке, как именно реализовано перевычисление
функции при удлинении цепочки, и как находится  в
случае использования индуктивного расширения.
в
случае использования индуктивного расширения.
Задача 11.30. Напишите программу, определяющую значение в целой точке  многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
Задача 11.31. Напишите программу, вводящую последовательность целых чисел, и печатающую количество ее максимальных элементов.
Задача 11.32. Напишите программу, определяющую номер  первого элемента, равного
первого элемента, равного  , в
последовательности целых чисел. В том случае, если число
, в
последовательности целых чисел. В том случае, если число  в
последовательности не встречается, положите
в
последовательности не встречается, положите  равным нулю.
равным нулю.
Задача 11.33. Напишите программу, вводящую последовательность вещественных чисел, и печатающую среднее арифметическое ее элементов (для непустой последовательности).
Задача 11.34. Напишите программу, определяющую количество вхождений
образца  в последовательность символов.
в последовательность символов.
Задача 11.35. Напишите программу, определяющую количество минимальных элементов в последовательности неположительных целых чисел.
Указание В данном случае для доопределения индуктивного расширения на пустой цепочке нет необходимости использовать величины Integer.MIN_VALUE или Integer.MAX_VALUE.
Задача 11.36. Напишите программу, определяющую дисперсию не пустой последовательности
действительных чисел.
Дисперсией  последовательности
последовательности  называется
величина
называется
величина  , где
, где  — среднее арифметическое
элементов последовательности.
— среднее арифметическое
элементов последовательности.
Указание
Так как

то вводя обозначения 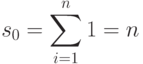 ,
,  ,
, 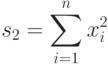 , получим
, получим  .
Легко проверить, что функция
.
Легко проверить, что функция 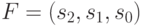 является индуктивной.
является индуктивной.
Задача 11.37. Напишите программу, определяющую значение в целой точке  многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
Задача 11.38. Напишите программу, определяющую значение в целой точке  производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
Указание
Продифференцировав по  равенство
равенство  и подставив затем
и подставив затем  , получите
соотношения
, получите
соотношения  и
и  , которые помогут построить
индуктивное расширение исходной функции.
, которые помогут построить
индуктивное расширение исходной функции.
Задача 11.39. Напишите программу, определяющую значение в целой точке  производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
Задача 11.40. Напишите программу, определяющую значение в целой точке  второй производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
второй производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
Задача 11.41. Напишите программу, определяющую правильность формулы над
алфавитом из четырех символов 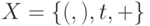 . Формула считается правильной,
если она может быть получена с помощью следующей НФБН:
. Формула считается правильной,
если она может быть получена с помощью следующей НФБН:  .
.
Указание
Рассмотрите следующее индуктивное расширение  функции
функции  , где
, где  ,
,  ,
, 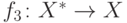 , определены следующим образом:
, определены следующим образом:
 может быть продолжена до правильной формулы,
может быть продолжена до правильной формулы,
 = разность числа левых и правых скобок в
= разность числа левых и правых скобок в  ,
,
 последний элемент
последний элемент  .
.
Задача 11.42. Напишите программу, определяющую номер  последнего элемента, равного
последнего элемента, равного  ,
в последовательности целых чисел. В том случае, если число
,
в последовательности целых чисел. В том случае, если число  в
последовательности не встречается, положите
в
последовательности не встречается, положите 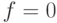 .
.
Задача 11.43. Напишите программу, определяющую число локальных максимумов в последовательности целых чисел. Элемент называется локальным максимумом, если у него нет соседа большего, чем он сам. Например, в любой одноэлементной последовательности всегда ровно один локальный максимум.
Задача 11.44. Напишите программу, определяющую среднюю длину связной возрастающей подпоследовательности в последовательности целых чисел.
Задача 11.45. Напишите программу (быстрое возведение в степень), возводящую целое число  в целую неотрицательную степень
в целую неотрицательную степень  , временная
сложность которой не должна превосходить
, временная
сложность которой не должна превосходить 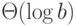 .
.
Указание
Рассмотрите эту функцию  , как функцию на пространстве последовательностей
над алфавитом
, как функцию на пространстве последовательностей
над алфавитом  . В качестве последовательности
. В качестве последовательности  нужно
взять инвертированное представление числа
нужно
взять инвертированное представление числа  в двоичной системе счисления.
Данная последовательность получается естественным образом —
последняя цифра числа
в двоичной системе счисления.
Данная последовательность получается естественным образом —
последняя цифра числа  есть "b&1", предпоследняя получается
по той же формуле после сдвига вправо ( "b>>>=1;" ) и так далее.
Индуктивное расширение
есть "b&1", предпоследняя получается
по той же формуле после сдвига вправо ( "b>>>=1;" ) и так далее.
Индуктивное расширение  исходной функции
исходной функции  легко находится, что и
позволяет написать требуемую программу.
легко находится, что и
позволяет написать требуемую программу.
Задача 11.46.
Напишите программу, определяющую количество вхождений
образца  в последовательность символов.
в последовательность символов.
Задача 11.47.
Напишите программу, определяющую значение в целой точке 
 -ой производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
-ой производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
