Tetromino

showTextScreen(), A Generic Text Screen Function

324. def showTextScreen(text):
325.     # This function displays large text in the
326.     # center of the screen until a key is pressed.
327.     # Draw the text drop shadow
328.     titleSurf, titleRect = makeTextObjs(text, BIGFONT, TEXTSHADOWCOLOR)
329.     titleRect.center = (int(WINDOWWIDTH / 2), int(WINDOWHEIGHT / 2))
330.     DISPLAYSURF.blit(titleSurf, titleRect)
331.
332.     # Draw the text
333.     titleSurf, titleRect = makeTextObjs(text, BIGFONT, TEXTCOLOR)
334.     titleRect.center = (int(WINDOWWIDTH / 2) - 3, int(WINDOWHEIGHT / 2) -
3)
335.     DISPLAYSURF.blit(titleSurf, titleRect)
336.
337.     # Draw the additional "Press a key to play." text.
338.     pressKeySurf, pressKeyRect = makeTextObjs('Press a key to play.',
BASICFONT, TEXTCOLOR)
339.     pressKeyRect.center = (int(WINDOWWIDTH / 2), int(WINDOWHEIGHT / 2) +
100)
340.     DISPLAYSURF.blit(pressKeySurf, pressKeyRect)

Instead of separate functions for the start screen and game over screens, we will create one generic function named showTextScreen(). The showTextScreen() function will draw whatever text we pass for the text parameter. Also, the text "Press a key to play." will be displayed in addition.

Notice that lines 328 to 330 draw the text in a darker shadow color first, and then lines 333 to 335 draw the same text again, except offset by 3 pixels to the left and 3 pixels upward. This creates a "drop shadow" effect that makes the text look a bit prettier. You can compare the difference by commenting out lines 328 to 330 to see the text without a drop shadow.

The showTextScreen() will be used for the start screen, the game over screen, and also for a pause screen (The pause screen is explained later in this chapter.)

342.     while checkForKeyPress() == None:
343.         pygame.display.update()
344.         FPSCLOCK.tick()

We want the text to stay on the screen until the user presses a key. This small loop will constantly call pygame.display.update() and FPSCLOCK.tick() until checkForKeyPress() returns a value other than None. This happens when the user presses a key.

The checkForQuit() Function

347. def checkForQuit():
348.     for event in pygame.event.get(QUIT): # get all the QUIT events
349.         terminate() # terminate if any QUIT events are present
350.     for event in pygame.event.get(KEYUP): # get all the KEYUP events
351.         if event.key == K_ESCAPE:
352.             terminate() # terminate if the KEYUP event was for the Esc key
353.         pygame.event.post(event) # put the other KEYUP event objects back

The checkForQuit() function can be called to handle any events that will cause the program to terminate. This happens if there are any QUIT events in the event queue (this is handle by lines 348 and 349), or if there is a KEYUP event of the Esc key. The player should be able to press the Esc key at any time to quit the program.

Because the pygame.event.get() call on line 350 pulls out all of the KEYUP events (including events for keys other than the Esc key), if the event is not for the Esc key, we want to put it back into the event queue by calling the pygame.event.post() function.

The calculateLevelAndFallFreq() Function

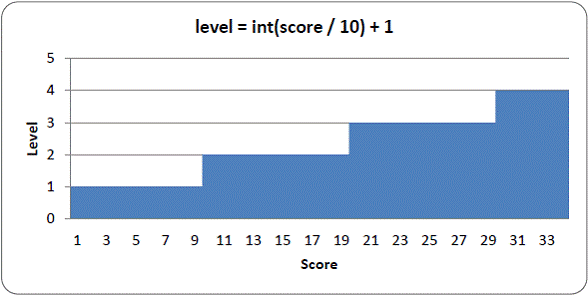
356. def calculateLevelAndFallFreq(score):
357.     # Based on the score, return the level the player is on and
358.     # how many seconds pass until a falling piece falls one space.
359.     level = int(score / 10) + 1
360.     fallFreq = 0.27 - (level * 0.02)
361.     return level, fallFreq

Every time the player completes a line, their score will increase by one point. Every ten points, the game goes up a level and the pieces start falling down faster. Both the level and the falling frequency can be calculated from the score that is passed to this function.

To calculate the level, we use the int() function to round down the score divided by 10. So if the score any number between 0 and 9, the int() call will round it down to 0. The + 1 part of the code is there because we want the first level to be level 1, not level 0. When the score reaches 10, then int(10 / 10) will evaluate to 1, and the + 1 will make the level 2. Here is a graph showing the values of level for the scores 1 to 34:

Рис. 7.6.

To calculate the falling frequency, we start with a base time of 0.27 (meaning that the piece will naturally fall once every 0.27 seconds). Then we multiply the level by 0.02, and subtract that from the 0.27 base time. So on level 1, we subtract 0.02 * 1 (that is, 0.02) from 0.27 to get 0.25. On level 2, we subtract 0.02 * 2 (that is, 0.04) to get 0.23. You can think of the level * 0.02 part of the equation as "for every level, the piece will fall 0.02 seconds faster than the previous level."

We can also make a graph showing how fast the pieces will fall at each level of the game:

Рис. 7.7.

You can see that at level 14, the falling frequency will be less than 0. This won’t cause any bugs with our code, because line 277 just checks that the elapsed time since the falling piece last fell one space is greater than the calculated falling frequency. So if the falling frequency is negative, then the condition on line 277 will always be True and the piece will fall on every iteration of the game loop. From level 14 and beyond, the piece cannot fall any faster.

If the FPS is set at 25, this means that at reaching level 14, the falling piece will fall 25 spaces a second. Considering that the board is only 20 spaces tall, that means the player will have less than a second to set each piece!

If you want the pieces to start (if you can see what I mean) falling faster at a slower rate, you can change the equation that the calculateLevelAndFallFreq() uses. For example, let’s say line 360 was this:

360.     fallFreq = 0.27 - (level * 0.01)

In the above case, the pieces would only fall 0.01 seconds faster on each level rather than 0.02 seconds faster. The graph would look like this (the original line is also in the graph in light grey):

Рис. 7.8.

As you can see, with this new equation, level 14 would only be as hard as the original level 7. You can change the game to be as difficult or easy as you like by changing the equations in calculateLevelAndFallFreq().

Generating Pieces with the getNewPiece() Function

363. def getNewPiece():
364.     # return a random new piece in a random rotation and color
365.     shape = random.choice(list(SHAPES.keys()))
366.     newPiece = {'shape': shape,
367.                 'rotation': random.randint(0, len(SHAPES[shape]) - 1),
368.                 'x': int(BOARDWIDTH / 2) - int(TEMPLATEWIDTH / 2),
369.                 'y': -2, # start it above the board (i.e. less than 0)
370.                 'color': random.randint(0, len(COLORS)-1)}
371.     return newPiece

The getNewPiece() function generates a random piece that is positioned at the top of the board. First, to randomly choose the shape of the piece, we create a list of all the possible shapes by calling list(SHAPES.keys()) on line 365. The keys() dictionary method returns a value of the data type "dict_keys", which must be converted to a list value with the list() function before being passed to random.choice(). This is because the random.choice() function only accepts list values for its parameter. The random.choice() function then randomly returns the value of an item from the list.

The piece data structures are simply a dictionary value with the keys 'shape', 'rotation', 'x', 'y' and 'color'.

The value for the 'rotation' key is a random integer between 0 to one less than however many possible rotations there are for that shape. The number of rotations for a shape can be found from the expression len(SHAPES[shape]).

Notice that we don’t store the list of string values (like the ones store in the constants like S_SHAPE_TEMPLATE) in each piece data structure to represent the boxes of each piece. Instead, we just store an index for the shape and rotation which refer to the PIECES constant.

The 'x' key’s value is always set to the middle of the board (also accounting for the width of the pieces themselves, which is found from our TEMPLATEWIDTH constant). The 'y' key’s value is always set to -2 to place it slightly above the board. (The top row of the board is row 0.)

Since the COLORS constant is a tuple of the different colors, selecting a random number from 0 to the length of COLORS (subtracting one) will give us a random index value for the piece’s color.

Once all of the values in the newPiece dictionary are set, the getNewPiece() function returns newPiece.

Adding Pieces to the Board Data Structure

374. def addToBoard(board, piece):
375.     # fill in the board based on piece's location, shape, and rotation
376.     for x in range(TEMPLATEWIDTH):
377.         for y in range(TEMPLATEHEIGHT):
378.             if SHAPES[piece['shape']][piece['rotation']][y][x] != BLANK:
379.                 board[x + piece['x']][y + piece['y']] = piece['color']

The board data structure is a data representation for the rectangular space where pieces that have previously landed are tracked. The currently falling piece is not marked on the board data structure. What the addToBoard() function does is takes a piece data structure and adds its boxes to the board data structure. This happens after a piece has landed.

The nested for loops on lines 376 and 377 go through every space in the piece data structure, and if it finds a box in the space (line 378), it adds it to the board (line 379).

Creating a New Board Data Structure

382. def getBlankBoard():
383.     # create and return a new blank board data structure
384.     board = []
385.     for i in range(BOARDWIDTH):
386.         board.append([BLANK] * BOARDHEIGHT)
387.     return board

The data structure used for the board is fairly simple: it’s a list of lists of values. If the value is the same as the value in BLANK, then it is an empty space. If the value is an integer, then it represents a box that is the color that the integer indexes in the COLORS constant list. That is, 0 is blue, 1 is green, 2 is red, and 3 is yellow.

In order to create a blank board, list replication is used to create the lists of BLANK values which represents a column. This is done on line 386. One of these lists is created for each of the columns in the board (this is what the for loop on line 385 does).

The isOnBoard() and isValidPosition() Functions

390. def isOnBoard(x, y):
391.     return x >= 0 and x < BOARDWIDTH and y < BOARDHEIGHT

The isOnBoard() is a simple function which checks that the XY coordinates that are passed represent valid values that exist on the board. As long as both the XY coordinates are not less 0 or greater than or equal to the BOARDWIDTH and BOARDHEIGHT constants, then the function returns True.

394. def isValidPosition(board, piece, adjX=0, adjY=0):
395.     # Return True if the piece is within the board and not colliding
396.     for x in range(TEMPLATEWIDTH):
397.         for y in range(TEMPLATEHEIGHT):
398.             isAboveBoard = y + piece['y'] + adjY < 0
399.             if isAboveBoard or
SHAPES[piece['shape']][piece['rotation']][y][x] == BLANK:
400.                 continue

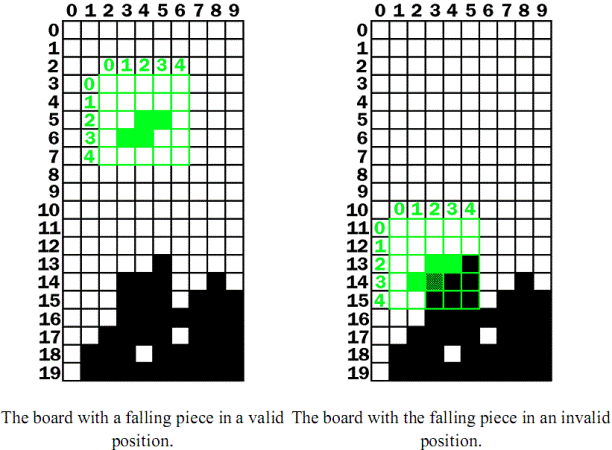
The isValidPosition() function is given a board data structure and a piece data structure, and returns True if all the boxes in the piece are both on the board and not overlapping any boxes on the board. This is done by taking the piece’s XY coordinates (which is really the coordinate of the upper right box on the 5x5 boxes for the piece) and adding the coordinate inside the piece data structure. Here’s a couple pictures to help illustrate this:

увеличить изображение
Рис. 7.9.

On the left board, the falling piece’s (that is, the top left corner of the falling piece’s) XY coordinates are (2, 3) on the board. But the boxes inside the falling piece’s coordinate system have their own coordinates. To find the "board" coordinates of these pieces, we just have to add the "board" coordinates of the falling piece’s top left box and the "piece" coordinates of the boxes.

On the left board, the falling piece’s boxes are at the following "piece" coordinates:

(2, 2) (3, 2) (1, 3) (2, 3)

When we add the (2, 3) coordinate (the piece’s coordinates on the board) to these coordinates, it looks like this:

(2 + 2, 2 + 3) (3 + 2, 2 + 3) (1 + 2, 3 + 3) (2 + 2, 3 + 3)

After adding the (2, 3) coordinate the boxes are at the following "board" coordinates:

(4, 5) (5, 5) (3, 6) (4, 6)

And now that we can figure out where the falling piece’s boxes are as board coordinates, we can see if they overlap with the landed boxes that are already on the board. The nested for loops on lines 396 and 397 go through each of the possible coordinates on the falling piece.

We want to check if a box of the falling piece is either off of the board or overlapping a box on the board. (Although one exception is if the box is above the board, which is where it could be when the falling piece just begins falling.) Line 398 creates a variable named isAboveBoard that is set to True if the box on the falling piece at the coordinates pointed to be x and y is above the board. Otherwise it is set to False.

The if statement on line 399 checks if the space on the piece is above the board or is blank. If either of those is True, then the code executes a continue statement and goes to the next iteration. (Note that the end of line 399 has [y][x] instead of [x][y]. This is because the coordinates in the PIECES data structure are reversed. See the previous section, "Setting Up the Piece Templates").

401.             if not isOnBoard(x + piece['x'] + adjX, y + piece['y'] +
adjY):
402.                 return False
403.             if board[x + piece['x'] + adjX][y + piece['y'] + adjY] !=
BLANK:
404.                 return False
405.     return True

The if statement on line 401 checks that the piece’s box is not located on the board. The if statement on line 403 checks that the board space the piece’s box is located is not blank. If either of these conditions are True, then the isValidPosition() function will return False. Notice that these if statements also adjust the coordinates for the adjX and adjY parameters that were passed in to the function.

If the code goes through the nested for loop and hasn’t found a reason to return False, then the position of the piece must be valid and so the function returns True on line 405.