Лекция 12: Сходимость последовательностей случайных величин
Теорема 34.
Пусть 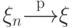 при
при 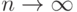 . Тогда для
сходимости
. Тогда для
сходимости 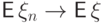 достаточно выполнения
любого из следующих условий:
достаточно выполнения
любого из следующих условий:
- Все члены последовательности ограничены одной и той же
постоянной:
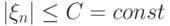 .
. - Все члены последовательности ограничены одной и той же
случайной
величиной с конечным первым моментом:
 ,
, 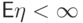
- Существует
 такое, что
такое, что 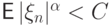 при всех
при всех  .
.
Самым слабым в этом списке является третье условие, наиболее ограничительным - первое. Ни одно из этих условий не является необходимым для сходимости математических ожиданий.
Сходимость по вероятности, так же как и любая другая сходимость, не портится под действием непрерывной функции.
Свойство 21. Пусть функция  действует из
действует из  в
в  .
.
- Если
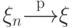 и функция
и функция  непрерывна,
то
непрерывна,
то 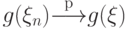 .
. - Если
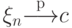 и
и  непрерывна
в точке
непрерывна
в точке  ,
то
,
то 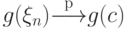 .
.
Доказательство. Простое доказательство первого утверждения можно предложить
в двух случаях, которыми мы и ограничимся:
если  (и тогда достаточно, чтобы
(и тогда достаточно, чтобы  была непрерывна в точке
была непрерывна в точке  ) или
если функция
) или
если функция  равномерно непрерывна.
равномерно непрерывна.
И в том и в другом случае для любого 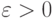 найдется
такое
найдется
такое 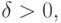 что для любого
что для любого  ,
удовлетворяющего
условию
,
удовлетворяющего
условию 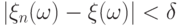 , выполняется
неравенство
, выполняется
неравенство 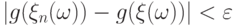 .
.
Другими словами, событие 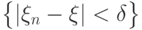 влечет за собой
событие
влечет за собой
событие 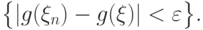 Следовательно, вероятность первого не больше вероятности второго.
Но, какое бы ни было
Следовательно, вероятность первого не больше вероятности второго.
Но, какое бы ни было 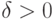 , вероятность первого события
стремится к единице по определению сходимости по вероятности:
, вероятность первого события
стремится к единице по определению сходимости по вероятности:
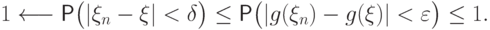
То же самое можно утверждать и для непрерывной функции многих переменных, примененной к нескольким сходящимся последовательностям.
Свойство 22.
Пусть функция  отображает
отображает  в
в  .
.
- Если
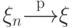 ,
, 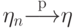 при
при 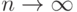 , функция
, функция 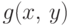 всюду непрерывна,
то
всюду непрерывна,
то 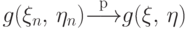 .
. - Если
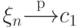 ,
, 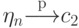 при
при 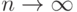 , функция
, функция  непрерывна в точке
непрерывна в точке 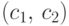 ,
то
,
то 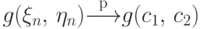 .
.
Доказательство. Докажем опять только второе свойство.
Воспользуемся определением непрерывности функции двух переменных:
для любого 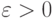 найдется
такое
найдется
такое 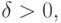 что для любого
что для любого  ,
принадлежащего
одновременно двум событиям
,
принадлежащего
одновременно двум событиям

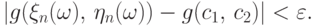
 влечет событие
влечет событие 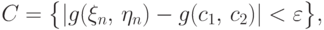 поэтому вероятность первого не больше вероятности второго.
Но вероятность пересечения двух событий, вероятности которых
стремятся к единице, также стремится к единице:
поэтому вероятность первого не больше вероятности второго.
Но вероятность пересечения двух событий, вероятности которых
стремятся к единице, также стремится к единице: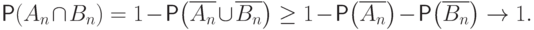
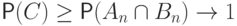 при
при 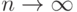 .
.Из свойства 22 вытекают
обычные свойства пределов,
хорошо знакомые нам по числовым последовательностям.
Например, функции 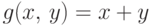 и
и 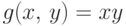 непрерывны в
непрерывны в  ,
поэтому предел суммы (произведения) сходящихся по вероятности
последовательностей равен сумме (произведению)
пределов.
,
поэтому предел суммы (произведения) сходящихся по вероятности
последовательностей равен сумме (произведению)
пределов.
Свойство 23.
Если 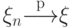 и
и 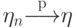 , то
, то 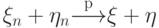 и
и 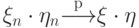 .
.
Сходимость "почти наверное" сильнее сходимости по вероятности.
Свойство 24.
Если 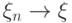 п.н., то
п.н., то 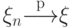 .
.
Доказательство.
Ограничимся для простоты случаем, когда 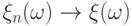 для любого
для любого  .
Зафиксируем
.
Зафиксируем 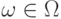 .
По определению предела,
.
По определению предела, 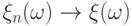 при
при 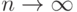 , если для всякого
, если для всякого 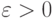 найдется
найдется 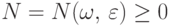 такое, что
для всех
такое, что
для всех  выполняется
неравенство
выполняется
неравенство 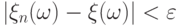 .
.
Событие 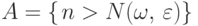 влечет
событие
влечет
событие 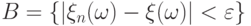 . Тогда
. Тогда
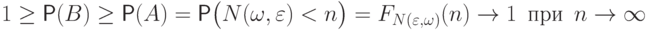
 , т.е.
, т.е. 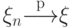 .
.