| Украина, kyiv |
Полнота исчисления предикатов
Переименование переменных
В этом разделе мы попытаемся аккуратно разобраться с простым
вопросом о том, почему и как можно переименовывать связанные
переменные, не меняя смысла формул. Мы уже видели, что формулы 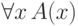 и
и 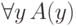 доказуемо
эквивалентны , то есть их эквивалентность доказуема в исчислении предикатов. Сейчас мы
хотим доказать общее утверждение об этом.
доказуемо
эквивалентны , то есть их эквивалентность доказуема в исчислении предикатов. Сейчас мы
хотим доказать общее утверждение об этом.
Корректная формулировка утверждения о переименовании переменных
требует осторожности. Например, нельзя сказать, что формула 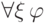 всегда эквивалентна
всегда эквивалентна 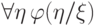 . Прежде всего, подстановка может
быть некорректной, как в случае формул
. Прежде всего, подстановка может
быть некорректной, как в случае формул

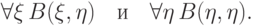
Нагляднее всего, видимо, сделать так. Давайте заключим в рамку все связанные вхождения всех переменных (в том числе вхождения после кванторов). После этого соединим линиями переменную после квантора и все ее вхождения, связанные именно этим вхождением квантора. Свободные вхождения переменных остаются при этом без рамок. Получится что-то вроде
Если после этого стереть переменные внутри рамок, получится схема формулы, которая содержит всю существенную информацию о ней. Будем называть две формулы подобными (отличающимися лишь именами связанных переменных), если они имеют одну и ту же схему.Теорема 52. (переименование связанных переменных) Подобные формулы доказуемо эквивалентны.
Докажем две простые леммы.
Лемма 1. Если формула  не содержит
переменной
не содержит
переменной  (ни связанно, ни свободно), то формулы
(ни связанно, ни свободно), то формулы
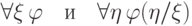
Доказательство. В самом деле, подстановка корректна, так как
в  нет кванторов по
нет кванторов по  . Поэтому выводима формула
. Поэтому выводима формула
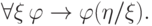
 , поэтому по правилу
Бернайса можно вывести
, поэтому по правилу
Бернайса можно вывести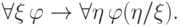
В обратную сторону:
подстановка  вместо
вместо  в формулу
в формулу  корректна (поскольку
корректна (поскольку  была подставлена вместо свободных
вхождений
была подставлена вместо свободных
вхождений  , при обратной подстановке
переменная
, при обратной подстановке
переменная  не попадет в область действия кванторов по ней) и дает формулу
не попадет в область действия кванторов по ней) и дает формулу  . Поэтому формула
. Поэтому формула
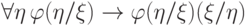
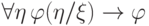
 свободно не входит (все свободные
вхождения были заменены на
свободно не входит (все свободные
вхождения были заменены на  ). Лемма 1 доказана.
). Лемма 1 доказана.Аналогичное утверждение для квантора существования доказывается точно так же.
Лемма 2. Замена подформулы на доказуемо эквивалентную дает доказуемо эквивалентную формулу.
Доказательство. Как мы видели, доказуемая эквивалентность
сохраняется после навешивания квантора: если 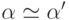 , то
, то 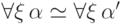 и
и  (символ
(символ  здесь обозначает доказуемую эквивалентность).
Кроме того, из
здесь обозначает доказуемую эквивалентность).
Кроме того, из 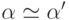 и
и 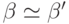 следует, что
следует, что 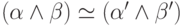 ,
, 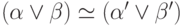 ,
, 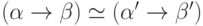 и
и 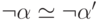 .
(В этом легко убедиться, написав подходящие пропозициональные
тавтологии.)
.
(В этом легко убедиться, написав подходящие пропозициональные
тавтологии.)
Теперь утверждение леммы легко доказать индукцией (начав с замененной подформулы и рассматривая все более длинные части формулы). Лемма 2 доказана.
Леммы 1 и 2 позволяют нам заменять переменные внутри рамок схемы на новые (ранее не использованные) переменные, получая доказуемо эквивалентную и подобную исходной формулу. Такими заменами можно из двух подобных формул получить третью, используя для замены одни и те же переменные. При этом обе исходные формулы доказуемо эквивалентны третьей, а значит, и друг другу.
(Использование третьей формулы существенно: мы не можем преобразовать первую формулу сразу во вторую, так как при замене переменных в рамках может не выполняться условие леммы 1.)
Аккуратное обращение со связанными и свободными переменными — традиционная головная боль авторов учебников по логике. Наиболее радикальный подход — вообще изгнать связанные переменные, заменив их квадратиками со связями между ними. Тогда при подстановке можно ни о чем не заботиться. Зато формулы перестают быть последовательностями символов, а становятся объектами со сложной структурой. (Этот подход использован в книге Бурбаки Теория множеств [3].)
Менее радикальный вариант состоит в том, чтобы разделить переменные на два типа — свободные и связанные. Так делается, например, в классической книге Гильберта и Бернайса Основания математики [8]. Тогда можно смело подставлять терм вместо свободной переменной, зато при навешивании квантора надо заменять свободную переменную на связанную.
Еще один вариант — договориться, что при подстановке терма вместо свободной переменных автоматически происходит переименование связанных переменных, создающих коллизии.
Все это, конечно, мелочи — но досадные, особенно если стремиться
к краткости, ясности и наглядности. Следы мучительных раздумий
на подобные темы видны в примечании книги Клини Математическая
логика [16]: "
Гильберт и Бернайс  и другие авторы
используют для обозначения свободных и связанных переменных
разные буквы
и другие авторы
используют для обозначения свободных и связанных переменных
разные буквы  Мы следовали этому правилу в
течение десятилетия
Мы следовали этому правилу в
течение десятилетия  Сейчас же мы твердо
убеждены, что использование единого списка переменных для
свободных и замкнутых вхождений дает небольшое, но
чувствительное преимущество".
Сейчас же мы твердо
убеждены, что использование единого списка переменных для
свободных и замкнутых вхождений дает небольшое, но
чувствительное преимущество".
С этим связан и другой выбор: как определять истинность формул. Тут есть две возможности: можно определять истинность формулы на оценке (при данных значениях параметров), а можно говорить только о замкнутых формулах, вводя константы для всех элементов интерпретации. И тот, и другой способы имеют недостатки, а выбор нами первого подхода — результат не единодушия авторов, а волевого решения.