НОУ ИНТУИТ | Языки и исчисления. Лекция 4: Контрпример

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2007 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Интуиционистская пропозициональная логика

Исключим из числа аксиом закон исключенного третьего ${A\lor\lnot A}$ . Полученное исчисление называется интуиционистским исчислением высказываний. (Обычное исчисление высказываний называют классическим, чтобы избежать путаницы при его сравнении с интуиционистским. Вообще математические рассуждения, опирающиеся на аксиому исключенного третьего, называют "классическими", а избегающие ее — "интуиционистскими".)

Конечно, сразу же возникают естественные вопросы. Почему именно эта аксиома вызывает сомнения? Вообще-то аксиом много, и можно было бы исключить любую и смотреть, что получится без нее — но ясно, что скорее всего получится что-то странное. Как понять, какие формулы останутся теоремами без закона исключенного третьего? Раньше у исчисления высказываний была "сверхзадача" — вывести все тавтологии и только их, а теперь?

Интуиционистская логика возникла как попытка (сделанная Гейтингом) формализовать (пусть частично) методы рассуждений, практикуемые в "интуиционистской математике". Голландский математик Брауэр широко известен как автор классической (во всех смыслах) теоремы Брауэра о неподвижной точке (она утверждает, что любое непрерывное отображение многомерного шара 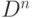D^n в себя имеет неподвижную точку). Но одновременно он создал целую школу в области оснований математики — математический интуиционизм. Отчего, спрашивал Брауэр, в теории множеств возникли парадоксы? Можно считать, что это оттого, что мы стали рассуждать о каких-то уж очень абстрактных объектах, которые существуют лишь в нашей (порой противоречивой) фантазии, так что следует проявлять осторожность и не подходить к опасной черте. Но Брауэр пошел дальше, говоря, что противоречия лишь симптом болезни, а надо устранить ее причину. Причину он видел в том, что математические рассуждения и понятия утратили интуитивный смысл, и нужно вернуться к основам и пересмотреть смысл самих логических связок.

Что мы имеем в виду (или должны иметь в виду), говоря о том, что мы установили, что " или "? Это значит, по Брауэру, что либо мы установили , либо установили . Когда мы устанавливаем, что " и ", это значит, что мы установили и , и . "Если , то " означает, что мы располагаем каким-то общим рассуждением, которое позволит нам установить , как только кто-то установит нам . Отрицание означает, что мы располагаем рассуждением, которое приводит к противоречию предположение, что установлено. 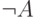(Как с точки зрения интуиционизма, так и с классической точки зрения, $\lnot A$ во всех смыслах эквивалентно 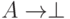$A\to\perp$ , где $\perp$ — заведомо ложное утверждение. Можно было бы вообще не использовать отрицания, а иметь константу $\perp$ — это не очень привычно, но технически удобно.)

Интуиционизм отвергает идею о том, что все высказывания делятся на истинные и ложные (пусть неизвестным нам образом). С этой точки зрения закон исключенного третьего совершенно безоснователен: $A\lor \lnot A$ означает, что для произвольного утверждения мы можем установить либо , либо его отрицание (то есть объяснить, почему в принципе не может быть установлено) — а почему, собственно?

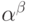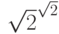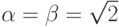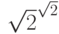Обычно, говоря об интуиционизме, приводят следующий пример рассуждения, неприемлемого с точки зрения интуиционизма. Докажем, что существуют иррациональные числа $\alpha$ и $\beta$ , для которых $\alpha^\beta$ рационально. В самом деле, рассмотрим два случая. Если $\sqrt{2}^{\sqrt{2}}$ рационально, то можно положить $\alpha\hm=\beta\hm=\sqrt{2}$ . 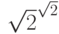Если же $\sqrt{2}^{\sqrt{2}}$ иррационально, то положим $\alpha=\sqrt{2}^{\sqrt{2}}$ и $\beta=\sqrt{2}$ ; легко проверить, что $\alpha^{\beta}=2$ . Интуиционист скажет, что это рассуждение некорректно: доказать существование чего-то означает построить этот объект, а мы так и не построили чисел $\alpha$ и $\beta$ , поскольку не установили, какой из двух случаев имеет место. (Заметим в скобках, что специалисты по алгебраической теории чисел знают, что $\sqrt{2}^{\sqrt{2}}$ иррационально и даже трансцендентно. 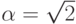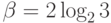Кроме того, не нужно быть специалистом, чтобы заметить, что можно положить $\alpha=\sqrt{2}$ и $\beta\hm=2\log_2 3$ .) Этот пример можно критиковать и с другой точки зрения, говоря, что само понятие действительного числа не является интуитивно ясным и требует обоснования.

Вообще интуиция — дело тонкое: если долго рассуждать, скажем, о действительных числах, то начинает казаться, что они в каком-то смысле существуют независимо от наших рассуждений. Именно поэтому психологически оправдан вопрос о том, скажем, как обстоят дела с континуум-гипотезой "на самом деле": существует ли несчетное множество действительных чисел, не равномощное всем действительным числам, или не существует?

Мы не будем говорить о философских предпосылках интуиционизма подробно. Вкратце упрощенная история вопроса такова. Брауэр наметил планы переустройства математики на интуиционистских принципах и отстаивал их настолько горячо, что однажды Гильберт в раздражении заметил: отменить закон исключенного третьего — это все равно что отнять у астрономов телескоп или запретить боксерам пользоваться кулаками. Но, продолжал он, никто не может изгнать математиков из рая, который создал Кантор.

В планы Брауэра не входила формализация интуиционистской логики и математики, скорее наоборот. Тем не менее анализ принципов интуиционизма пошел именно по этому пути, когда Гейтинг стал изучать пропозициональную логику без закона исключенного третьего. Различные спорные интуиционистские принципы стали предметом изучения с точки зрения формальной логики; были построены интуиционистские варианты формальной арифметики, теории множеств, логики предикатов, а также генценовские варианты интуиционистских систем. Были предложены различные интерпретации интуиционистской логики. Колмогоров предложил трактовать ее как "логику задач", Клини предложил понятие "реализуемости", использующее теорию алгоритмов для толкования формул; были предложены топологические модели для интуиционистской логики и т. д. В СССР знамя Брауэра подхватила школа Маркова, написав на нем, впрочем, "конструктивизм" вместо идеологически сомнительного "интуиционионизма" и более последовательно ограничиваясь конечными объектами. Крипке в 1960-е годы предложил некоторую семантику (определение истинности), согласованную с интуиционистским исчислением высказываний и весьма естественную (даже странно, что ее не придумали раньше); замечательным образом оказалось, что она в некотором смысле близка к методу форсинга, который примерно в это же время придумал Коэн, чтобы доказать независимость аксиомы выбора и континуум-гипотезы в теории множеств.

Возвращаясь к интуиционистскому исчислению высказываний, приведем несколько выводимых формул.

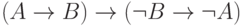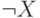Чтобы понять смысл формулы $(A\hm\to B)\hm\to (\lnot B\hm\to\lnot A)$ , вспомним, что отрицание $\lnot X$ можно толковать как 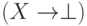$(X\to\perp)$ , где $\perp$ — заведомо ложное утверждение. Эта формула говорит, что если из следует , а из следует заведомо ложное утверждение, то из следует заведомо ложное утверждение (частный случай транзитивности отношения следования). Вывод ее не использует закона исключенного третьего. 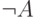В самом деле, по лемме о дедукции (доказательство которой остается тем же и для интуиционистского исчисления высказываний) достаточно доказать, что из $(A\to B)$ и $\lnot B$ выводится $\lnot A$ . 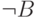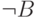Для этого, в свою очередь, достаточно доказать, что из $(A\to B)$ , $\lnot B$ и выводятся две противоречащие друг другу формулы (что очевидно: это формулы и $\lnot B$ ).
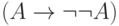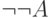Чтобы вывести формулу $(A\to\lnot\lnot A)$ , надо показать, что из выводится $\lnot\lnot A$ , для чего достаточно из и $\lnot A$ вывести две противоречащие друг другу формулы (что тривиально — годятся сами формулы и $\lnot A$ ).
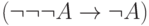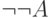Формула $(\lnot\lnot\lnot A\to \lnot A)$ получается из двух предыдущих: положим равным $\lnot\lnot A$ в первой из них.
Формула 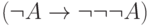$(\lnot A\to \lnot\lnot\lnot A)$ , с другой стороны, есть частный случай второй формулы, так что три отрицания равносильны одному.
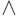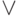Коммутативность и ассоциативность операций $\land$ и $\lor$ , так же как и два свойства дистрибутивности, не опирались на закон исключенного третьего.
По-прежнему 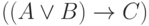$((A\lor B)\to C)$ равносильно 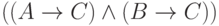$((A\to C)\hm\land(B\to C))$ (импликации в обе стороны, связывающие эти формулы, выводимы в интуиционистском исчислении высказываний).
Взяв $\perp$ в качестве в предыдущих формулах, мы видим, что один из законов Де Моргана (а именно, закон ${\lnot (A\lor B)\leftrightarrow\lnot A \land \lnot B}$ ) не опирается на закон исключенного третьего (что легко проверить и непосредственно).
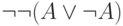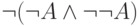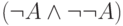Формулу $\lnot\lnot (A\lor \lnot A)$ сохранившийся закон де Моргана позволяет переписать в виде $\lnot (\lnot A \land \lnot\lnot A)$ , и нужно лишь вывести из $(\lnot A \land \lnot\lnot A)$ две противоположные формулы, что очевидно.