| Украина, Луганская обл., г. Рубежное |
Обход дерева. Перебор с возвратами
Разобьем задачу на две части: (1) обход произвольного дерева и (2) реализацию дерева допустимых позиций.
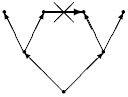
Сформулируем задачу обхода произвольного дерева. Будем считать, что у нас имеется Робот, который в каждый момент находится в одной из вершин дерева (вершины изображены на рисунке кружочками). Он умеет выполнять команды:
- вверх_налево (идти по самой левой из выходящих вверх стрелок)
- вправо (перейти в соседнюю справа вершину)
- вниз (спуститься вниз на один уровень)
(На рисунках стрелками показано, какие перемещения соответствуют этим командам.)
Кроме того, в репертуар Робота входят проверки (соответствующие возможности выполнить каждую из команд):
- есть_сверху ;
- есть_справа ;
- есть_снизу ;
(последняя проверка истинна всюду, кроме корня). Обратите внимание, что команда вправо позволяет перейти лишь к "родному брату", но не к "двоюродному".
Будем считать, что у Робота есть команда обработать и что его задача - обработать все листья (вершины, из которых нет стрелок вверх, то есть где условие есть_сверху ложно). Для нашей шахматной задачи команде обработать будет соответствовать проверка и печать позиции ферзей.
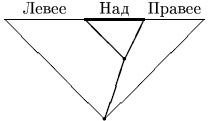
Доказательство правильности приводимой далее программы использует такие определения. Пусть фиксировано положение Робота в одной из вершин дерева. Тогда все листья дерева разбиваются на три категории: над Роботом, левее Робота и правее Робота. (Путь из корня в лист может проходить через вершину с Роботом, сворачивать влево, не доходя до нее и сворачивать вправо, не доходя до нее.) Через (ОЛ) обозначим условие "обработаны все листья левее Робота", а через (ОЛН) - условие " обработаны все листья левее и над Роботом".
Нам понадобится такая процедура:
procedure вверх_до_упора_и_обработать;
| {дано: (ОЛ), надо: (ОЛН)}
begin
| {инвариант: ОЛ}
| while есть_сверху do begin
| | вверх_налево;
| end
| {ОЛ, Робот в листе}
| обработать;
| {ОЛН}
end;дано: Робот в корне, листья не обработаны
надо: Робот в корне, листья обработаны
{ОЛ}
вверх_до_упора_и_обработать;
{инвариант: ОЛН}
while есть_снизу do begin
| if есть_справа then begin {ОЛН, есть справа}
| | вправо;
| | {ОЛ}
| | вверх_до_упора_и_обработать;
| end else begin
| | {ОЛН, не есть_справа, есть_снизу}
| | вниз;
| end;
end;
{ОЛН, Робот в корне => все листья обработаны}Осталось воспользоваться следующими свойствами команд Робота (в каждой строке в первой фигурной скобке записаны условия, в которых выполняется команда, во второй - утверждения о результате ее выполнения):
(1) { ОЛ, не есть_сверху } обработать { ОЛН }
(2) { ОЛ, есть_сверху } вверх_налево {ОЛ}
(3) { есть_справа ОЛН } вправо { ОЛ }
(4) {не есть_справа }, есть_снизу, ОЛН } вниз { ОЛН }
3.1.2.Доказать, что приведенная программа завершает работу (на любом конечном дереве).
Решение. Процедура вверх_до_упора_и_обработать } завершает работу (высота Робота не может увеличиваться бесконечно). Если программа работает бесконечно, то, поскольку листья не обрабатываются повторно, начиная с некоторого момента ни один лист не обрабатывается. А это возможно, только если Робот все время спускается вниз. Противоречие. (Об оценке числа действий см. далее.)
3.1.3.Доказать правильность следующей программы обхода дерева:
var state: (WL, WLU);
state := WL;
while есть_снизу or (state <> WLU) do begin
| if (state = WL) and есть_сверху then begin
| | вверх_налево;
| end else if (state = WL) and not есть_сверху then begin
| | обработать; state := WLU;
| end else if (state = WLU) and есть_справа then begin
| | вправо; state := WL;
| end else begin {state = WLU, not есть_справа, есть_снизу}
| | вниз;
| end;
end;
Доказательство завершения работы: переход из состояния ОЛ в ОЛН возможен только при обработке вершины, поэтому если программа работает бесконечно, то с некоторого момента значение state не меняется, что невозможно.