НОУ ИНТУИТ | Программирование на языке С++ в среде Qt Creator. Лекция 6: Статические и динамические матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 07.03.2015 | Уровень: для всех | Доступ: свободно | ВУЗ: Компания ALT Linux

Вам нравится? Нравится 77 студентам

| Поделиться |

Поддержать программу

6.5.2 Работа со строками и столбцами матрицы

Разработать программу на языке С++ для решения следующей задачи.

Задана матрица целых чисел 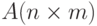$A(n\times m)$ . Сформировать массив , в который записать среднее арифметическое элементов каждого столбца заданной матрицы. Вывести номера строк матрицы, в которых находится более двух простых чисел.
Задана матрица вещественных чисел 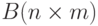$B(n \times m)$ . Сформировать массив , в который записать среднее геометрическое положительных элементов каждой строки заданной матрицы. Определить количество столбцов, упорядоченных по возрастанию.
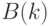Задана матрица целых чисел $A(n \times n)$ . Все простые числа, расположенные на побочной диагонали, заменить суммой цифр максимального элемента соответствующей строки матрицы. Сформировать массив , в который записать произведения элементов нечётных строк заданной матрицы.
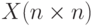В матрице целых чисел $X(n\times n)$ поменять местами диагональные элементы, упорядоченных по убыванию строк. Сформировать массив , в который записать суммы элементов чётных столбцов заданной матрицы.
Задана матрица целых чисел $A(n \times n)$ . Максимальный элемент каждого столбца заменить суммой цифр максимального элемента матрицы. Сформировать массив , в который записать количество чётных элементов в каждой строке заданной матрицы.
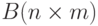Задана матрица целых чисел $B(n \times m)$ . Максимальный элемент каждого столбца заменить суммой цифр модуля минимального элемента матрицы. Сформировать массив , в который записать количество нечётных элементов в каждой строке заданной матрицы.
Задана матрица целых чисел $A(n \times n)$ . Сформировать массив из максимальных элементов столбцов заданной матрицы. Вывести индексы чиселпалиндромов, которые находятся на диагоналях матрицы.
Задана матрица вещественных чисел $P(n\times m)$ . Сформировать массив из номеров столбцов матрицы, в которых есть хотя бы один ноль. Найти строку с максимальной суммой элементов и поменять её с первой строкой.
Задана матрица вещественных чисел $C(k\times m)$ . Сформировать вектор из средних арифметических положительных значений строк матрицы, и вектор из номеров столбцов, которые представляют собой знакочередующийся ряд.
В каждом столбце матрицы вещественных чисел $P(k \times m)$ заменить минимальный элемент суммой положительных элементов этого же столбца. Сформировать вектор из номеров строк, представляющих собой знакочередующийся ряд.
В матрице целых чисел 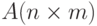$A(n\times m)$ обнулить строки, в которых более двух простых чисел. Сформировать массив из минимальных значений столбцов матрицы.
В матрице вещественных чисел $P(n \times m)$ найти и вывести номера столбцов, упорядоченных по убыванию элементов. Сформировать массив из максимальных значений строк матрицы.
В матрице вещественных чисел $D(n \times m)$ найти и вывести номера строк, упорядоченных по возрастанию элементов. Сформировать массив $C(m\times 2)$ из номеров минимальных и максимальных значений столбцов матрицы.
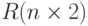В матрице вещественных чисел $P(n\times m)$ найти и вывести номера столбцов, упорядоченных по возрастанию. Сформировать вектор $R(n\times 2)$ из номеров минимальных и максимальных значений строк матрицы.
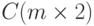В матрице вещественных чисел $D(n \times m)$ найти и вывести номера строк, упорядоченных по убыванию. Сформировать вектор $C(m \times 2)$ из максимальных и минимальных значений столбцов матрицы.
В матрице вещественных чисел 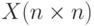$X(n \times n)$ найти максимальный и минимальный элементы. Поменять местами элементы строки с максимальным значением и элементы столбца с минимальным значением.
Задана матрица целых чисел $A(n \times n)$ . Сформировать массив , каждый элемент которого равен количеству положительных элементов с чётной суммой цифр в соответствующей строке матрицы. В столбцах матрицы поменять местами наибольший и наименьший элементы.
Задана матрица целых чисел $A(n \times m)$ . Сформировать массив , каждый элемент которого равен количеству положительных чисел с суммой цифр, кратной трём в соответствующем столбце матрицы. Найти строку с максимальным произведением элементов.
Задана матрица целых чисел 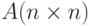$A(n\times n)$ . Все числа-палиндромы, расположенные на главной диагонали, заменить суммой цифр модуля минимального элемента соответствующего столбца матрицы. Сформировать вектор из произведений абсолютных ненулевых значений соответствующих строк матрицы.
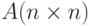Задана матрица целых чисел $A(n \times n)$ . Поменять местами элементы на диагоналях в столбцах, упорядоченных по возрастанию модулей. Сформировать вектор , каждый элемент которого равен сумме составных значений в соответствующей строке матрицы.
Задана матрица целых чисел $A(n\times n)$ . Минимальный элемент каждой строки заменить суммой цифр максимального простого элемента матрицы. Сформировать вектор , каждый элемент которого — среднее геометрическое ненулевых элементов в соответствующем столбце матрицы.
Задана матрица целых чисел $A(n \times n)$ . Максимальный элемент каждого столбца заменить суммой цифр минимального простого элемента матрицы. Сформировать вектор , каждый элемент которого равен количеству чётных элементов в соответствующей строке матрицы.
Задана матрица целых чисел $A(n \times n)$ . Обнулить строки, в которых на диагоналях нет чисел-палиндромов. Сформировать вектор , каждый элемент которого равен количеству нечётных элементов в соответствующем столбце матрицы.
Задана матрица вещественных чисел $P(n\times m)$ . Найти столбец с минимальным произведением элементов. Поменять местами элементы этого столбца и элементы последнего столбца. Сформировать вектор из сумм квадратов соответствующих строк матрицы.
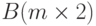Задана матрица целых чисел $A(n \times m)$ . В каждой строке заменить максимальный элемент суммой цифр минимального элемента этой же строки. Сформировать массив $B(m \times 2)$ , пара элементов которого равна соответственно количеству чётных и нечётных чисел в соответствующем столбце матрицы.

6.5.3 Решение задач линейной алгебры

Разработать программу на языке С++ для решения следующей задачи.

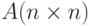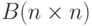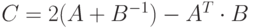Задана матрицы $A(n\times n)$ и $B(n\times n)$ . Вычислить матрицу $C=2(A+B^{-1})-A^T\cdot B$ .
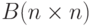Задан массив . Сформировать матрицы $A(n \times n)$ и $B(n \times n)$ по формулам: $A_{ij}=C_i\cdot C_j,\ B_{i,j}=\frac{A_{i,j}}{max(A)}$ .
Решить матричное уравнение , где — единичная матрица.
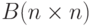Даны массивы и . Сформировать матрицы $A(n \times n)$ и $B(n \times n)$ по формулам: $A_{ij}=C_i\cdot D_j,\ B_{i,j}=\frac{A_{i,j}}{min(A)}$ .
Решить матричное уравнение , где — единичная матрица.
Квадратная матрица $A(n \times n)$ называется ортогональной, если $A^T = A^{-1}$ . Определить, является ли данная матрица ортогональной:
$\left(\begin{matrix}1&0.42&0.54&0.66\\0.42&1&0.32&0.44\\0.54&0.32&1&0.22\\0.66&0.44&0.22&1\end{matrix}\right).$
Для матрицы $H=E-\displaystyle\frac{vv^T}{\left|v\right|^2}$ , где — единичная матрица, а $v=\left[\begin{matrix}1\\0\\1\\1\end{matrix}\right]$ , проверить свойство ортогональности: $H^T=H^{-1}$ .
Проверить, образуют ли базис векторы
$f_1=\left[\begin{matrix}1\\-2\\1\\1\end{matrix}\right], f_2=\left[\begin{matrix}2\\-1\\1\\-1\end{matrix}\right], f_3=\left[\begin{matrix}5\\-2\\-3\\1\end{matrix}\right], f_4=\left[\begin{matrix}1\\-1\\1\\-1\end{matrix}\right].$

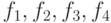Если образуют, то найти координаты вектора $x=[1\ -1\ 3\ -1]^T$ в этом базисе. Для решения задачи необходимо показать, что определитель матрицы со столбцами отличен от нуля, а затем вычислить координаты вектора в новом базисе по формуле $y=F^{-1}\cdot x$

.
Найти вектор как решение данной системы уравнений
$\left\{\begin{matrix} 3.75x_1-0.28x_2+0.17x_3=0.75\\ 2.11x_1-0.11x_2-0.12x_3=1.11\\ 0.22x_1-3.17x_2+1.81x_3=0.05. \end{matrix}\right.$
Вычислить модуль вектора .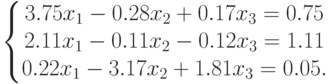
Вычислить скалярное произведение векторов и . Вектор $y = |1\ 1\ 2 - 3|$ , а вектор является решением СЛАУ: _
$\left\{\begin{matrix} 5.7x_1-7.8x_2-5.6x_3-8.3x_4=2.7\\ 6.6x_1+13.1x_2-6.3x_3+4.3x_4=-5.5\\ 14.7x_1-2.8x_2+5.6x_3-12.1x_4=8.6\\ 8.5x_1+12.7x_2-23.7x_3+5.7x_4=14.7. \end{matrix}\right.$
Вычислить вектор , решив СЛАУ
$\left\{\begin{matrix} 4.4x_1-2.5x_2+19.2x_3-10.8x_4=4.3\\ 5.5x_1-9.3x_2-14.2x_3+13.2x_4=6.8\\ 7.1x_1-11.5x_2+5.3x_3-6.7x_4=-1.8\\ 14.2x_1+23.4x_2-8.8x_3+5.3x_4=7.2. \end{matrix}\right.$
Найти $Y=X\cdot X^T$ .
Вычислить вектор , решив СЛАУ
$\left\{\begin{matrix}0.34x_1+0.71x_2+0.63x_3=2.08\\0.71x_1-0.65x_2-0.18x_3=0.17\\1.17x_1-2.35x_2+0.75x_3=1.28\end{matrix}\right.$
Найти модуль вектора .
Вычислить угол между векторами и . Вектор является решением СЛАУ:
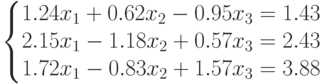
$\left\{\begin{matrix}1.24x_1+0.62x_2-0.95x_3=1.43\\2.15x_1-1.18x_2+0.57x_3=2.43\\1.72x_1-0.83x_2+1.57x_3=3.88\end{matrix}\right.$
.
Решив систему уравнений методом Гаусса:
$\left\{\begin{matrix}8.2x_1-3.2x_2+14.2x_3+14.8x_4=-8.4\\5.6x_1-12x_2+15x_3-6.4x_4=4.5\\5.7x_1+3.6x_2-12.4x_3-2.3x_4=3.3\\6.8x_1+13.2x_2-6.3x_3-8.7x_4=14.3\end{matrix}\right.$
Вычислить .
Решить СЛАУ 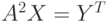, где $A=\left[\begin{matrix}2&1&5&2\\5&2&2&6\\2&2&1&2\\1&3&3&1\end{matrix}\right],\ Y=|3\ 1\ 2\ 1|$ |.
Решить СЛАУ , где $A=\left[\begin{matrix}2&1&5&2\\5&2&2&6\\2&2&1&2\\1&3&3&1\end{matrix}\right],\ Y=\left[\begin{matrix}3\\1\\2\\1\end{matrix}\right]$ .
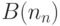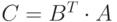Заданы матрицы и . Найти определитель матрицы $C=B^T\cdot A$ .
Задан массив . Сформировать матрицы и 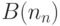по формулам: $A_{ij}=C_i\cdot C_j,\ B_{ij}=\frac{A_{ij}}{\sum\limits_{i=1}^nA_{ii}}$ . Найти определитель $|2E-A\cdot B|$ .
Для матрицы, где — единичная матрица, а
$P=\left[\begin{matrix}-26&-18&-27\\21&15&21\\12&8&13\end{matrix}\right]$
проверить свойство . При помощи метода Гаусса решить СЛАУ .
Квадратная матрица является симметричной, если для неё выполняется свойство . Проверить это свойство для матрицы
$\left(\begin{matrix} 1&0.42&0.54&0.66\\ 0.42&1&0.32&0.44\\ 0.54&0.32&1&0.22\\ 0.66&0.44&0.22&1 \end{matrix}\right)$
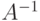. Вычислить $A^{-1}$ . Убедиться, что $A\cdot A^{-1}=E$ .
Ортогональная матрица обладает следующими свойствами:
- модуль определителя ортогональной матрицы равен 1;
- сумма квадратов элементов любого столбца ортогональной матрицы равна 1;
- сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна 0.
Проверить эти свойства для матриц:
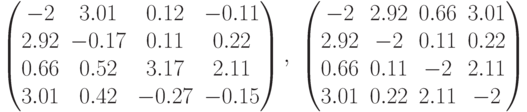
$\left(\begin{matrix}-2&3.01&0.12&-0.11\\2.92&-0.17&0.11&0.22\\0.66&0.52&3.17&2.11\\3.01&0.42&-0.27&-0.15\end{matrix}\right) ,\ \left(\begin{matrix}-2&2.92&0.66&3.01\\2.92&-2&0.11&0.22\\0.66&0.11&-2&2.11\\3.01&0.22&2.11&-2\end{matrix}\right)$
.
Проверить, образуют ли базис векторы
$f_1=\left[\begin{matrix}0.25\\0.333\\0.2\\0.1\end{matrix}\right],f_2=\left[\begin{matrix}0.33\\0.25\\0.167\\0.143\end{matrix}\right],f_3=\left[\begin{matrix}1.25\\-0.667\\2.2\\3.1\end{matrix}\right],f_4=\left[\begin{matrix}-0.667\\1.333\\1.25\\-0.75\end{matrix}\right] .$

Если образуют, то найти координаты вектора $x = [1\ 1\ 1\ 1]^T$ в этом базисе. Для решения задачи необходимо показать, что определитель матрицы F со столбцами 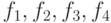отличен от нуля, а затем вычислить координаты вектора в новом базисе, решив СЛАУ $F\cdot y=x$ .
Решить СЛАУ:
$\left(\begin{matrix} 0.42&0.26&0.33&-0.22\\ 0.74&-0.55&0.28&-0.65\\ 0.88&0.42&-0.33&0.75\\ 0.92&0.82&-0.62&0.75 \end{matrix}\right)\cdot X=\left[\begin{matrix}1\\1\\1\\0\end{matrix}\right]$
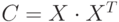Для матрицы $C=X\cdot X^T$ проверить условия ортогональности: $C\cdot C^T=E$ и $C^T\cdot C=E$ .
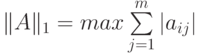Найти $\|A\|_1=max\sum\limits_{j=1}^m|a_{ij}|$ и $\|A\|_{11}=max\sum\limits_{i=1}^m|a_{ij}|$ для матрицы
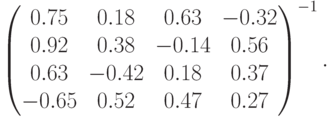
$\left(\begin{matrix} 0.75&0.18&0.63&-0.32\\ 0.92&0.38&-0.14&0.56\\ 0.63&-0.42&0.18&0.37\\ -0.65&0.52&0.47&0.27 \end{matrix}\right)^{-1} .$
Найти $\|A\|_{111}=\sqrt{\sum\limits_{i,j}a_{i,j}^2}$ для матрицы
$\left(\begin{matrix} -1.09&7.56&3.45&0.78\\ 3.33&4.45&-0.21&3.44\\ 2.33&-4.45&0.17&2.21\\ 4.03&1&3.05&0.11 \end{matrix}\right)^{-1}.$
Решить СЛАУ методом Гаусса
$\left\{\begin{matrix} 8.2x_1-3.2x_2+14.2x_3+14.8x_4&=-8.4\\ 5.6x_1-12x_2+15x_3-6.4x_4&=4.5\\ 5.7x_1+3.6x_2-12.4x_3-2.3x_4&=3.3\\ 6.8x_1+13.2x_2-6.3x_3-8.7x_4&=14.3 \end{matrix}\right.$
Выполнить проверку $A\cdot x=b$ .
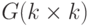Задан массив . Сформировать матрицы $B(k \times k)$ и $G(k \times k)$ по формулам
$B_{ij}=H_i\cdot H_j),\ G_{ij}=\displaystyle\frac{B_{ij}}{min(B)}.$

Решить матричное уравнение $G+E)\cdot X=5B^T-E$ , где — единичная матрица.

Дальше >>