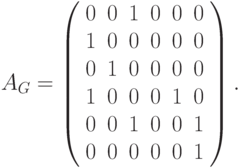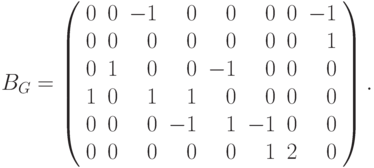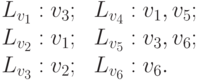НОУ ИНТУИТ | Основы дискретной математики. Лекция 9: Графы: представления, достижимость и связность

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 21.08.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Тверской государственный университет

Вам нравится? Нравится 37 студентам

| Поделиться |

Поддержать программу

Матрица (таблица) смежности

Определение 9.5. Матрицей смежности ориентированного (или неориентированного ) графа G=(V,E) с n вершинам и V= { v₁, ... , v_n} называется булева матрица A_G размера n x n с элементами

$a_{ij}= \left\{\begin{array}{ll} 1, & \textit{ если}\ \ (v_i,v_j) \in E\\ 0 & \textit{ в противном случае} \end{array} \right.$

Это представление позволяет легко проверять наличие ребер между заданными парами вершин. Для поиска всех соседей, в которые ведут ребра из вершины v_i, необходимо просмотреть соответствующую ей i -ю строку матрицы A_G, а чтобы найти вершины, из которых ребра идут в v_i, необходимо просмотреть ее i -ый столбец. Требуемая для A_G память - по порядку n² битов - не может быть уменьшена для графов, у которых "много" ребер. Но для разреженных графов с числом ребер существенно меньшим по порядку n² в матрице смежности много "ненужных" нулей. Для таких графов более эффективными могут оказаться другие представления.

Матрица (таблица) инцидентности

Определение 9.6. Матрицей инцидентности ориентированного (или неориентированного ) графа G=(V,E) с n вершинам и V= { v₁, ... , v_n} и m ребрами E={e₁, ..., e_m} называется матрица B_G размера n x m с элементами

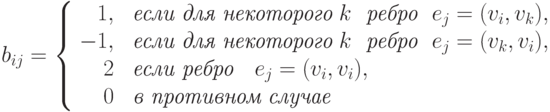
$b_{ij}= \left\{\begin{array}{rl} 1, & \textit{ если для некоторого}\ k \ \textit{ ребро }\ e_j= (v_i,v_k), \\ -1, & \textit{ если для некоторого}\ k \ \textit{ ребро }\ e_j= (v_k, v_i), \\ 2 & \textit{ если ребро }\ \ e_j= (v_i, v_i), \\ 0 & \textit{ в противном случае} \end{array} \right.$

Таким образом, в матрице инцидентности B_G любому ребру e_j = (v_i,v_k) соответствует j -ый столбец, в котором в i -ой строке стоит 1, а в k -ой - -1. Ребра -петли выделяются числом 2. Для проверки наличия ребра между двумя вершинам и v_i и v_k требуется просмотреть i -ю и k -ую строки B_G, поиск всех соседей вершины требует просмотра соответствующей строки. Если m >> n, то это требует существенно больше времени, чем при использовании матрицы смежности. Поэтому при практическом решении задач на графах матрица инцидентности почти не используется.

Списки смежности

Определение 9.7. Пусть G=(V,E) - ориентированный граф, v - вершина из V. Список смежности L_v для вершины v включает все смежные с ней вершины, т.е.

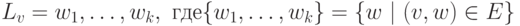
$L_v = w_1, \ldots , w_k ,\ где \{w_1, \ldots , w_k\} = \{ w\ |\ (v,w) \in E\}$

Представление графа G=(V,E) c n вершинам и V= { v₁, ... , v_n} с помощью списков смежности состоит из списков смежности всех вершин: L_v1, L_v2, ... , L_vn.

Размер этого представления сравним с суммой числа вершин и ребер графа. Оно позволяет легко переходить по ребрам от вершины к ее соседям. В программах списки смежности представляются списковыми структурами, которые легко реализуются во всех языках программирования.

Пример 9.1. Рассмотрим следующий граф G=(V,E):

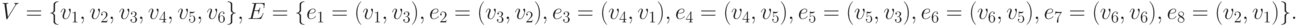
$V= \{ v_1, v_2, v_3, v_4, v_5, v_6\}, \\ E = \{ e_1=(v_1, v_3), e_2= (v_3, v_2), e_3 =(v_4, v_1), e_4= (v_4, v_5), \\e_5 = (v_5, v_3), e_6= (v_6, v_5), e_7=(v_6, v_6) , e_8= (v_2, v_1)\}.$

Он показан на рис. 9.2.

Построим для него определенные выше представления.

Матрица смежности.
$A_G = \left( \begin{array}{cccccc} 0 & 0 & 1 & 0& 0& 0\\ 1 & 0 & 0 & 0& 0& 0\\ 0 & 1 & 0 & 0& 0& 0\\ 1 & 0 & 0 & 0& 1& 0\\ 0 & 0 & 1 & 0& 0& 1\\ 0 & 0 & 0 & 0& 0& 1 \end{array}\right).$
Матрица инцидентности.
$B_G = \left( \begin{array}{rrrrrrrr} 0 & 0 & -1 & 0& 0& 0 & 0& -1\\ 0 & 0 & 0 & 0& 0& 0&0 & 1\\ 0 & 1 & 0 & 0& -1& 0& 0&0\\ 1 & 0 & 1 & 1& 0& 0 &0 &0 \\ 0 & 0 & 0 & -1& 1& -1 & 0& 0\\ 0 & 0 & 0 & 0& 0& 1 &2 & 0 \end{array}\right).$
Списки смежности.
$\begin{array}{ll} L_{v_1}: v_3; & \ L_{v_4}: v_1, v_5;\\ L_{v_2}: v_1; & \ L_{v_5}: v_3, v_6;\\ L_{v_3}: v_2; & \ L_{v_6}: v_6. \end{array}$